Ulteriori informazioni sulle disuguaglianze polinomiali

Questa calcolatrice può aiutarvi a risolvere le disequazioni polinomiali, mostrandovi tutte le fasi del processo di calcolo della soluzione e fornendovi un grafico della disequazione che rappresenta la soluzione

La disuguaglianza fornita può essere qualcosa di semplice come "x^2 > 1", oppure qualcosa di più complesso come "x^3 + 3x^2 + 3x + 1 > 0".

Una volta fornita una disuguaglianza polinomiale valida, fare clic sul pulsante "Calcola" per ottenere la soluzione e tutti i passaggi indicati.

Si tenga presente che non tutti i polinomi forniti si prestano a soluzioni esatte. Più basso è il grado del polinomio, più è probabile che si trovi una soluzione esatta alla disequazione.

Cos'è una disuguaglianza polinomiale

Una disuguaglianza polinomiale è semplicemente un tipo di disuguaglianza in cui le espressioni coinvolte sono polinomiali e nessuno dei suoi termini è un'espressione non polinomiale. Per esempio

\[\displaystyle \frac{1}{2} x^2 + \frac{3}{4} < \displaystyle \frac{x^3}{3} \]

è una disuguaglianza polinomiale, mentre

\[\displaystyle \frac{1}{2} x^2 + \frac{3}{4} < \sin(x) \]

è un no, a causa della presenza del termine \(\sin x\), che non è un polinomio. Risolvere le disuguaglianze in generale è un processo difficile, ma per quelli polinomiali abbiamo un piano d'azione chiaro.

Come si risolve una disuguaglianza polinomiale

• Passo 1: Assicurarsi che tutti i termini siano polinomi. In caso contrario, i metodi specifici utilizzati per i polinomi potrebbero non essere applicabili
• Passo 2: Mettere tutto da una parte, lasciando zero dall'altra
• Passaggio 3: Sostituendo il segno di disuguaglianza con "=", risolvere l'equazione associata (si tratta di trovare gli zeri di un polinomio)
• Passaggio 4: Raccogliere tutti i punti critici della disuguaglianza, che in questo caso sono gli zeri reali dell'ausiliare Equazione polinomiale (in questo caso non si considerano le radici complesse)
• Passaggio 5: Se non esistono punti critici, significa che l'espressione non cambia segno, quindi l'intera retta reale sarà una soluzione, altrimenti non c'è soluzione. Per verificare, scegliete un punto qualsiasi e vedete se soddisfa la disuguaglianza: se lo soddisfa, l'intera retta reale è la soluzione, altrimenti non c'è soluzione
• Passaggio 6: Se ci sono punti critici, costruire intervalli con punti critici consecutivi (usando -∞ come punto critico iniziale e ∞ come punto critico finale)
• Passaggio 7: Controllare ciascuno di questi intervalli e vedere se un punto all'interno soddisfa la disuguaglianza. In caso affermativo, l'intervallo fa parte della soluzione, altrimenti non fa parte della soluzione.

L'idea chiave è che i punti critici e gli intervalli che ne derivano sono intervalli per i quali l'espressione non cambia segno, quindi o l'intero intervallo è una soluzione o nessun punto dell'intervallo fa parte della soluzione.

Zeri e punti critici dei polinomi

Uno dei motivi per cui è possibile risolvere le disequazioni polinomiali è che è relativamente semplice analizzare le espressioni polinomiali per i punti critici, oltre al fatto che i polinomi sono espressioni continue.

Ci saranno disuguaglianze come

\[\displaystyle \frac{\sin(x^2-1)}{x^3-1} < 1 \]

in cui sarà molto più difficile trovare punti critici. disuguaglianze lineari sono ancora più semplici per trovare i punti critici, ma questo è tutto. Qualsiasi disuguaglianza generale presenta le sue complessità.

Applicazioni dei polinomi nella vita reale

Le applicazioni dei polinomi sono numerose. Per esempio, in Fisica, quando si studia la cinematica, ci sono alcune interessanti espressioni polinomiali derivate dalle leggi di Newton. Queste espressioni possono definire le condizioni per la posizione di un corpo, il che potrebbe portare a una disuguaglianza polinomiale per determinare quali volte il corpo si trova al di sopra di una certa altezza, il che potrebbe rivelarsi cruciale, ad esempio, nella balistica.

Inoltre, quando si studiano le equazioni differenziali, si possono trovare nell'equazione dei termini di scarico che dipendono da una potenza e hanno una struttura polinomiale, per i quali si possono usare alcune disuguaglianze avanzate, come le disuguaglianze di Gronwall.

Esempio: risolvere disuguaglianze polinomiali

Risolvere: \(x^2 - x > \frac{1}{2}\)

Soluzione: Dobbiamo innanzitutto risolvere la seguente equazione quadratica \(\displaystyle x^2-x-\frac{1}{2}=0\):

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{1 \pm \sqrt{\left(-1\right)^2-4\left(1\right)\left(-\frac{1}{2}\right)}}{2\cdot 1} = \displaystyle \frac{1 \pm \sqrt{3}}{2}\]

allora, troviamo che:

\[ {x}_1 = \frac{1}{2}-\frac{1}{2}\sqrt{3}=-\frac{1}{2}\sqrt{3}+\frac{1}{2} \] \[{x}_2 = \frac{1}{2}+\frac{1}{2}\sqrt{3}=\frac{1}{2}\sqrt{3}+\frac{1}{2}\]

Analisi dei punti critici

L'elenco dei punti critici trovati è organizzato in ordine crescente: \(-\frac{1}{2}\sqrt{3}+\frac{1}{2}\), \(\frac{1}{2}\sqrt{3}+\frac{1}{2}\).

Su questa base, dobbiamo analizzare i seguenti intervalli:

- Per l'intervallo \(\left(-\infty, -\frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\): il lato sinistro è positivo, quindi \(\left(-\infty, -\frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) fa parte della soluzione.

- Per l'intervallo \(\left(-\frac{1}{2}\sqrt{3}+\frac{1}{2}, \frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\): il lato sinistro è negativo, il che significa che \(\left(-\frac{1}{2}\sqrt{3}+\frac{1}{2}, \frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) non fa parte della soluzione.

- Per l'intervallo \(\left(\frac{1}{2}\sqrt{3}+\frac{1}{2}, \infty\right)\): il lato sinistro è positivo, il che significa che \(\left(\frac{1}{2}\sqrt{3}+\frac{1}{2}, \infty\right)\) fa parte della soluzione.

Soluzione alla disuguaglianza

In base alla disuguaglianza fornita e analizzando i punti critici, troviamo che la soluzione della disuguaglianza è: \(x < -\frac{1}{2}\sqrt{3}+\frac{1}{2}\) o \(x > \frac{1}{2}\sqrt{3}+\frac{1}{2}\).

Utilizzando la notazione per intervalli, la soluzione si scrive come:

\[\left(-\infty,-\frac{1}{2}\sqrt{3}+\frac{1}{2}\right) \cup \left(\frac{1}{2}\sqrt{3}+\frac{1}{2},\infty\right)\]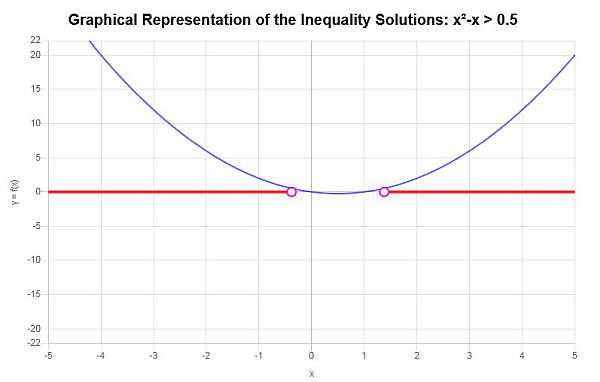

che conclude il calcolo.

Esempio: polinomio di grado superiore

Risolvere la seguente disuguaglianza: \(x^3 - x > 1\)

Soluzione:

Per risolvere \(x^3-x > 1\) mettiamo prima tutto da una parte:

\[x^3-x-1> 0\]

Ora, da ciò si ottiene l'equazione associata che deve essere risolta per prima, che è \(x^3-x-1=0\). Osserviamo che il grado è \(\displaystyle deg(p) = 3\), il coefficiente primo è \(\displaystyle a_{3} = 1\) e il coefficiente costante è \(\displaystyle a_0 = -1\).

Tentativo di radici razionali

Cercheremo prima di tutto di trovare radici razionali semplici, con il Teorema dello zero razionale.

Il compito successivo è quello di trovare i numeri interi che dividono il coefficiente principale \(a_{3}\) e il coefficiente costante \(a_0\), che verranno utilizzati per costruire i nostri candidati zeri dell'equazione polinomiale.

i divisori di \(a_{3} = 1\) sono: \(\pm 1\).

i divisori di \(a_0 = -1\) sono: \(\pm 1\).

Pertanto, dividendo ogni divisore del coefficiente costante \(a_0 = -1\) per ogni divisore del coefficiente principale \(a_{3} = 1\), troviamo il seguente elenco di candidati ad essere radici:

\[\pm \frac{ 1}{ 1}\]

Ora, tutti i candidati devono essere testati per vedere se sono una soluzione. Quanto segue si ottiene testando ogni candidato:

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle -1^3-\left(-1\right)-1 & = & \displaystyle -1 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle 1^3-1-1 & = & \displaystyle -1 \ne 0 \\\\ \end{array}\]

Ma poiché non abbiamo trovato alcuna radice razionale mediante ispezione, non possiamo continuare con la fattorizzazione utilizzando metodi elementari, quindi il processo si ferma qui.

OPZIONALE : Si tratta di un polinomio di grado \(3\), per il quale esistono un totale di \(3\) radici, anche se alcune potrebbero essere complesse, ma in questo caso sono state trovate meno di \(3\) soluzioni con metodi elementari.

Utilizzando metodi avanzati di equazione cubica, si può scoprire che l'insieme completo delle soluzioni è:

\[x_1=\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\]
\[x_2=\frac{\frac{1}{6}\cdot \left(-3i\sqrt{3}\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-3\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}+i\sqrt{3}-1\right)}{\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}}\]
\[x_3=\frac{\frac{1}{6}\cdot \left(3i\sqrt{3}\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-3\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-i\sqrt{3}-1\right)}{\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}}\]

Analisi dei punti critici

L'unico punto critico trovato è \(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\).

Su questa base, dobbiamo analizzare i seguenti intervalli:

- Per l'intervallo \(\left(-\infty, \left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\right)\): il lato sinistro è negativo, quindi \(\left(-\infty, \left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\right)\) non fa parte della soluzione.

- Per l'intervallo \(\left(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}, \infty\right)\): il lato sinistro è positivo, il che implica che \(\left(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}, \infty\right)\) fa parte della soluzione.

Soluzione alla disuguaglianza

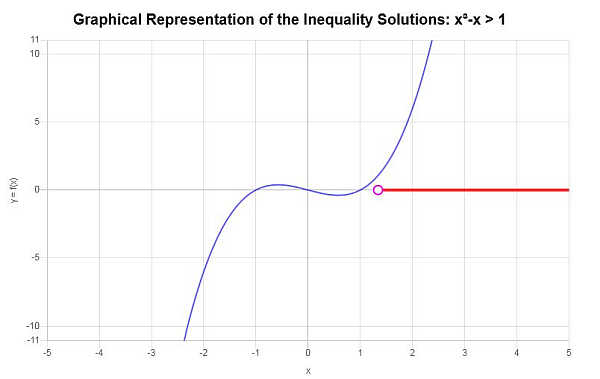
Sulla base della disuguaglianza fornita e analizzando i punti critici, troviamo che la soluzione della disuguaglianza è: \(x > 1.3247180451128\).

Utilizzando la notazione per intervalli, la soluzione si scrive come:

\[\left(1.3247180451128,\infty\right)\]

Graficamente:

Altre calcolatrici della disuguaglianza

Risolvere le disuguaglianze (vietato da trovare soluzioni alle equazioni ) è una delle operazioni più comuni in matematica, in generale.

Il processo di risoluzione delle disuguaglianze è solitamente laborioso e in generale non esiste una regola per risolverle. Risolvere disuguaglianze polinomiali è una delle poche eccezioni in cui possiamo seguire una serie di passaggi per trovare le soluzioni, ma possiamo comunque fallire, perché i polinomi di grado superiore sono difficili da trattare. In effetti, è davvero impossibile trovare le radici dei polinomi superiore al grado 5 utilizzando una regola generale (Teorema di Abel).