Ulteriori informazioni sulla composizione delle funzioni

Questo calcolatore te lo permetterà calcolare una funzione composto \(f \circ g\) basato su due funzioni \(f\) e \(g\) fornite. Si noti che in generale \(f \circ g\) non è lo stesso di \(g \circ f\) quindi l'ordine è rilevante.

Quando si calcola la composizione \(f \circ g\), c'è una funzione interna \(g\) e una funzione esterna \(f\), e si cambia l'ordine, molto spesso il risultato varia.

Osserva che \(f\) e \(g\) devono essere funzioni definite in modo valido, come ad esempio \(f(x) = \sqrt{x}\) e \(g(x) = 2x+1\), quindi avremmo quel \((f \circ g)(x) = f(g(x)) = \sqrt{2x+1}\) .

Cos'è una funzione composta?

Per formare una funzione composta, si valuta una funzione all'interno di un'altra funzione. Siano funzioni \(f\) e \(g\), la funzione composta è definita come

\[\displaystyle (f \circ g)(x) = f(g(x)) \]

Quali sono i passaggi per trovare la funzione composta?

• Passaggio 1: identifica le funzioni f e g per le quali eseguirai la composizione della funzione
• Passaggio 2: stabilire chiaramente la funzione interna ed esterna. In questo caso assumiamo che f sia la funzione esterna e g sia la formula interna
• Passaggio 3: la funzione composta è definita come (f◦g)(x) = f(g(x))

Puoi semplificare l'output risultante di f(g(x)) e, infatti, la calcolatrice lo semplificherà per te. Un punto importante è rendersi conto che potrebbe essere necessario restringere il dominio della funzione composita in modo che sia ben definito.

Cos'è un calcolatore di nebbia

In questo caso, fog non è la nebbia che conosci, si riferisce alla composizione di f e g, scritta come \(f \circ g\).

La composizione delle funzioni sarà tanto coinvolta algebricamente quanto la complessità delle funzioni che le compongono. Cioè, la composizione di semplici funzioni porterà a una semplice funzione composta, che è facile da calcolare.

Usando questo calcolatore composito

Il vantaggio dell'utilizzo di questo calcolatore composito è che otterrai la funzione composta calcolata e semplificata nei suoi termini più semplici, ma otterrai anche la funzione composta rappresentata graficamente.

Catena di funzioni composte

La composizione può essere applicata a più di due funzioni. Ad esempio, si considerino le funzioni \(f\), \(g\) e \(h\). La composizione della catena è definita come

\[\displaystyle (f \circ g \circ h)(x) = f(g(h(x))) \]

dove l'ordine in cui componi le espressioni è rilevante.

Dominio del calcolatore di funzioni composte

Si noti che il dominio di una funzione composta può essere diverso da quello delle due funzioni originali. Ad esempio, rivediamo il caso di \(f(x) = \sqrt{x}\) e \(g(x) = 2x+1\). Il dominio di f è \([0, \infty)\) e il dominio di g è \((-\infty, \infty)\), ma poiché \((f\circ g)(x) = \sqrt{2x+1}\), il dominio di \(f\circ g\) è \([-\frac{1}{2}, \infty)\).

Esempio: composizione di funzioni

Calcolare e rappresentare graficamente: \((f \circ g)(x)\) per \(f(x) = \sqrt{x}\) e \(g(x) = 2x-1\).

Soluzione: Sono state fornite le seguenti funzioni: \(\displaystyle f(x)=\sqrt{x}\) e \(\displaystyle g(x)=2x-1\), per le quali occorre calcolare la funzione composta \(f \circ g\).

Per definizione, la funzione composta \(f \circ g\) è definita come:

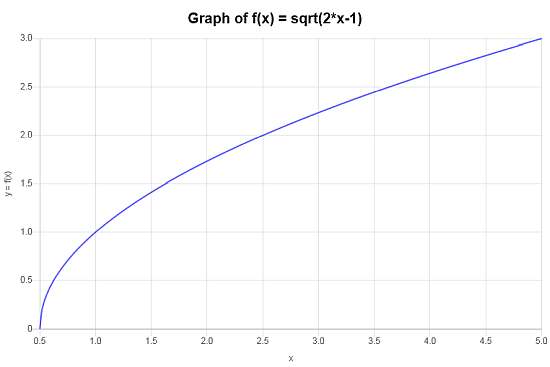
\[\begin{array}{ccl} f \circ g & = & f(g(x)) \\\\ & = & \sqrt{2x-1} \end{array}\]

Non c'è nulla da semplificare in questo caso, quindi la funzione composta che stiamo cercando è \(f \circ g(x)=\sqrt{2x-1}\).

Si ottiene il seguente grafico per la funzione composta \(f \circ g(x)=\sqrt{2x-1}\) sull'intervallo \([-5, 5]\):

Esempio: calcolo della funzione composta

Calcolare e rappresentare graficamente: \((f \circ g)(x)\) per \(f(x) = x^{3/2}\) e \(g(x) = x+2\). \((f \circ g)(x)\) è uguale a \((g \circ f)(x)\) in questo caso?

Soluzione: Queste sono le funzioni che dobbiamo comporre: \(\displaystyle f(x)=x^{3/2}\) e \(\displaystyle g(x)=x+2\).

Per definizione, la funzione composta \(f \circ g\) è definita come:

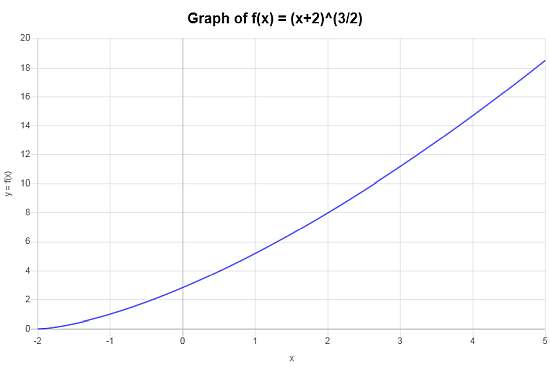
\[\begin{array}{ccl} f \circ g & = & f(g(x)) \\\\ & = & \left(x+2\right)^{3/2} \end{array}\]

Non c'è nulla da semplificare in questo caso, quindi la funzione composta che stiamo cercando è \(f \circ g(x)=\left(x+2\right)^{3/2}\).

Il seguente grafico è ottenuto per la funzione composta \(f \circ g(x)=\left(x+2\right)^{3/2}\) sull'intervallo \([-5, 5]\):

Esempio: esempio di calcolo della funzione composta

Trova \((f \circ g)(x)\) per \(f(x) = x^2\) e \(g(x) = x-2\) e rappresenta graficamente la funzione composta.

Soluzione: In questo esempio dobbiamo lavorare con \(\displaystyle f(x)=x^2\) e \(\displaystyle g(x)=x-2\), che ci richiede di calcolare la funzione composta. \(f \circ g\).

Usando la definizione, la funzione composta \(f \circ g\) è definita come:

\[\begin{array}{ccl} f \circ g & = & f(g(x)) \\\\ & = & \left(x-2\right)^2 \end{array}\]

L'espressione di cui sopra deve essere semplificata e i passaggi sono i seguenti:

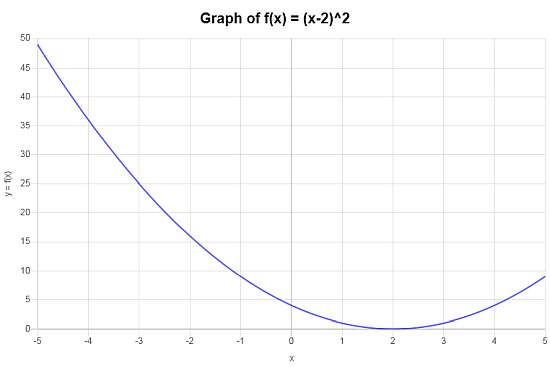
Allora, dopo aver semplificato, la funzione composta che si ottiene è \(f \circ g(x)=x^2-4x+4\).

La funzione composta \(f \circ g(x)=x^2-4x+4\) porta al seguente grafico sull'intervallo \([-5, 5]\):

Altri calcolatori di algebra

Funzioni sono uno degli elementi principali dell'algebra e del calcolo. E il motivo è che incarna un modo per stabilire una relazione tra due variabili x e y.

Molte applicazioni dipendono dalle operazioni che esegui e anche dal grafico di una funzione , che contiene tutte le informazioni "memorizzate" nella funzione.