Calcolatore di approssimazione lineare

Questo calcolatore di linearizzazione consentirà di calcolare l'approssimazione lineare, nota anche come Linea tangente per ogni data funzione valida, in un dato punto valido.

Devi fornire una funzione valida come ad esempio f(x) = x*sin(x), o f(x) = x^2 - 2x + 1, o qualsiasi funzione valida che sia differenziabile, e un punto \(x_0\) dove la funzione è ben definita. Questo punto può essere qualsiasi espressione numerica valida, ad esempio 1/3.

Dopo aver fornito una funzione e un punto validi, fai clic su "Calcola" e tutti i calcoli verranno visualizzati per te.

Approssimazione lineare o di primo ordine cerca un'approssimazione della funzione data da una linea, in un dato punto \(x_0\). Naturalmente per le curve un'approssimazione lineare sarà approssimativa, anche se l'idea principale è che l'approssimazione sarà accurata per punti vicini a \(x_0\).

Approssimazione lineare

L'idea è quella di trovare una retta che passi per il punto \((x_0, f(x_0))\) e che "tocchi appena" la funzione \(f(x)\). La definizione matematica formale di 'appena toccante' è data dall'idea di Linea tangente , per il quale abbiamo bisogno di Calcola la derivata della funzione.

Infatti la formula per l'approssimazione lineare nel punto \(x_0\) dipende dalla derivata \(f'(x_0)\), come segue

\[\displaystyle y = f(x_0) + f'(x_0) (x - x_0) \]

Questo formula di approssimazione lineare definisce essenzialmente il equazione di una retta che passa per il punto \((x_0, f(x_0))\), motivo per cui si chiama "approssimazione lineare", in quanto definisce una funzione lineare che coincide con \(f(x)\) nel punto \(x_0\), ed è molto vicina a \(f(x)\) per valori di \(x\) vicini a \(x_0\).

Passi per trovare l'approssimazione lineare

• Passo 1: Devi avere una data funzione f(x) e un punto x0. La funzione deve essere differenziabile in x0
• Passo 2: Calcolare f(x0) e f'(x0), che sono la funzione e la derivata della funzione f nel punto x0
• Passaggio 3: Definire l'approssimazione lineare come y = f(x_0) + f'(x_0) (x - x_0), che è la formula di linearizzazione presentata sopra

Questa linea, \(y = f(x_0) + f'(x_0) (x - x_0)\) rappresenta l'approssimazione di primo ordine, nota anche come approssimazione lineare locale.

Collegamento con linea tangente

Come probabilmente avrai già sospettato, l'approssimazione lineare è la stessa di Linea tangente al punto dato. Quindi, calcolare l'approssimazione lineare è esattamente come calcolare la linea tangente

Un altro nome per lo stesso è approssimazione del primo ordine, o approssimazione della linea tangente, che sono nomi comunemente usati anche in Calculus.

Approssimazione differenziale e lineare

Un altro concetto comune è quello di differenziale, che è strettamente legato a quello di approssimazione lineare, e ne è semplicemente una derivazione. Infatti, il differenziale (o differenza finita) è definito come \(\Delta y = y - f(x_0)\). Quindi, in base alla formula di approssimazione del primo ordine, la formula per il differenziale è:

\[\displaystyle \Delta y = y - f(x_0) = f'(x_0) (x - x_0) = f'(x_0) \Delta x \]

Questo naturalmente sembra esattamente come la formula di approssimazione lineare, tranne per il fatto che il termine \(f(x_0\) viene passato a sinistra.

Esempio: calcolo dell'approssimazione del primo ordine.

Considera quanto segue: \(f(x) = x^2 - 2x + 3\), trova la sua approssimazione di primo ordine in \(x_0 = 1\).

Soluzione: La funzione che è stata fornita è \(\displaystyle f(x)=x^2-2x+3\), e dobbiamo trovare l'approssimazione lineare attorno al punto x = 1. Quindi, prima abbiamo bisogno della derivata.

Approssimazione Lineare : L'equazione per l'approssimazione lineare che cerchiamo nel punto \(x_0 = 2\) è data dalla seguente formula

\[y = y_0 + f'(x_0)(x - x_0) \]

Si noti che per definizione \(\displaystyle y_0 = f(x_0)\), il che implica che dobbiamo collegare la funzione al punto \(x_0 = 2\) :

\[y_0 = f(x_0) = f\left(2\right) = 2^2-2\cdot 2+3 = 3\]

Facciamo lo stesso, ma ora per la derivata nel punto \(x_0 = 2\), allora

\[f'(x_0) = f'\left(2\right) = 2\cdot 2-2 = 2 \]

Ora con questo, torniamo alla formula di approssimazione lineare:

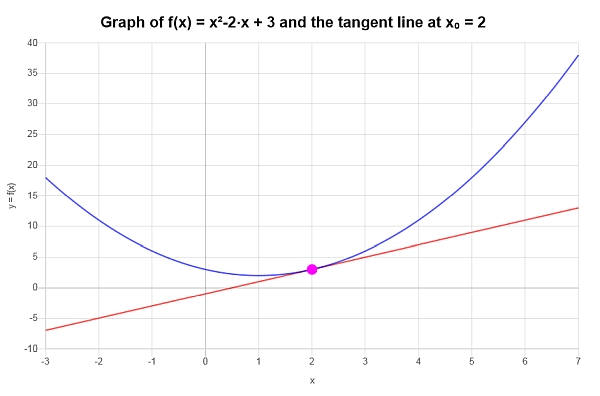
\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 3+2\left(x-2\right) = 2x-1 \]

Conclusione : Concludiamo che l'approssimazione lineare per \(\displaystyle f(x)=x^2-2x+3\) in \(x_0 = 2\) è data da:

\[y = 2x-1 \]

Graficamente:

Esempio: più approssimazione del primo ordine

Per la funzione : \(f(x) = x \sin(x)\) e il punto \(x_0 = 2\), trovare la corrispondente approssimazione del primo ordine.

Soluzione: In questo caso la funzione che dobbiamo lavorare è: \(\displaystyle f(x)=x\sin\left(x\right)\).

Calcoliamo ora la sua derivata:

Approssimazione Lineare : L'equazione dell'approssimazione lineare è:

\[y = y_0 + f'(x_0)(x - x_0) \]

dove \(\displaystyle y_0 = f(x_0)\), quindi calcoliamo:

\[y_0 = f(x_0) = f\left(2\right) = 2\sin\left(2\right)\]

Per la derivata in \(x_0 = 2\) troviamo che:

\[f'(x_0) = f'\left(2\right) = 2\cos\left(2\right)+\sin\left(2\right) \]

Ora siamo pronti per rimetterli nella formula di approssimazione del primo ordine:

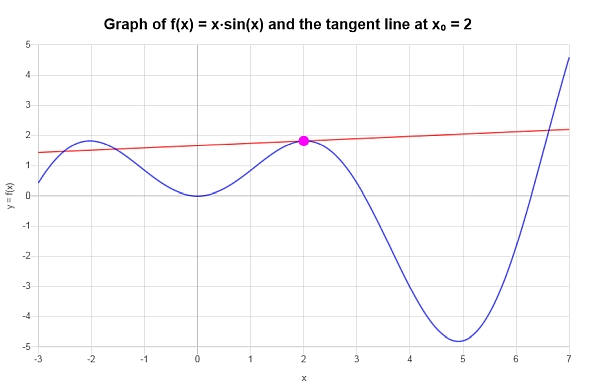
\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 2\sin\left(2\right)+2\cos\left(2\right)+\sin\left(2\right)\left(x-2\right) = 2x\cos\left(2\right)+x\sin\left(2\right)-4\cos\left(2\right) \]

Conclusione : Si conclude che l'approssimazione lineare di \(\displaystyle f(x)=x\sin\left(x\right)\) nel punto dato \(x_0 = 2\) è calcolata come:

\[y = 2x\cos\left(2\right)+x\sin\left(2\right)-4\cos\left(2\right) \]

Graficamente otteniamo il seguente grafico:

Esempio: calcolo dell'approssimazione lineare

Calcola l'approssimazione del primo ordine per \( f(x) = \frac{\sin(x)}{x}\) in \(x = \frac{\pi}{4}\).

Soluzione: E' stata fornita la seguente funzione: \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), per la quale dobbiamo calcolare la sua derivata.

La funzione è già stata semplificata, quindi possiamo procedere direttamente al calcolo della sua derivata:

Approssimazione Del Primo Ordine : L'equazione per l'approssimazione del primo ordine corrispondente per la data funzione \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\) nel punto dato \(x_0 = \frac{\pi}{4}\) è data da quanto segue:

\[y = y_0 + f'(x_0)(x - x_0) \]

Collegando i valori corrispondenti:

\[y_0 = f(x_0) = f\left(\frac{\pi}{4}\right) = \frac{\sin\left(\frac{\pi{}}{4}\right)}{\frac{\pi{}}{4}} = \frac{2\sqrt{2}}{\pi{}}\] \[f'(x_0) = f'\left(\frac{\pi}{4}\right) = \frac{\cos\left(\frac{\pi{}}{4}\right)}{\frac{\pi{}}{4}}-\frac{\sin\left(\frac{\pi{}}{4}\right)}{\left(\frac{\pi{}}{4}\right)^2} = \frac{2\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}}{\pi{}^2} \]

Quindi ora possiamo inserire questo nella formula:

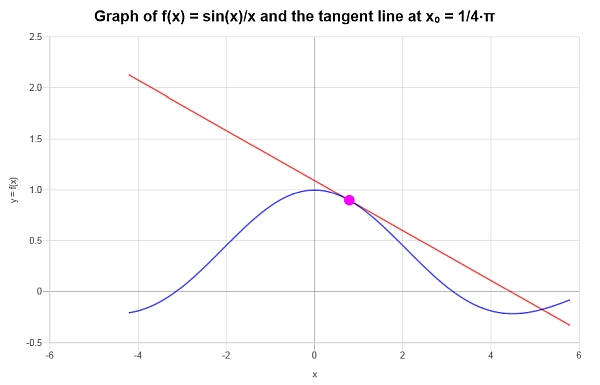
\[y = y_0 + f'(x_0)(x - x_0) \] \[\Rightarrow y = \frac{2\sqrt{2}}{\pi{}}+\frac{2\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}}{\pi{}^2}\left(x-\frac{1}{4}\pi{}\right) = -\frac{1}{2}\sqrt{2}+\frac{2\sqrt{2}x}{\pi{}}+\frac{4\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}x}{\pi{}^2} \]

Conclusione : Possiamo concludere quindi che l'approssimazione di primo ordine per la data funzione \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\) nel punto dato \(x_0 = \frac{\pi}{4}\) è data da

\[y = -\frac{1}{2}\sqrt{2}+\frac{2\sqrt{2}x}{\pi{}}+\frac{4\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}x}{\pi{}^2} \]

Graficamente si ottiene:

Altri calcolatori derivati

A parte questo calcolatore di linearizzazione , puoi trovare molte cose che fanno cose diverse basate su derivati. La differenziazione è un'operazione cruciale in Calcolo, Fisica, Ingegneria ed Economia, con un ampio spettro di applicazioni.

C'è anche un modo per eseguire un'approssimazione lineare per più variabili, ad esempio per una funzione \f(x, y)\), nel qual caso la formula dell'approssimazione lineare diventa \(f(x, y) = f(x_0, y_0) + \frac{\partial f}{\partial x}(x_0, y_0)(x-x_0) + \frac{\partial f}{\partial y}(x_0, y_0)(y-y_0)\), quindi in questo caso, per trovare la linearizzazione che dobbiamo usare derivate parziali .

Trovare la linearizzazione di una funzione non è di gran lunga l'unica cosa che puoi fare con le derivate. La differenziazione è un'operazione relativamente facile con regole semplici come il Regola Del Prodotto , la regola del quoziente e il Regola Di Derivazione ciò rende il calcolo delle derivate un'operazione relativamente semplice.

Anche se dovrebbe essere semplice, è una buona idea usare a calcolatore derivato per ottenere tutti i passaggi mostrati, con una chiara menzione di tutti i Regole derivate usato.