La regola del quoziente

Questa calcolatrice ti consentirà di utilizzare la regola del quoziente per una funzione che coinvolge un quoziente, mostrando tutti i passaggi del processo. Tutto quello che devi fornire è una funzione differenziabile valida. Questa funzione deve coinvolgere almeno un quoziente affinché la regola del quoziente sia applicabile.

Un esempio di una funzione valida sarebbe f(x) = (x^2 + 2x + 1)/(x^2-1), o qualcosa come f(x) = sin(x)/x, ecc.

Una volta fornita una funzione valida che coinvolge i quozienti, è necessario fare clic sul pulsante "Calcola" per visualizzare i passaggi del calcolo.

Insieme con il Regola Del Prodotto e Regola Di Derivazione , il Regola Del Quoziente è una delle basi più importanti Regole derivate .

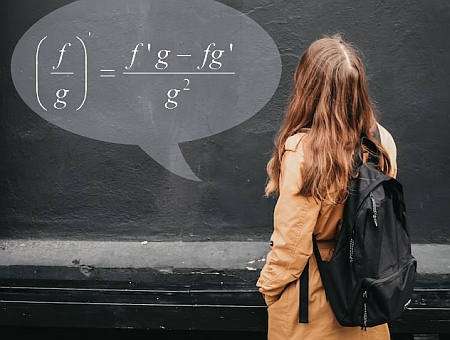
Formula della regola del quoziente

In termini semplici, il Regola Del Quoziente ti aiuta a calcolare la derivata di un quoziente, sfruttando la conoscenza delle singole funzioni e delle loro derivate. La formula della regola del quoziente è:

\[\displaystyle \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) = \displaystyle \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} \]

Quali sono i passaggi per utilizzare la regola del quoziente?

• Fase 1: Identifica chiaramente le funzioni f(x) e g(x) che vanno al numeratore e al denominatore del quoziente
• Passo 2: Semplifica qualsiasi termine ovvio che può essere semplificato
• Smusso 3: Calcolare le derivate corrispondenti f'(x) e g'(x)
• Passaggio 4: Inserire i valori trovati nel passaggio 3 nella formula \(\displaystyle \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) = \displaystyle \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} \)

Si noti che f(x) e g(x) possono ancora essere funzioni complesse, quindi potrebbe essere necessario utilizzare altre regole come la regola della catena per calcolare sia f'(x) che g'(x).

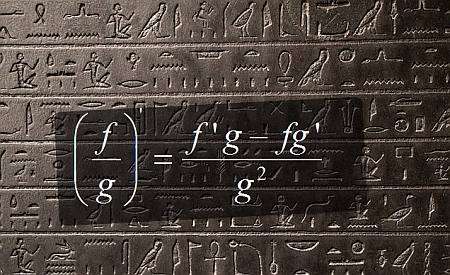
Derivata della regola dei quozienti

Quando si calcola una derivata della regola del quoziente, si riduce la derivata di un quoziente alla conoscenza delle derivate individuali, ma tali derivate individuali possono comunque richiedere molti passaggi con Regole di derivata di base da risolvere.

Questo è il motivo per cui la differenziazione è considerata un'operazione "semplice", tuttavia, è necessario organizzare sufficientemente e tenere traccia di tutti i pezzi che si presentano durante la scomposizione con regole derivate, quindi procedere con i pezzi più piccoli che potrebbero richiedere più regole di differenziazione per essere applicato.

Quindi potresti finire con un processo iterativo, ma è garantito che a un certo punto finirà andando più a fondo in ogni parte più piccola, finché non trovi una derivata elementare, come un polinomio o un derivata trigonometrica .

Regola dei quozienti nella differenziazione

Il ruolo del regola dei quozienti nella differenziazione è piuttosto importante, una buona ragione per cui vorrai usare una calcolatrice per questo. In termini algebrici, la regola del quoziente potrebbe essere considerata più contorta della regola del prodotto, e potrebbe essere vera in molti casi, ma alla fine dipende dalla complessità delle funzioni al numeratore e al denominatore.

Esempi di regole del quoziente

Considera la funzione: \(f(x) = \frac{x^2+1}{x-2}\), trova la sua derivata.

Soluzione: Per questo esempio, dobbiamo analizzare la funzione \(\displaystyle f(x)=\frac{x^2+1}{x-2}\), in termini di ricerca della sua derivata.

Conclusione : Troviamo che la derivata della funzione data è:

\[f'(x) = \frac{x^2-4x-1}{\left(x-2\right)^2}\]

Quindi, la rappresentazione grafica della funzione e della sua derivata è \([-5, 5]\):

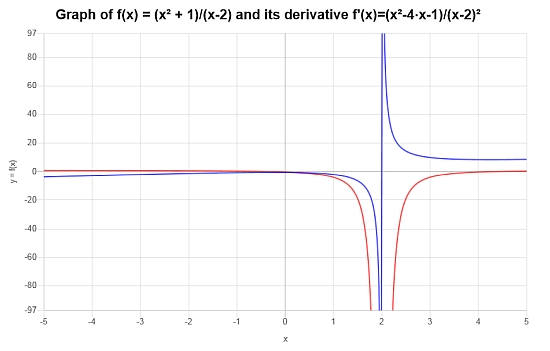
Esempio: calcolo della regola del quoziente

Ora considera \(f(x) = \frac{x}{\sin(x)}\), trova la sua derivata usando la regola del quoziente.

Soluzione: Per questo secondo esempio, la funzione che ci interessa è \(\displaystyle f(x)=\frac{x}{\sin\left(x\right)}\). Distinguiamolo usando la regola del quoziente.

Conclusione : La conclusione è che, in base al calcolo precedente, la derivata è data da:

\[f'(x) = \frac{-\left(x\cos\left(x\right)-\sin\left(x\right)\right)}{\sin\left(x\right)^2}\]

Graficamente, possiamo vedere la funzione (in blu) e la sua derivata (in rosso):

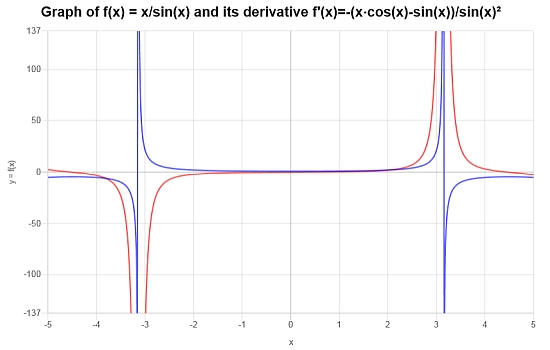
Altri esempi di regole del quoziente

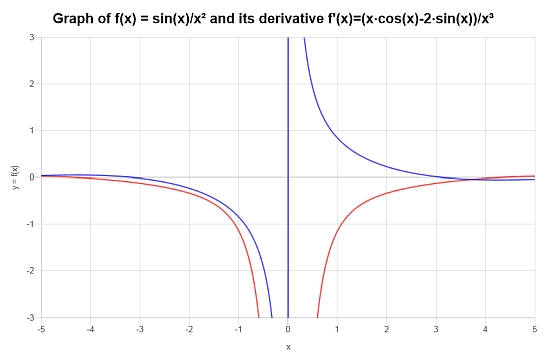
Infine, considera la funzione: \(f(x) = \frac{\sin(x)}{x^2}\), trova la sua derivata.

Soluzione: Per questo esempio di regola del quoziente finale lavoriamo con la funzione \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x^2}\). .

Conclusione : Per la funzione data, la sua derivata è:

\[f'(x) = \frac{x\cos\left(x\right)-2\sin\left(x\right)}{x^3}\]

Il grafico seguente mostra la situazione per \(f\) e \(f'\):

Più calcolatori derivati

In Calculus lo farai trovare derivati ovunque guardi. Ci sono migliaia di applicazioni che li coinvolgono rendendoli sui più importanti strumenti per la Scienza e l'Ingegneria.

Avrete bisogno di conoscere Differenziazione implicita per applicazioni diverse che spesso comportano tariffe correlate o nel calcolo multivariato che ti interesserà trovare le derivate parziali .

Nel complesso, troverai la tua vita più facile quando hai a che fare con i derivati se sei in grado di gestire correttamente i più comuni Regole derivate , includendo il Regola Di Derivazione , così come il Regola Del Prodotto e Regola Del Quoziente .