Risolutori Calcolo

Regole derivate

Istruzioni: Usa questo calcolatore derivato per trovare la derivata di qualsiasi funzione che fornisci, utilizzando le regole derivate più comuni, mostrando tutti i passaggi. Si prega di digitare la funzione a cui si desidera applicare le regole derivate nella casella del modulo sottostante.

Informazioni sulle regole derivate

Questo calcolatore ti consentirà di calcolare la derivata di una funzione che fornisci applicando le regole di differenziazione di base richieste, mostrando tutti i passaggi del processo e notando dove viene applicata ciascuna regola.

Devi solo fornire una funzione valida che sia differenziabile (il che significa che ha una derivata). Ad esempio, una funzione valida potrebbe essere f(x) = 1/3*x*sin(x), solo per citare un esempio.

Quindi, quando hai già digitato la tua funzione, fai clic su "Calcola" per ottenere tutti i passaggi della differenziazione mostrata.

La semplicità delle regole delle derivate rende il processo di differenziazione riconosciuto come 'facile', un giudizio che forse è un'esagerazione.

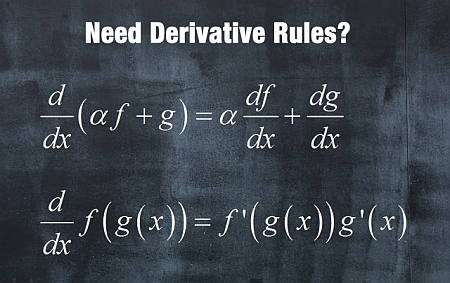
Regole di derivata di base

Ci sono quattro regole derivate di base da imparare

Regola Di Linearità: Per le funzioni \(f(x)\) e \(g(x)\) e una costante \(a\), la derivata è un'operazione lineare: \((af(x)+g(x))' = af'(x)+g'(x)\)
Regola Del Prodotto Per le funzioni \(f(x)\) e \(g(x)\), la derivata del prodotto è \((f(x)g(x))' = f'(x)g(x) + f(x)g'(x)\)
Regola Del Quoziente: Per le funzioni \(f(x)\) e \(g(x)\), la derivata del quoziente è \(\left(\frac{f(x)}{g(x)}\right)' = \left(\frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)}\right)\)
Regola Di Derivazione Per le funzioni \(f(x)\) e \(g(x)\), la derivata della funzione composta è \((f(g(x)))' = f'(g(x))g'(x)\)

Queste regole funzioneranno come un incantesimo e ti aiuteranno a trovare la derivata di qualsiasi funzione di base.

Come usare le regole derivate?

Fase 1: Identifica la funzione f(x) che vuoi differenziare, semplifica se necessario
Passo 2: Prova a suddividere la funzione in blocchi derivativi più piccoli, usando la linearità
Smusso 3: A seconda della struttura della funzione f(x), utilizzare una qualsiasi delle regole disponibili (regola del prodotto, del quoziente e della catena) e tenere presente che potrebbe essere necessario applicare molte delle regole consecutivamente)

Di solito ti ritroverai con una combinazione di diverse regole di differenziazione, fino a raggiungere il punto in cui trovi una funzione elementare, di cui sai già come differenziare.

Posso risolvere tutte le derivate

Dire che l'uso delle regole di differenziazione può portarti a risolvere TUTTE le derivate può essere un'esagerazione. Sarai in grado di risolvere la MAGGIOR PARTE delle derivate, e sicuramente tutte quelle di base, ma ci sono funzioni che hanno un comportamento meno intuitivo che potrebbero essere definite, sebbene non siano tipicamente trattate nei corsi di Calcolo di base.

Per quanto riguarda le funzioni di base, la maggior parte di esse sarà differenziata senza problemi.

Un derivata della regola del prodotto , derivata della regola dei quozienti o derivata della regola della catena è improbabile che siano isolati e probabilmente arriveranno in una sequenza di diverse regole che devono essere utilizzate insieme.

Esempio: regole derivate

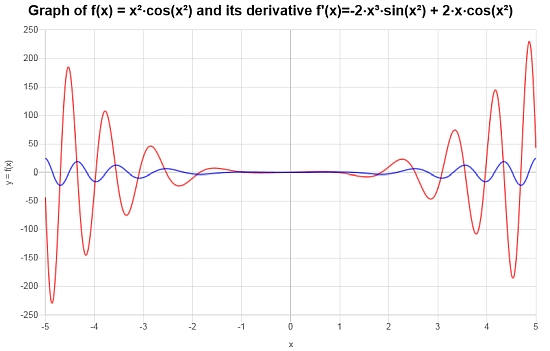
Usando le regole di derivata di base, calcola la seguente derivata: \(\frac{d}{dx}\left( x^2 \cos(x^2) \right)\)

Soluzione: Consideriamo la seguente funzione data per la quale occorre calcolare la derivata \(\displaystyle f(x)=x^2\cos\left(x^2\right)\)

La funzione non necessita di semplificazione, quindi possiamo procedere direttamente al calcolo della sua derivata:

\( \displaystyle \frac{d}{dx}\left(x^2\cos\left(x^2\right)\right)\)

Now, using the Product Rule: \(\frac{d}{dx}\left( x^2\cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right) \cdot \cos\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\cos\left(x^2\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right) \cdot \cos\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\cos\left(x^2\right)\right)\)

We have to use the Chain Rule: \(\frac{d}{dx}\left( \cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right)\cdot \left(-\sin\left(x^2\right)\right)\) and using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(2x\right) \cos\left(x^2\right)+x^2 \cdot 2x\cdot \left(-\sin\left(x^2\right)\right)\)

so then we get

\( \displaystyle = \,\,\)

\(\displaystyle x^2\cdot 2x\cdot \left(-\sin\left(x^2\right)\right)+2x\cos\left(x^2\right)\)

By reordering some of the numerical values, and then grouping the terms with \(x\) in the term \(x^2\cdot 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x^3\cdot \left(-\sin\left(x^2\right)\right)+2x\cos\left(x^2\right)\)

But we get \((2x^3) \cdot (-\sin\left(x^2\right)) = -2x^3\sin\left(x^2\right) = -2x^3\sin\left(x^2\right)\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle -2x^3\sin\left(x^2\right)+2x\cos\left(x^2\right)\)

And finally, grouping the terms together

\( \displaystyle = \,\,\)

\(\displaystyle -2\left(x^2\sin\left(x^2\right)-\cos\left(x^2\right)\right)x\)

Di seguito è riportato il grafico corrispondente della funzione e della sua derivata:

Esempio: regole più derivate

Calcola la seguente derivata: \(\frac{d}{dx}\left( x \cos(x^2+1) \right)\) utilizzando le regole di derivata di base.

Soluzione: Ora, il compito a portata di mano è quello di differenziare la funzione \(\displaystyle f(x)=x\cos\left(x^2+1\right)\)

\( \displaystyle \frac{d}{dx}\left(x\cos\left(x^2+1\right)\right)\)

In this case, we have to use the Product Rule: \(\frac{d}{dx}\left( x\cos\left(x^2+1\right) \right) = \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(\cos\left(x^2+1\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(\cos\left(x^2+1\right)\right)\)

The Chain Rule for this composition: \(\frac{d}{dx}\left( \cos\left(x^2+1\right) \right) = \frac{d}{dx}\left(x^2+1\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(x^2+1\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^2+1 \right) = \frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

The derivative of a constant is 0, so then:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(\frac{d}{dx}\left(x^2\right)\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

Using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(2x\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

which then leads to

\( \displaystyle = \,\,\)

\(\displaystyle x\cdot 2x\cdot \left(-\sin\left(x^2+1\right)\right)+\cos\left(x^2+1\right)\)

Putting together the numerical values and grouping the terms with \(x\) in the term \(x\cdot 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x^2\cdot \left(-\sin\left(x^2+1\right)\right)+\cos\left(x^2+1\right)\)

Observe that \((2x^2) \cdot (-\sin\left(x^2+1\right)) = -2x^2\sin\left(x^2+1\right) = -2x^2\sin\left(x^2+1\right)\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle -2x^2\sin\left(x^2+1\right)+\cos\left(x^2+1\right)\)

So then we get

\( \displaystyle = \,\,\)

\(\displaystyle -2x^2\cos\left(x^2\right)\sin\left(1\right)-2x^2\cos\left(1\right)\sin\left(x^2\right)+\cos\left(1\right)\cdot \cos\left(x^2\right)-\sin\left(1\right)\cdot \sin\left(x^2\right)\)

Esempio di regole derivate

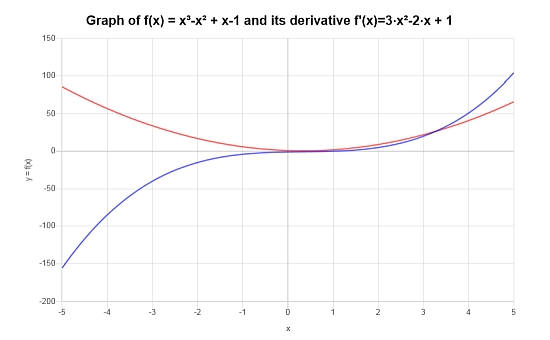
Per la funzione \( f(x) = (x-1)(x^2+1) \), utilizzare le regole di derivata per trovare la sua derivata.

Soluzione: Per questo esempio finale, dobbiamo differenziare: \(\displaystyle f(x)=\left(x-1\right)\left(x^2+1\right)\).

Passaggio Iniziale: In questo caso, dobbiamo prima espandere la funzione data \(\displaystyle f(x)=\left(x-1\right)\left(x^2+1\right) \) e, per farlo, eseguiamo i seguenti passaggi di semplificazione:

\( \displaystyle f(x)=\left(x-1\right)\left(x^2+1\right)\)

Note that \((x-1) \cdot (x^2+1) = x\cdot x^2+x-x^2-1^2 = x^3-x^2+x-1\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle x^3-x^2+x-1\)

Dopo aver espanso la funzione, possiamo procedere al calcolo della derivata:

\( \displaystyle \frac{d}{dx}\left(x^3-x^2+x-1\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^3-x^2+x-1 \right) = \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\)

The derivative of a constant is 0, so then:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)\)

We know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+1\)

Using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\) and \(\frac{d}{dx}\left( x^3 \right) = 3x^2\)

\( \displaystyle = \,\,\)

\(\displaystyle 3x^2-2x+1\)

Graficamente, ecco come appaiono la funzione e la sua derivata:

Più calcolatori derivati

Una delle magie della differenziazione è che puoi trova la derivata di qualsiasi funzione utilizzando alcune regole basilari e semplici, tra cui il Regola Del Prodotto , Regola Del Quoziente e naturalmente, la regola della catena . Questo piccolo arsenale di solito è sufficiente per calcolare qualsiasi derivato di cui hai bisogno

La differenziazione e l'integrazione sono le corsie principali in Calculus, senza alcuna discussione, poiché sono il centro di così tante applicazioni, in tutti gli aspetti della scienza. Dalle tariffe correlate a Differenziazione implicita , con derivate parziali in Fisica ed Economia