Ulteriori informazioni su questo calcolatore di vertici

Questa calcolatrice ti consentirà di ottenere una funzione quadratica che fornisci Forma del vertice , mostrando tutti i passaggi. Devi fornire un'espressione quadratica valida in x. Qualsiasi funzione quadratica valida funzionerà.

Ad esempio, puoi fornire qualcosa come x^2 + 3x + 4, oppure potresti fornire un'espressione non semplificata, come x^2 + 3x - 1/2 x + 3x^2 - 3.

Una volta fornita una funzione quadratica valida, ti basterà cliccare su "Calcola" e ti verrà mostrato il calcolo della forma del vertice, con tutti i passaggi previsti da questo Calcolatore parabola .

Ogni funzione quadratica validamente definita avrà una forma di vertice, da cui sarà diretto ottenere le coordinate del vertice, e se la parabola si apre "verso l'alto" o "verso il basso".

Come trovare la forma del vertice per una parabola?

Tutte le funzioni quadratiche sono rappresentate graficamente graficamente da una parabola. Questa parabola si aprirà verso l'alto o verso il basso, a seconda del segno del coefficiente principale.

In definitiva, ottenere la parabola in forma di vertice consiste nel trovare il vertice della funzione quadratica, che si ottiene con Completare la Piazza .

Quali sono i passaggi per calcolare la forma del vertice?

Così, come si trova la forma del vertice ? Puoi seguire questi passaggi:

• Passaggio 1: identificare la funzione quadratica. L'espressione deve avere grado 2 e il coefficiente principale che moltiplica x² deve essere diverso da zero
• Passaggio 2: se il coefficiente principale che moltiplica x² è positivo, la parabola si apre verso l'alto e se è negativo, si apre verso il basso
• Passaggio 3: completa i quadrati e nota il termine all'interno delle parentesi con x, perché determina la coordinata x del vertice
• Passaggio 4: dopo aver completato i quadrati, la costante all'esterno della parentesi (potrebbe essere zero) corrisponde alla coordinata y del vertice

Pertanto, possiamo vedere che il processo generale di calcolo della forma dei vertici è strettamente correlato al processo di completamento dei quadrati.

Esiste una formula dei vertici?

In effetti, sì, c'è. Normalmente, il completamento del processo dei quadrati è la lunga strada da percorrere. Supponiamo di avere un funzione quadratica , espresso da:

\[ f(x) = a x^2 + b x + c\]

Quindi, hai già una funzione quadratica semplificata. La coordinata x del vertice viene calcolata utilizzando la seguente formula:

\[ x_v = \displaystyle \frac{-b}{2a} \]

Davvero semplice, vero? SÌ. Ma allora, come si ottiene la coordinata y del vertice? Prendi il valore \(x_v\) e lo inserisci nella funzione quadratica. Quindi otteniamo

\[ y_v = f(x_v) = a x_v^2 + b x_v + c \]

Naturalmente, questa formula può essere molto più veloce che eseguire un processo di completamento dei quadrati, ma ogni metodo ha i suoi usi e le circostanze di un dato problema ti diranno che forma da usare. .

Forma quadratica a vertice?

Perché vorresti passare dalla forma quadratica a quella dei vertici? I motivi sono molteplici: da un punto di vista geometrico, la forma del vertice permette di vedere la data funzione quadratica come una traslazione e riscalatura di una parabola elementare, dove la traslazione è determinata dal vertice, e la scala è determinata con l'anteriore coefficiente.

Il calcolo può essere laborioso, ma questo Calcolatore parabola farà il lavoro sporco per te.

Forma da standard a vertice?

Di solito c'è un po' di confusione su questo. Permettetemi di chiarire, la forma del vertice è un altro nome dato alla forma standard. Allora, la forma standard di una funzione quadratica \(y = a(x-h)^2 + k\) è la stessa della forma del vertice.

La confusione deriva dal fatto che a volte le persone usano la forma generale di una quadratica quando si riferiscono alla forma standard. La forma generale è \(y = ax^2 + bx + c\).

Quindi, la domanda che ha senso è come passare dalla forma generale alla forma dei vertici, che equivale a chiedere come passare dalla forma generale alla forma standard. La risposta è semplice: inizia dalla forma generale e poi tu Completa i quadrati per arrivare alla forma standard.

Esempio: come trovare la forma del vertice

Trova il vertice della seguente espressione quadratica \(f(x) = x^2 + 3x - 6\) utilizzando la formula del vertice

Soluzione: Dobbiamo trovare la forma del vertice per la funzione quadratica \(\displaystyle f(x)=x^2+3x-6\).

Per prima cosa calcoliamo le coordinate del vertice per la parabola associata alla data funzione quadratica.

Per una funzione quadratica della forma \(f(x) = a x^2 + bx + c\), la coordinata x del vertice viene calcolata utilizzando la seguente formula:

\[x_V = \displaystyle -\frac{b}{2a}\]

In questo caso, abbiamo che la funzione di cui dobbiamo trovare il vertice per è \(f(x) = \displaystyle x^2+3x-6\), il che implica che i coefficienti corrispondenti sono:

\[a = 1\] \[b = 3\] \[c = -6\]

Inserendo i valori noti di \(a\) e \(b\) nella formula per la coordinata x del vertice, otteniamo:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot 1} = -\frac{3}{2}\]

Ora, dobbiamo inserire il valore di \(x_V = \displaystyle -\frac{3}{2}\) nella funzione quadratica, quindi otteniamo:

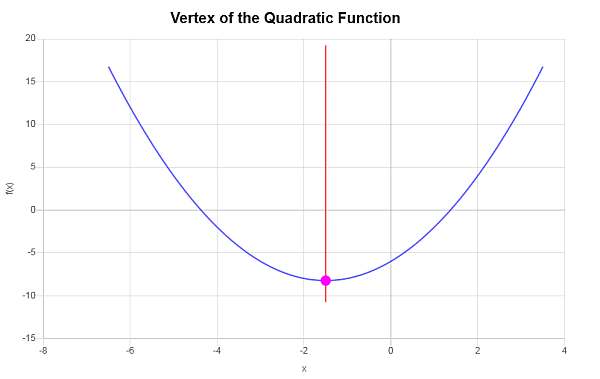
\[y_V = f(x_V)\] \[ = 1\cdot \left(-\frac{3}{2}\right)^2+3\cdot \left(-\frac{3}{2}\right)-6=1\cdot\frac{9}{4}+3\cdot \left(-\frac{3}{2}\right)-6=\frac{9}{4}+3\cdot \left(-\frac{3}{2}\right)-6=\frac{9}{4}-\frac{9}{2}-6=-\frac{33}{4}\]

Pertanto, la coordinata x del vertice è \(x_V = \displaystyle -\frac{3}{2}\) e la coordinata y del vertice è \(y_V = \displaystyle -\frac{33}{4}\). Questo indica che il punto che rappresenta il vertice è \( \displaystyle \left(-\frac{3}{2}, -\frac{33}{4}\right)\).

Graficamente si ottiene:

Dobbiamo completare il quadrato per l'espressione quadratica \(\displaystyle x^2+6x-2\).

Per completare il quadrato è necessario eseguire i seguenti passaggi:

Passo 1: In questo caso poiché la costante principale, il termine che moltiplica \(x^2\) nel dato polinomio, è \(a = 1\), quindi non lo scomponiamo.

Passo 2: Forziamo un '2' davanti al termine \(x\) osservando quel termine di ordine 1 nell'espressione quadratica data possiamo riscrivere: \(\displaystyle 6 x = 2 \cdot \left(3\right) x\), quindi otteniamo \[ x^2+6x-2 = x^2+2 \cdot \left(3\right) x-2 \]

Passaggio 3: Il termine che moltiplica 2 in questo caso è \(\displaystyle 3\), quindi per usare l'equazione binomiale, abbiamo bisogno che il suo quadrato \(\displaystyle \left(3\right)^2\) sia nell'espressione.

Per ottenere ciò, ora aggiungiamo e sottraiamo il termine \(\displaystyle \left(3\right)^2 = 9\), in modo da completare il quadrato. Aggiungere e sottrarre lo stesso termine equivale ad aggiungere zero, quindi non influisce sull'espressione: \[ \begin{array}{ccl} \displaystyle x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \end{array}\]

Passaggio 4: Completiamo il quadrato e semplifichiamo le costanti: \[ \begin{array}{ccl} x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x+9-2-9 \\\\ \\\\ & = & \displaystyle \left[x^2+2 \cdot \left(3\right) x+\left(3\right)^2\right]-2-9 \\\\ \\\\ & = & \displaystyle \left( x+3 \right)^2-11 \end{array}\]

Conclusione: Pertanto, troviamo che la funzione in forma di vertice è \(\displaystyle f(x) = \left( x+3 \right)^2-11\), che completa il calcolo.

Esempio: forma da quadratica a vertice

Converti la seguente forma quadratica \(f(x) = x^2 + 6x - 2\) in forma di vertice. Quali sono le coordinate del vertice? La parabola si apre verso l'alto o verso il basso?

Soluzione:

Dobbiamo trovare la forma del vertice per la funzione quadratica \(\displaystyle f(x)=x^2+6x-2\).

Per prima cosa calcoliamo le coordinate del vertice per la parabola associata alla data funzione quadratica.

Per una funzione quadratica della forma \(f(x) = a x^2 + bx + c\), la coordinata x del vertice viene calcolata utilizzando la seguente formula:

\[x_V = \displaystyle -\frac{b}{2a}\]

In questo caso, abbiamo che la funzione di cui dobbiamo trovare il vertice per è \(f(x) = \displaystyle x^2+6x-2\), il che implica che i coefficienti corrispondenti sono:

\[a = 1\] \[b = 6\] \[c = -2\]

Inserendo i valori noti di \(a\) e \(b\) nella formula per la coordinata x del vertice, otteniamo:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{6}{2 \cdot 1} = -3\]

Ora, dobbiamo inserire il valore di \(x_V = \displaystyle -3\) nella funzione quadratica, quindi otteniamo:

\[y_V = f(x_V)\] \[ = 1\cdot \left(-3\right)^2+6\cdot \left(-3\right)-2=1\cdot \left(-3\right)^2+6\cdot \left(-3\right)-2=-3^2+6\cdot \left(-3\right)-2=9-18-2=-11\]

Pertanto, la coordinata x del vertice è \(x_V = \displaystyle -3\) e la coordinata y del vertice è \(y_V = \displaystyle -11\). Questo indica che il punto che rappresenta il vertice è \( \displaystyle \left(-3, -11\right)\).

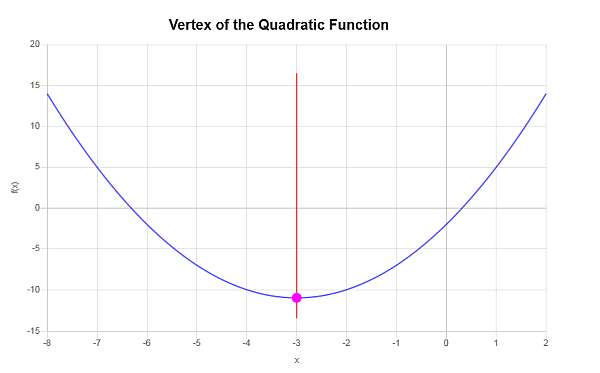
Dobbiamo completare il quadrato per l'espressione quadratica \(\displaystyle x^2+6x-2\).

Per completare il quadrato è necessario eseguire i seguenti passaggi:

Passo 1: In questo caso poiché la costante principale, il termine che moltiplica \(x^2\) nel dato polinomio, è \(a = 1\), quindi non lo scomponiamo.

Passo 2: Forziamo un '2' davanti al termine \(x\) osservando quel termine di ordine 1 nell'espressione quadratica data possiamo riscrivere: \(\displaystyle 6 x = 2 \cdot \left(3\right) x\), quindi otteniamo \[ x^2+6x-2 = x^2+2 \cdot \left(3\right) x-2 \]

Passaggio 3: Il termine che moltiplica 2 in questo caso è \(\displaystyle 3\), quindi per usare l'equazione binomiale, abbiamo bisogno che il suo quadrato \(\displaystyle \left(3\right)^2\) sia nell'espressione.

Per ottenere ciò, ora aggiungiamo e sottraiamo il termine \(\displaystyle \left(3\right)^2 = 9\), in modo da completare il quadrato. Aggiungere e sottrarre lo stesso termine equivale ad aggiungere zero, quindi non influisce sull'espressione: \[ \begin{array}{ccl} \displaystyle x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \end{array}\]

Passaggio 4: Completiamo il quadrato e semplifichiamo le costanti: \[ \begin{array}{ccl} x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x+9-2-9 \\\\ \\\\ & = & \displaystyle \left[x^2+2 \cdot \left(3\right) x+\left(3\right)^2\right]-2-9 \\\\ \\\\ & = & \displaystyle \left( x+3 \right)^2-11 \end{array}\]

Conclusione: Pertanto, troviamo che la funzione in forma di vertice è \(\displaystyle f(x) = \left( x+3 \right)^2-11\), che completa il calcolo.

Altri calcolatori quadratici

La maggior parte calcolatrici quadratiche fare affidamento in un modo o nell'altro sul processo di completando i quadrati , che consente di raggruppare elementi all'interno di parentesi quadrate.

Come possiamo vedere nella formula del vertice, il calcolo del vertice è strettamente legato al formula quadratica e il radici di calcolo dell'equazione quadratica . .