Informazioni sulla regola della catena

Questo calcolatore ti consentirà di applicare la regola della catena a qualsiasi funzione composita che fornisci. UN Funzione composta corrisponde al caso in cui si valuta una funzione all'interno di una funzione. Affinché il calcolatore della regola della catena funzioni, è necessario fornire una funzione composita valida e differenziabile.

Un esempio di una funzione valida sarebbe f(x) = (sin(x))^2, dove qui abbiamo la funzione 'x^2' che viene valutata in un'altra funzione, che è sin(x), formando un funzione composita.

Una volta fornita una funzione valida e differenziabile, la prossima cosa che devi fare è cliccare sul pulsante che dice "Calcola", che poi metterà in moto i calcoli e ti verranno mostrati tutti i passaggi.

La derivata della regola della catena è una delle regole di differenziazione più comunemente utilizzate. Questo perché la composizione della funzione è uno dei modi più naturali per costruire nuove funzioni basate su quelle elementari.

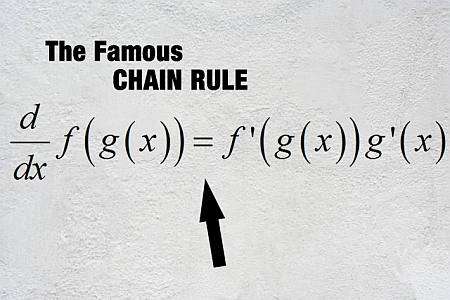
Qual è la regola della catena

In parole semplici, la Chain Rule permette di differenziare funzioni composite, cioè funzioni che vengono valutate all'interno di altre funzioni. Quindi, supponiamo di avere la funzione \(f(x)\) e \(g(x)\), e di sapere come calcolare la derivata di queste funzioni, che sono \(f'(x)\) e \(g'(x)\).

Poi c'è un Formula della regola della catena che ci permette di calcolare la derivata della funzione composta \(f \circ g\), che è definita come \((f \circ g)(x) = f(g(x))\):

\[\displaystyle (f \circ g)'(x) = f'(g(x))g'(x)\]

Passaggi per l'utilizzo della regola della catena

• Fase 1: Identificare la funzione esterna f(x) e la funzione interna g(x)
• Passo 2: Assicurati che f(x) e g(x) siano funzioni valide e differenziabili e calcola le derivate corrispondenti f'(x) e g'(x)
• Smusso 3: Usa la formula (f \circ g)'(x) = f'(g(x))g'(x), che indica che valutiamo la derivata della funzione esterna alla funzione interna, e moltiplichiamola per la derivata della funzione interna

Osserva come i passaggi precedenti utilizzano l'idea di funzione "interna" ed "esterna". Forse non è un termine standard, ma piuttosto un'idea che può aiutarti a identificare il ruolo svolto da ciascuna funzione quando usi la regola della catena.

Applicazioni della regola della catena

La regola della catena è davvero uno strumento eccellente per trovare i derivati e normalmente sarà la chiave di qualsiasi calcolatore di derivate , insieme a tutti gli altri basic Regole derivate . Ma la regola della catena ha un'interpretazione speciale in quella che viene chiamata Tariffe Correlate

Per dare un contesto all'idea di tariffe correlate, iniziamo con una forma di scrittura della regola della catena che forse molte persone troveranno più facile da comprendere:

\[\displaystyle \frac{dy}{dx} = \displaystyle \frac{dy}{dz} \cdot \frac{dz}{dx} \]

La forma precedente della regola della catena dice che se \(y\) è una funzione di \(z\) e \(z\) è una funzione di \(x\), allora alla fine \(y\) è una funzione di \(x\), e puoi trovare la derivata di \(y\) rispetto a \(x\) usando la regola della catena.

Come probabilmente avrai sospettato, \(y\) svolge il ruolo di \(f(x)\) (la funzione 'esterna') e \(z\) svolge il ruolo di \(g(x)\) (la funzione 'interna').

La suddetta forma della regola della catena collega il tasso di variazione di y rispetto a x, con i tassi di variazione di y rispetto a ze quello di z rispetto a x, e quindi il termine "tassi correlati".

Questo è estremamente utile nella pratica. Esempio: il raggio di un cerchio sta aumentando a una velocità di 2 cm/sec, qual è la velocità di variazione dell'area del cerchio? Quindi, puoi esprimere il raggio del cerchio in funzione di t, riflettendo il fatto che aumenta a una velocità di 2 cm/sec, OPPURE puoi usare la regola della catena.

Quindi chiami A l'area, r il raggio e t il tempo. Quello che devi calcolare è \(\displaystyle \frac{dA}{dt}\), quindi usi direttamente la regola della catena, poiché conosci \(A = \pi r^2\) e r'(t) = 2, quindi allora

\[\displaystyle \frac{dA}{dt} = \displaystyle \frac{dA}{dr} \cdot \frac{dr}{dt} = 2\pi r \cdot 2 = 4 \pi r \]

Regola della catena di derivata parziale

Puoi usare la regola della catena con derivate parziali ? Naturalmente, la differenziazione parziale è proprio come la differenziazione regolare, solo che si presume che le altre variabili siano costanti, quindi la solita Regole derivate fare domanda a.

Quindi, si applica l'ideale della regola della catena multivariabile, solo che una variabile varia alla volta.

Integrazione della regola della catena

La Chain Rule nel senso di ciò che non si applica come strumento derivato, ma diventa invece un prezioso strumento di integrazione per sostituzioni e cambio di variabili.

Può essere concepito come una sorta di regola della catena inversa.

Esempio: utilizzo della regola della catena

Calcola la derivata della funzione: \(f(x) = \sin(\cos(x)) \)

Soluzione: Consideriamo la funzione \(\displaystyle f(x)=\sin\left(\cos\left(x\right)\right)\). Questa funzione corrisponde alla composizione di due funzioni: sin(x) e cos(x), per cui in questo caso si applicherebbe la regola della catena.

Qual è la conclusione : Possiamo concludere che la derivata che stiamo cercando è:

\[f'(x) = -\cos\left(\cos\left(x\right)\right)\sin\left(x\right)\]

e questo conclude il calcolo.

Esempio di regola a catena

Utilizzando la regola della catena e qualsiasi altra regola derivata, calcola: \(\displaystyle \frac{d}{dx} \left( \cos(x^2) \right)^2\)

Soluzione: In questo esempio abbiamo la funzione \(\displaystyle f(x)=\cos\left(x^2\right)\), che corrisponde a una funzione composta, che indica che la regola della catena è la regola della derivata corretta con cui iniziare (saranno necessarie altre regole lungo i calcoli)

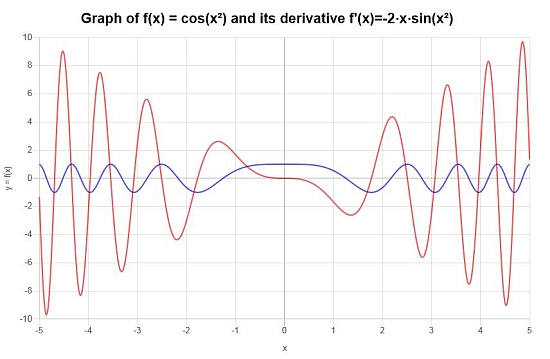
Derivata Finale : La conclusione è che la derivata della funzione fornita è data da:

\[f'(x) = -2x\sin\left(x^2\right)\]

Possiamo costruire la seguente rappresentazione grafica sull'intervallo \([-5, 5]\):

Esempio: un altro calcolo della regola della catena

Calcolare la derivata di \( f(x) = x^2 \sin(x^2)\) utilizzando la regola della catena.

Soluzione:

E' stata fornita la seguente funzione: \(\displaystyle f(x)=x^2\sin\left(x^2\right)\), per la quale dobbiamo calcolare la sua derivata.

La funzione è già stata semplificata, quindi possiamo procedere direttamente al calcolo della sua derivata:

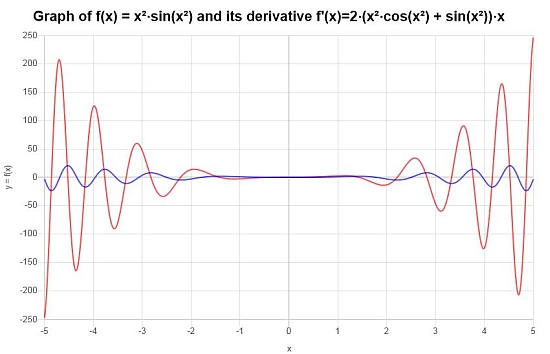
Qual è la conclusione finale : La conclusione finale è che la derivata che stiamo cercando è data da:

\[f'(x) = 2\left(x^2\cos\left(x^2\right)+\sin\left(x^2\right)\right)x\]

Graficamente abbiamo:

Altri calcolatori derivati

Sicuramente utilizzando un calcolatore derivato renderà le cose più facili quando si ha a che fare con funzioni piuttosto complicate. Il processo di differenziazione si allarga facilitato dall'uso di comuni, facili da ricordare Regole derivate , includendo il Regola Del Prodotto , il Regola Del Quoziente e il Regola Di Derivazione .

Queste regole ti aiuteranno a gestire ogni funzione differenziabile, ma il processo algebrico del calcolo e semplificazione potrebbe non essere necessariamente facile.