Informazioni su questo calcolatore di linee tangenti

Questa calcolatrice ti consentirà di eseguire senza problemi i calcoli necessari per ottenere la tangente di una funzione, in un dato punto, mostrando tutti i passaggi.

Tutto quello che devi fare è fornire una funzione valida f(x) e un punto in cui vuoi che si trovi la linea tangente. La funzione potrebbe essere qualsiasi funzione valida e differenziabile come f(x) = sin(x) o f(x) = x^2 - x + 1, ecc. Il punto può essere qualsiasi espressione numerica valida, come 1/2 per esempio.

Quindi, quando le informazioni richieste sono state fornite ed è valida, è necessario fare clic su "Calcola" per visualizzare tutti i passaggi dell'equazione della linea tangente.

Le applicazioni della linea tangente abbondano nella scienza ovunque. Chiamato anche primo ordine o approssimazione lineare , ha un significato davvero profondo in fisica e ingegneria, dove l'idea del contributo principale al cambiamento (la parte di primo ordine) è quella che svela molte informazioni su un processo.

Qual è la retta tangente

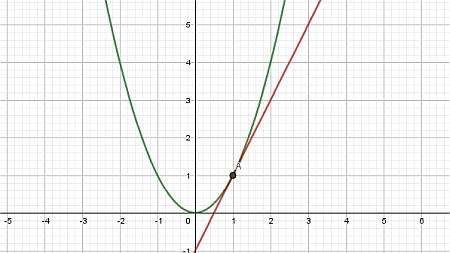
In termini semplici, una linea tangente è una linea che interseca una curva, ma la interseca solo in un punto (almeno localmente). Questa linea tangente è costruita fissando un punto \(x_0\) e poi prendendo un altro punto \(x_1\).

Quindi, costruendo la retta che passa per i punti \((x_0, f(x_0))\) e \((x_1, f(x_1))\), si ottiene quello che si chiama a Linea secante , come mostrato nel grafico sottostante:

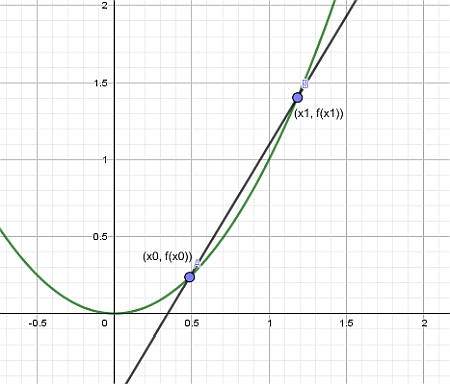
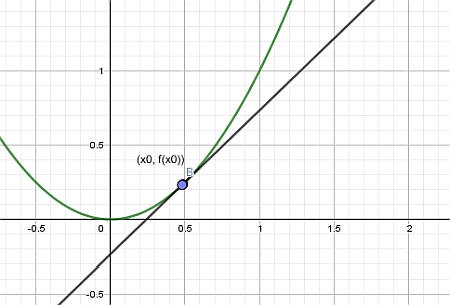
Infine, lasciamo che il punto \(x_1\) si avvicini a \(x_0\), e ciò che otteniamo è la retta tangente:

Passaggi per trovare geometricamente la retta tangente

• Passo 1: Identifica la funzione f(x) con cui vuoi lavorare e il punto x0. Ti servono entrambi
• Passo 2: Il punto (x0, f(x0)) sarà sulla curva della funzione f(x). Traccialo
• Passaggio 3: Scegli un punto (x1, f(x1)), per un x1 diverso da x0 (può essere a sinistra oa destra di x). Traccialo
• Passaggio 4: Disegna una linea che passa per i punti (x0, f(x0)) e (x1, f(x1))
• Passaggio 5: Scegli un punto x2 che si trovi a metà tra x0 e x1 e traccia una linea passante per i punti (x0, f(x0)) e (x2, f(x2))
• Passaggio 6: Ripeti questo processo alcune volte

Questo metodo grafico ti aiuterà a farti un'idea approssimativa di come appare la linea tangente, ma è un'approssimazione (a meno che la funzione f(x) non sia lineare).

Formula della retta tangente

Il metodo di approssimazione che utilizza le rette secanti può darti un'idea di ciò che stai cercando, ma fortunatamente esiste una formula esatta per calcolare la retta tangente a una funzione in un punto \(x_0\). La formula della retta tangente è:

\[\displaystyle y = f(x_0) + f'(x_0) (x - x_0) \]

Semplice, eh? In termini semplici, questa formula dice che la retta tangente è a retta che passa per il punto \((x_0, f(x_0))\) e che ha una pendenza di \(m = f'(x_0)\)

Allora, in termini semplici, la pendenza della retta tangente in un dato punto è esattamente la derivata della funzione in quel punto.

Passaggi per l'applicazione della formula della retta tangente

• Passo 1: Identificare la funzione f(x) e il punto x0
• Passo 2: Calcola il valore della funzione in x0, che è f(x0)
• Passaggio 3: Calcola la derivata di f(x) nel punto x0, quindi hai bisogno di f'(x0)
• Passaggio 4: Applica direttamente la formula della retta tangente \(y = f(x_0) + f'(x_0) (x - x_0)\)

Una volta che hai il equazione della retta , puoi trasformarlo nel formato più utile alla situazione in questione.

La pendenza della retta tangente

Uno dei punti chiave è che la pendenza della retta tangente in \(x_0\) è esattamente \(f'(x_0)\), che è la derivata nel punto \(x_0\). Ciò fornisce un'interpretazione chiara ed estremamente utile della derivata in termini geometrici.

Questa connessione permette di trovare l'equazione della retta tangente ad una data curva in un dato punto semplicemente guardando la derivata della funzione.

Quando hai una linea tangente orizzontale?

Una linea tangente orizzontale si verificherà quando il punto scelto \(x_0\) quando la derivata corrispondente in quel punto è uguale a zero. In tal caso la linea tangente (che è la linea che tocca la curva in un punto localmente) sarà parallela all'asse y.

Quindi, tutto ciò che devi sapere per identificare le linee tangenti orizzontali è trovare i punti in cui la derivata della funzione è zero.

Quando hai una tangente verticale?

Una linea tangente verticale si verificherà quando la derivata è "infinita" in un punto. Questo è un modo semplice per dire che è dove la derivata non è definita in un dato punto, ma converge all'infinito man mano che ci avviciniamo al punto.

Ad esempio, si potrebbe dire che \(f(x) = \frac{1}{x}\) ha una linea tangente verticale in x = 0. Tuttavia, si potrebbe sostenere che non esiste una linea tangente perché la derivata non è ben definita in x = 0.

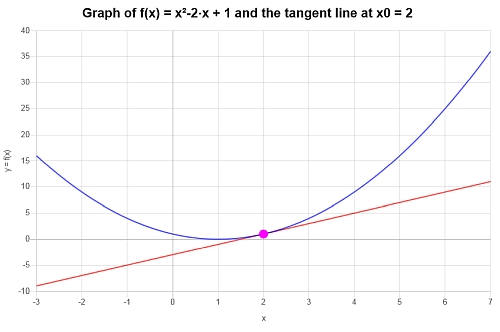
Esempio: linea tangente

Trova l'equazione della retta tangente per \(f(x) = x^2 - 2x + 1\), nel punto \(x_0 = 2\).

Soluzione: La seguente funzione è quella con cui dobbiamo lavorare: \(\displaystyle f(x)=x^2-2x+1\). Per prima cosa dobbiamo calcolare la sua derivata.

La funzione è già stata semplificata, quindi possiamo procedere direttamente al calcolo della sua derivata:

Linea Tangente : L'equazione della retta tangente per la funzione \(\displaystyle f(x)=x^2-2x+1\) nel punto \(x_0 = 2\) è:

\[y = y_0 + f'(x_0)(x - x_0) \]

In questo caso, \(\displaystyle y_0 = f(x_0)\), quindi inserire il valore del punto \(x_0 = 2\) nella funzione porta a:

\[y_0 = f(x_0) = f(2) = 2^2-2\cdot 2+1 = 1 \]

Inoltre, collegando il valore del punto \(x_0 = 2\) alla derivata calcolata si ottiene:

\[f'(x_0) = f'(2) = 2\cdot 2-2 = 2 \]

Quindi, ora inseriamo questi valori nella formula della linea tangente per ottenere:

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 1+2\left(x-2\right) = 2x-3 \]

Conclusione : Si trova quindi che la retta tangente per la funzione \(\displaystyle f(x)=x^2-2x+1\) nel punto \(x_0 = 2\) è:

\[y = 2x-3 \]

Si ottiene il seguente grafico per la funzione data e la sua retta tangente in \(x_0 = 2\):

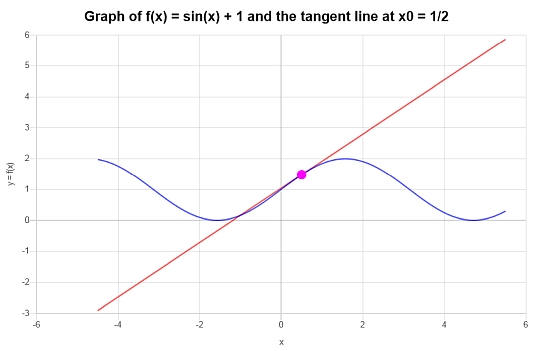
Esempio: equazione della retta tangente

Qual è la retta tangente in x = 1/2, per la funzione \(f(x) = \sin(x) + 1\)?

Soluzione:

E' stata fornita la seguente funzione: \(\displaystyle f(x)=\sin\left(x\right)+1\), per la quale dobbiamo calcolare la sua derivata.

La funzione è già stata semplificata, quindi possiamo procedere direttamente al calcolo della sua derivata:

Linea Tangente : Troviamo che la corrispondente equazione della retta tangente nel punto \(x_0 = \frac{1}{2}\) è data da:

\[y = y_0 + f'(x_0)(x - x_0) \]

Ma in questo caso specifico, \(\displaystyle y_0 = f(x_0)\), il che significa che dobbiamo collegare il valore del punto \(x_0 = \frac{1}{2}\) alla funzione, quindi otteniamo:

\[y_0 = f(x_0) = f\left(\frac{1}{2}\right) = \sin\left(\frac{1}{2}\right)+1\]

Ora, facendo lo stesso alla derivata, per \(x_0 = \frac{1}{2}\) troviamo

\[f'(x_0) = f'\left(\frac{1}{2}\right) = \cos\left(\frac{1}{2}\right) \]

Ora dobbiamo solo collegare i valori, quindi lo troviamo

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = \sin\left(\frac{1}{2}\right)+1+\cos\left(\frac{1}{2}\right)\left(x-\frac{1}{2}\right) = x\cos\left(\frac{1}{2}\right)-\frac{1}{2}\cos\left(\frac{1}{2}\right)+\sin\left(\frac{1}{2}\right)+1 \]

Conclusione : Troviamo che la retta tangente corrispondente che stiamo cercando, nel punto corrispondente \(x_0 = \frac{1}{2}\) è data da

\[y = x\cos\left(\frac{1}{2}\right)-\frac{1}{2}\cos\left(\frac{1}{2}\right)+\sin\left(\frac{1}{2}\right)+1 \]

Graficamente:

Esempio: un'altra linea tangente

Qual è la retta tangente in x = 0, per la funzione \(f(x) = \cos(x)\)? Ha senso questo risultato?

Soluzione: Osserva che \(f'(x) = -\sin(x)\), quindi \(f'(0) = -\sin(0) = 0\). Cioè, la retta tangente ha una pendenza di m = 0 in x = 0, quindi l'equazione della retta tangente è semplicemente \(y = y_0 = \cos(0) = 1\). Questo ha senso perché in questo caso la linea tangente è una linea orizzontale.

Altri calcolatori di differenziazione

Alcune persone potrebbero affermare che la differenziazione è un esercizio relativamente semplice e che l'utilizzo di a calcolatore derivato potrebbe non essere necessario, ma in verità il calcolo delle derivate può essere ancora piuttosto macchinoso e richiedere tempi lunghi calcoli algebrici .

Quando hai un'espressione con più di una variabile, per trovare la derivata dovrai determinare se le variabili sono indipendenti l'una dall'altra, nel qual caso usi derivate parziali , o se c'è un'equazione che collega le variabili nel qual caso dovresti usare Differenziazione implicita .

Le due aree principali del calcolo differenziale sono l'integrazione e la differenziazione, ed entrambe hanno le loro ampie applicazioni, ovunque. derivate parziali compaiono ampiamente nelle applicazioni di Ingegneria ed Economia.

Da un lato, la differenziazione si occupa di tassi di cambiamento infinitesimali, mentre l'integrazione si occupa di sommare tassi di cambiamento infinitesimali e, mirabilmente, sono strettamente collegati dal Teorema fondamentale del calcolo .