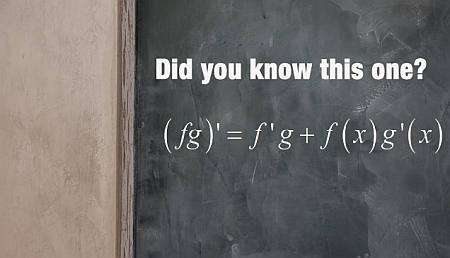Risolutori Calcolo

Regola del prodotto

Istruzioni: Usa questa calcolatrice quindi usa la Regola del prodotto, per differenziare una data funzione, mostrando tutti i passaggi. Digita la funzione di cui vuoi trovare la derivata nella casella sottostante.

Maggiori informazioni sulla regola del prodotto

Questo calcolatore ti aiuterà a trovare la derivata delle funzioni usando la regola del prodotto. Per utilizzare il calcolatore, è necessario fornire una funzione valida per la quale è coinvolto un prodotto.

Un esempio di una funzione valida potrebbe essere qualcosa come f(x) = x*sin(x), o qualcosa come g(x) = sin(x)*cos(x), solo per citarne alcuni.

Quindi, stiamo digitando la funzione per la quale desideri utilizzare la regola del prodotto, quindi devi fare clic su, tutto ciò che devi fare è fare clic sul pulsante "Calcola" e verranno forniti tutti i passaggi dei calcoli a te.

Una delle prime regole di derivata che imparerai è infatti la regola del prodotto, poiché la maggior parte delle funzioni che costruisci da funzioni elementari utilizzano il prodotto di funzioni.

Formula della regola del prodotto

Imparando regola derivata è forse il primo che farai quando imparerai a farlo trova la derivata di una funzione. E una delle prime regole che imparerai è senza dubbio la regola del prodotto.

La regola del prodotto, in parole povere, è una regola che ti aiuta a calcolare la derivata di un prodotto di funzioni. La formula della regola del prodotto è:

\[\displaystyle (f(x) g(x))' = f'(x) g(x) + f(x) g'(x) \]

Passaggi per l'utilizzo della regola del prodotto

Fase 1: Identifica chiaramente le funzioni f(x) e g(x) che formano il prodotto con cui stai lavorando
Passo 2: Apportare semplificazioni se necessario, mantenendo la struttura del prodotto
Smusso 3: Utilizzare la formula della regola del prodotto: \((f(x) g(x))' = f'(x) g(x) + f(x) g'(x) \) che consiste nel collegare il valore delle funzioni f(x) e g(x), nonché delle sue derivate f'(x) e g'(x)

Lavorando con una derivata della regola del prodotto, essenzialmente ottieni la derivata del prodotto in base alla conoscenza delle singole funzioni e delle loro derivate.

Quali altre regole derivate ci sono?

Oltre alla regola del prodotto, ci sono altre regole importanti come la regola di linearità, la Regola Del Quoziente che afferma che \(\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}\), e the Regola Di Derivazione , in cui si afferma che \(\frac{d}{dx} f(g(x)) = f'(g(x))g'(x)\).

Troverai anche altre regole menzionate in giro, come la regola di potenza, che indica che \(\frac{d}{dx} x^n = n x^{n-1}\), per una costante \(n\).

Suggerimenti e trucchi

La regola del prodotto può essere considerata come una regola di moltiplicazione derivata e la regola del prodotto gioca un ruolo cruciale in Calculus, quindi vale la pena impararla bene.

Si noti che nel caso di funzioni multivariabili, è possibile utilizzare la regola della moltiplicazione di matrici, per operare la regola del prodotto.

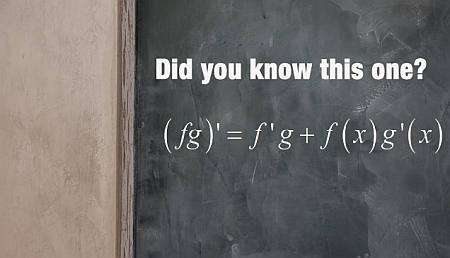
Esempio: utilizzo della regola del prodotto

Calcola la derivata di: \(f(x) = (x-1)(2x+1) \)

Soluzione: Consideriamo la seguente funzione \(\displaystyle f(x)=\left(x-1\right)\left(2x+1\right)\), che deve essere differenziata.

\( \displaystyle \frac{d}{dx}\left(\left(2x+1\right)\left(x-1\right)\right)\)

By using the Product Rule: \(\frac{d}{dx}\left( \left(2x+1\right)\left(x-1\right) \right) = \frac{d}{dx}\left(2x+1\right) \cdot \left(x-1\right)+\left(2x+1 \right) \cdot \frac{d}{dx}\left(x-1\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(2x+1\right) \cdot \left(x-1\right)+\left(2x+1 \right) \cdot \frac{d}{dx}\left(x-1\right)\)

By linearity, we know \(\frac{d}{dx}\left( x-1 \right) = \frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\) and \(\frac{d}{dx}\left( 2x+1 \right) = \frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \left(\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(1\right)\right) \left(x-1\right)+\left(2x+1 \right) \left(\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\right)\)

Since the derivative of a constant is 0, we find that:

\( \displaystyle = \,\,\)

\(\displaystyle \left(\frac{d}{dx}\left(2x\right)\right) \left(x-1\right)+\left(2x+1 \right) \left(\frac{d}{dx}\left(x\right)\right)\)

It is known that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(\frac{d}{dx}\left(2x\right)\right) \left(x-1\right)+\left(2x+1 \right)\)

So, we directly get: \(\frac{d}{dx}\left( 2x \right) = 2\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(2\right) \left(x-1\right)+\left(2x+1 \right)\)

and then we find

\( \displaystyle = \,\,\)

\(\displaystyle 2x+1+2\left(x-1\right)\)

Note that \((2) \cdot (x-1) = 2x-2\cdot 1 = 2x-2\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle 2x+1+2x-2\)

Grouping the terms with \(x\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(2+2\right)x+1-2\)

Grouping together numerical values and operating the terms that were grouped with \(x\)

\( \displaystyle = \,\,\)

\(\displaystyle 4x+1-2\)

Reducing the integers that can be subtracted together: \(\displaystyle 1-2 = -1\)

\( \displaystyle = \,\,\)

\(\displaystyle 4x-1\)

Conclusione : Pertanto, si conclude che la derivata della funzione è:

\[f'(x) = 4x-1\]

Graficamente, la seguente trama rappresenta la situazione:

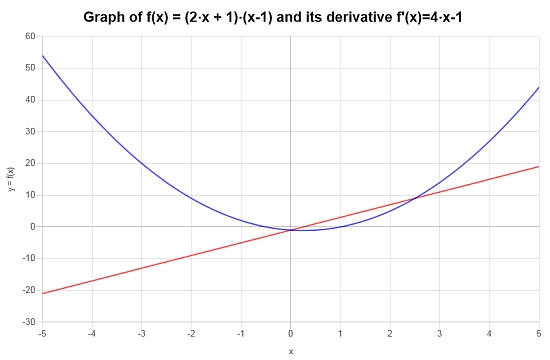
Esempi di regole del prodotto

Trova la derivata di: \(f(x) = x \sin(x)\)

Soluzione: In questo esempio la funzione data è \(\displaystyle f(x)=x\sin\left(x\right)\). Troviamo la sua derivata

\( \displaystyle \frac{d}{dx}\left(x\sin\left(x\right)\right)\)

Usiamo la regola del prodotto: \(\frac{d}{dx}\left( x\sin\left(x\right) \right) = \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)\)

Differenziando direttamente troviamo: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \cos\left(x\right)\)

Quindi dopo aver semplificato otteniamo che:

\( \displaystyle = \,\,\)

\(\displaystyle x\cos\left(x\right)+\sin\left(x\right)\)

Conclusione : Quindi, troviamo che la derivata è data dalla seguente formula:

\[f'(x) = x\cos\left(x\right)+\sin\left(x\right)\]

Il seguente grafico è costruito per la funzione e la sua derivata:

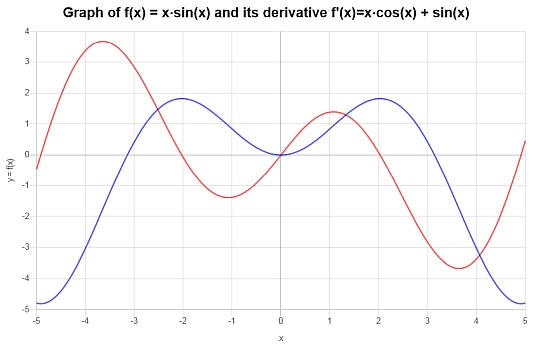
Esempio: un altro calcolo della regola del prodotto

Differenziare la seguente funzione \( f(x) = x (x+1)^2 \).

Soluzione: Infine, per questo esempio la funzione data è \(\displaystyle f(x)=x\left(x+1\right)^2\). Poiché esiste un prodotto di funzione, possiamo usare la regola del prodotto per la differenziazione.

\( \displaystyle \frac{d}{dx}\left(\left(x+1\right)^2x\right)\)

Usiamo la regola del prodotto: \(\frac{d}{dx}\left( \left(x+1\right)^2x \right) = \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2 \cdot \frac{d}{dx}\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2 \cdot \frac{d}{dx}\left(x\right)\)

Sappiamo che \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2 \)

Utilizzo della regola di potenza per un esponente costante: \(\frac{d}{dx}\left( \left(x+1\right)^2 \right) = 2x+1\cdot \frac{d}{dx}\left(x+1\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(2x+1\cdot \frac{d}{dx}\left(x+1\right)\right) x+\left(x+1\right)^2 \)

Per linearità, conosciamo \(\frac{d}{dx}\left( x+1 \right) = \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)\), quindi collegandolo:

\( \displaystyle = \,\,\)

\(\displaystyle \left(2x+1\left(\frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)\right)\right) x+\left(x+1\right)^2 \)

La derivata di una costante è 0, quindi:

\( \displaystyle = \,\,\)

\(\displaystyle \left(2x+1\left(\frac{d}{dx}\left(x\right)\right)\right) x+\left(x+1\right)^2 \)

Sappiamo che \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(2x+1\right) x+\left(x+1\right)^2 \)

che poi porta a

\( \displaystyle = \,\,\)

\(\displaystyle \left(x+1\right)^2+2\left(x+1\right)x\)

Espandendo i termini: \(\left(x+1\right)^2 = \left(x+1\right)\left(x+1\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(x+1\right)\left(x+1\right)+2\left(x+1\right)x\)

Osserviamo che \((x+1) \cdot (x+1) = x^2+1x+1x+1^2 = x^2+2x+1\), in quanto possiamo utilizzare la proprietà distributiva su ogni termine dell'espressione a sinistra, rispetto ai termini a destra

\( \displaystyle = \,\,\)

\(\displaystyle x^2+2x+1+2\left(x+1\right)x\)

Si noti che \((x+1) \cdot (x) = x^2+1x = x^2+x\), per il fatto che possiamo usare la proprietà distributiva su ogni termine dell'espressione a sinistra, rispetto ai termini a destra

\( \displaystyle = \,\,\)

\(\displaystyle x^2+2x+1+2\left(x^2+x\right)\)

Otteniamo \((2) \cdot (x^2+x) = 2x^2+2x = 2x^2+2x\), utilizzando la proprietà distributiva su ogni termine dell'espressione a sinistra, rispetto ai termini a destra

\( \displaystyle = \,\,\)

\(\displaystyle x^2+2x+1+2x^2+2x\)

Raggruppamento dei termini con \(x\), \(x^2\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(2+2\right)x+\left(1+2\right)x^2+1\)

Mettendo insieme i numeri interi e semplificando i termini che sono stati raggruppati con \(x\), \(x^2\)

\( \displaystyle = \,\,\)

\(\displaystyle 4x+3x^2+1\)

Allora otteniamo

\( \displaystyle = \,\,\)

\(\displaystyle \left(3x+1\right)\left(x+1\right)\)

Conclusione : In base a quanto sopra calcolato, si trova che la derivata corrispondente è:

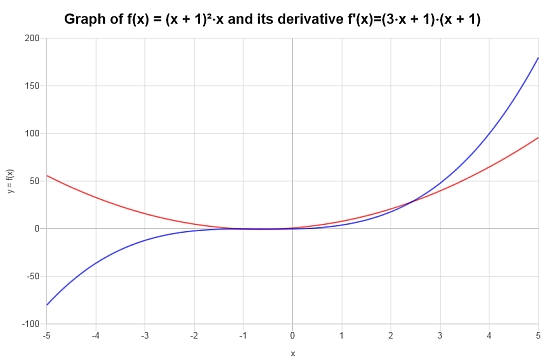
\[f'(x) = \left(3x+1\right)\left(x+1\right)\]

Si ottiene il seguente grafico per la data funzione sull'intervallo \([-5, 5]\):

Più calcolatori derivati

Poche persone non saranno d'accordo su questa differenziazione insieme all'integrazione e al punto centrale del calcolo. Calcolo di una derivata è un'abilità cruciale che dovrai imparare come studente di calcolo.

Puoi imparare diversi "sapori" di differenziazione, incluso differenziazione parziale così come Differenziazione implicita , che vengono utilizzati in diversi contesti applicativi.

Le applicazioni includono Linea tangente calcolo, che è lo stesso di a Approssimazione Lineare , così come l'uso di derivate di ordine superiore, a partire da derivate di secondo ordine .