Comment résoudre x

Cette calculatrice vous permettra de résoudre x pour n'importe quelle équation donnée, en affichant toutes les étapes du processus au cas où une solution pourrait être trouvée, ce qui n'est pas toujours le cas.

Vous pouvez fournir une expression telle que "y = x + 1", qui est une fonction linéaire simple où x apparaît, ou une expression plus complexe, telle que "x^2 + y^2 = 1", où vous aurez plus d'une solution.

Une fois que vous avez fourni une expression valide impliquant x, vous pouvez cliquer sur "Calculer" pour que le processus démarre, et la calculatrice tentera de résoudre x, par en résolvant l'équation nécessaires. Notez le mot "tenter", car vous constaterez que certaines équations ne peuvent pas être résolues.

Comment résous-tu pour x ?

Il n'y a pas vraiment de réponse unique à cette question, car cela dépend fortement de la structure de l'équation dans laquelle x apparaît. Les équations linéaires sont simples à traiter, car il suffit de déplacer les termes et de diviser l'égalité par un nombre si nécessaire.

Ou pour équations quadratiques vous obtiendrez un type de formule simple, la bien connue formule quadratique qui vous dira exactement comment résoudre x.

Mais pour tout ce qui est plus complexe, c'est un no man's land, et chaque équation nécessitera sa propre approche, s'il y en a une, pour être résolue.

C'est pourquoi le fait de disposer d'un calculatrice d'équations est si important, car il vous permettra de résoudre les types d'équations les plus courants et vous proposera des astuces à essayer en cas de difficulté, ce qui augmentera vos chances de réussite.

Étapes de la résolution de x

• Étape 1 : Tout d'abord, essayez d'identifier le type d'équation : linéaire, quadratique, polynomiale, rationnelle, radicale, logarithmique, exponentielle, etc.
• Étape 2 : Si vous avez identifié le type d'équation, il y aura des règles spécifiques à respecter pour résoudre ce type d'équation. Ex : si vous trouvez que l'équation pour x est exponentielle, l'astuce habituelle pour ce type d'équations est de définir une base commune et de mettre en équation les exposants afin de résoudre l'équation
• Étape 3 : Si aucun type d'équation spécifique n'a été identifié, vous pouvez simplement suivre une feuille de route générique : Essayez d'isoler tous les termes impliquant x d'un côté de l'équation (selon le type d'équation, cela peut ne pas être possible)
• Étape 4 : Pouvez-vous appliquer une substitution appropriée ? Pouvez-vous simplifier les choses en appliquant une fonction ou une opération aux deux côtés de l'égalité ? C'est à peu près le conseil général pour vous aider à démarrer

Honnêtement, c'est à peu près tout ce que vous pouvez savoir en règle générale pour résoudre des équations et trouver x. Le reste viendra de la structure spécifique de l'équation à laquelle vous avez affaire.

Il n'y a donc pas de formule pour x ?

Malheureusement, ce n'est pas le cas en général. Pour les types les plus faciles, vous pourrez trouver une formule pour x, quelque chose comme x = g(y), et parfois cette formule vous aidera à définir un Fonction inverse mais il arrive que vous ne trouviez aucune formule, ou que vous trouviez plus d'une solution.

Parfois, vous devrez restreindre les variables par résolution d'une inégalité afin de trouver une solution pour x. En effet, dans de tels cas, la résolution pour x ne réussit que dans une région restreinte.

Y a-t-il une différence entre la résolution de x et la résolution de y ?

Oui, du point de vue de la variable cible que vous voulez résoudre, mais non d'un point de vue méthodologique, car les mesures que vous prenez pour résoudre x sont les mêmes que celles que vous prendriez pour résoudre y.

La résolution de x, y ou z implique le même processus, à savoir la résolution d'une variable spécifique, qui requiert la même méthodologie. Dans certains cas, la symétrie joue un rôle, et c'est même littéralement la même chose. Pour le voir concrètement, si vous avez l'équation \(x^2+y^2=1\), la résolution de x conduira exactement aux mêmes étapes que la résolution de y. Cela n'est vrai que pour ce type d'équations symétriques.

Exemple : solve for x

Trouver x en termes de y pour : \(\frac{1}{3} y = \frac{x-1}{x+4} - \frac{5}{6}\)

Solution : Dans ce cas, il s'agit d'une simple équation linéaire. La résolution de x consiste donc à mettre x d'un côté :

\[\frac{1}{3} y = \frac{x-1}{x+4} - \frac{5}{6}\] \[ \Rightarrow \frac{1}{3} y = \frac{x-1}{x+4} - \frac{5}{6}\] \[ \Rightarrow \frac{1}{3} y + \frac{5}{6} = \frac{x-1}{x+4}\] \[ \Rightarrow \left( \frac{1}{3} y + \frac{5}{6} \right) (x+4) = x - 1\] \[ \Rightarrow x \left( \frac{1}{3} y + \frac{5}{6} \right) +4 \left( \frac{1}{3} y + \frac{5}{6} \right) = x - 1\] \[ \Rightarrow x \left( \frac{1}{3} y + \frac{5}{6} - 1\right) = - 1 - 4 \left( \frac{1}{3} y + \frac{5}{6} \right)\]

Ensuite, en manipulant les termes de l'équation ci-dessus, nous obtenons la solution :

\[x=-\frac{2\cdot \left(4y+13\right)}{2y-1} \]

Par conséquent, la résolution de \(x\) pour l'équation donnée conduit à la solution \(x=-\frac{2\cdot \left(4y+13\right)}{2y-1}\).

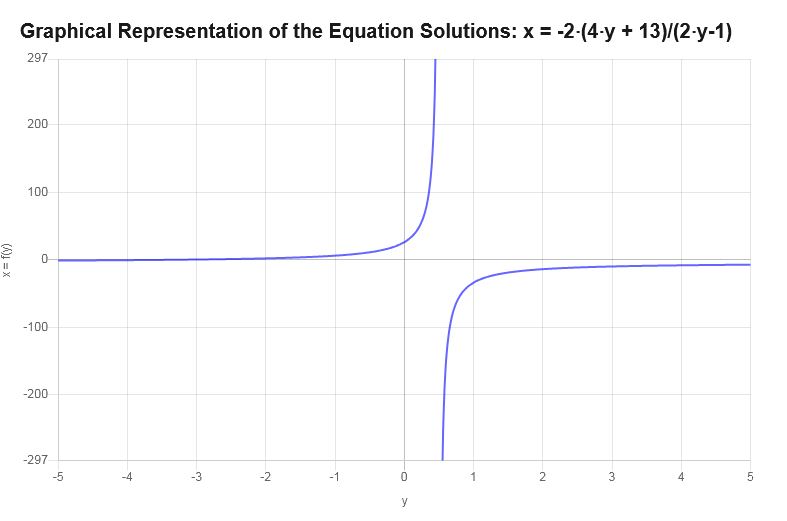
Graphiquement

Voici la représentation graphique des solutions obtenues avec \(y\) exprimées en termes de \(\) :

Exemple : pouvez-vous résoudre x ?

Pouvez-vous résoudre x dans ce cas : \(y = x^2 - 1\)

Solution : Dans ce cas, nous obtenons directement que

\[y = x^2 - 1 \Rightarrow x^2 = y + 1\] \[ \Rightarrow x = \pm \sqrt{ y + 1 }\]

Cela implique que nous sommes en mesure de trouver deux solutions, ou "branches", qui sont \(x = \sqrt{ y + 1 }\) et \(x = -\sqrt{ y + 1 }\).

Autres calculatrices d'équations utiles

Comme nous l'avons vu, la résolution de x s'appuie fortement sur les éléments suivants Résolution d'équations ce qui peut certainement constituer un défi pour les types d'équations plus complexes qui ne sont pas des équations linéaires ou quadratiques.

L'idée de résoudre x est étroitement liée à la notion de trouver l'inverse et aussi trouver le graphique de l'inverse car c'est précisément ainsi que l'on commence lorsqu'il s'agit d'inverses.

Les équations peuvent devenir plus compliquées lorsqu'il s'agit d'équations simultanées, qui nécessitent des techniques spécifiques. Une procédure courante à laquelle nous pouvons avoir recours est la suivante Résolution de systèmes d'équations linéaires en utilisant des méthodes graphiques ou analytiques