En savoir plus sur le graphique des fonctions inverses

Cette calculatrice vous aide à trouver le graphique de la fonction inverse que vous lui fournissez, à condition que la fonction ait une inverse, ce qui n'est pas toujours le cas.

Vous pouvez fournir une fonction sous la forme "y = 2x - 1", ou simplement une expression telle que "f(x) = (x-1)/(x-3)" ou simplement "(x-1)/(x-3)" pour spécifier la fonction.

Une fois que vous avez fourni une fonction valide, vous pouvez cliquer sur le bouton "Calculer", et vous verrez toutes les étapes du processus de calcul calcul de la fonction inverse et si l'inverse existe, un graphique de la fonction et de l'inverse sera représenté.

Observez que pour que la fonction donnée ait une fonction inverse, la fonction doit être biunivoque, ce qui signifie que chaque valeur dans l'intervalle de la fonction a au plus une pré-image dans le domaine de la fonction, et exactement une pré-image dans l'intervalle effectif restreint.

Comment savoir si une fonction est inversible

Avant d'obtenir le graphique de l'inverse d'une fonction donnée, vous devez savoir si la fonction a un inverse. Le principal critère pour avoir une inverse est d'être biunivoque, ce qui signifie qu'une valeur dans l'intervalle ne peut pas avoir deux valeurs associées (images préalables).

Il est possible que les élèves préfèrent ne pas utiliser des termes techniques tels que "images" et "préimages", et bien qu'il s'agisse de concepts fondamentaux de la théorie des fonctions, nous pouvons dans ce cas utiliser un simple test graphique pour évaluer si une fonction est biunivoque ou non, et donc si vous pouvez trouver et représenter graphiquement son inverse.

Test de la ligne horizontale

Le test de la ligne horizontale indique que pour qu'une fonction soit biunivoque, toute ligne horizontale que vous construisez doit croiser le graphique de la fonction au plus une fois. Si vous parvenez à trouver une ligne horizontale qui traverse le graphique de la fonction donnée plus d'une fois, alors la fonction N'EST PAS biunivoque.

Par exemple, la fonction illustrée ci-dessous est biunivoque, car quelle que soit la ligne horizontale que l'on lance, elle traversera le graphique de la fonction exactement une fois :

Mais l'exemple suivant montre une fonction qui n'est pas biunivoque, car nous voyons une ligne horizontale qui croise la ligne de la fonction 2 fois (plus d'une fois) :

Etapes pour trouver le graphe inverse

• Étape 1 : Il existe deux méthodes courantes : la méthode graphique et la méthode analytique
• Étape 2 : Pour la méthode graphique, vous devez d'abord appliquer le test de la ligne horizontale et vous assurer qu'il est réussi, donc qu'il est biunivoque et que l'inverse existe
• Étape 3 : Ensuite, vous tracez la ligne y = x dans le graphique (une ligne droite qui a un angle de 45°) ^o degrés par rapport à l'axe des x
• Étape 4 : Il suffit ensuite d'utiliser la droite y = x comme "miroir" et de réfléchir les points du graphique original par rapport au "miroir". Le graphique obtenu grâce à ce processus de réflexion est le graphique de l'inverse de
• Étape 5 : Pour la méthode analytique, il faut d'abord algébroser trouver l'inverse : Vous commencez par y = f(x) et vous résolvez ensuite y.
• Étape 6 : S'il n'y a qu'une seule solution, alors la fonction inverse existe et vous l'écrivez x = g(y). En ajustant les noms des variables, vous définissez formellement la fonction inverse \(f^{-1}\) en termes de g
• Étape 7 : Enfin, vous représentez graphiquement l'inverse que vous avez trouvé \(f^{-1}\) comme vous le feriez représenter graphiquement une fonction normalement

Lorsque vous devez trouver le graphique d'une fonction inverse, les méthodes graphique et analytique conviennent toutes les deux. Seule la méthode analytique présente un avantage : vous calculez la fonction inverse tout au long du processus, ce qui vous permet d'obtenir une expression mathématique de la fonction, et pas seulement son graphique.

Pourquoi représenter graphiquement l'inverse

Il y a de nombreuses raisons de faire cela. Tout d'abord, la fonction inverse est en soi un acteur très important de la théorie des fonctions, car une fonction montre comment passer d'un x à un y. Il est donc naturel de vouloir connaître le mécanisme qui permet de passer de y à x, et c'est précisément ce que la fonction inverse vous fournit.

On peut donc considérer une fonction comme une carte à sens unique allant d'un point "X" à un point "Y", et calculer la fonction inverse revient à définir explicitement une carte pour aller de "Y" à "X".

Le graphique de l'inverse vous fournira de nombreuses informations sur cette fonction inverse : descend-elle, monte-t-elle, comment se comporte-t-elle ?

Comment cette calculatrice de fonctions graphiques inverses peut-elle m'aider ?

Tout d'abord, cette calculatrice analysera la fonction pour voir si elle est inversible en utilisant la méthode analytique, et s'il est possible de trouver cette inverse, elle la représentera graphiquement pour vous.

Pour trouver l'inverse, il faut résolution d'une équation ce qui n'est pas une tâche facile, à moins que vous n'ayez affaire à des Équations linéaires ou équations polynomiales mais à part cela, le processus peut s'avérer très complexe, voire impossible.

D'autres calculateurs peuvent effectuer un processus similaire, mais l'un des avantages de cette calculatrice est qu'il fournit toutes les étapes du processus, avec une explication détaillée, dans la mesure du possible.

Exemple : trouver le graphique de l'inverse

Représentez graphiquement l'inverse de : \( y = \frac{2}{3} x - \frac{5}{6}\)

Solution :

Nous avons reçu la fonction suivante :

\[ y = \frac{2}{3} x - \frac{5}{6}\]

Ensuite, pour trouver l'inverse de la fonction donnée, nous devons résoudre \(x\) et déterminer s'il y a une solution ou non. L'équation de départ est

\[y=\frac{2}{3}x-\frac{5}{6}\]

Étape 0 : Dans ce cas, nous devons d'abord simplifier l'équation linéaire donnée, et pour ce faire, nous procédons aux étapes de simplification suivantes :

Résolution de l'équation linéaire

En plaçant \(x\) du côté gauche et \(y\) et la constante du côté droit, nous obtenons

\[\displaystyle -\frac{2}{3}x = -y -\frac{5}{6}\]

Maintenant, en résolvant \(x\), en divisant les deux côtés de l'équation par \(-\frac{2}{3}\), on obtient ce qui suit

\[\displaystyle x=-\frac{1}{-\frac{2}{3}}y-\frac{\frac{5}{6}}{-\frac{2}{3}}\]

et en simplifiant on obtient finalement ce qui suit

\[\displaystyle x=\frac{3}{2}y+\frac{5}{4}\]

Par conséquent, la résolution de \(y\) pour une équation linéaire donnée conduit à \(x = \frac{3}{2}y+\frac{5}{4}\).

Par conséquent, et puisqu'en résolvant \(x\) nous trouvons une solution et qu'il s'agit d'une seule solution, nous avons trouvé l'inverse.

La fonction inverse trouvée

Sur la base des travaux présentés ci-dessus, on peut conclure que la fonction inverse est :

\[f^{-1}(x) = \frac{3}{2}x+\frac{5}{4}\]

La fonction inverse peut être représentée graphiquement comme suit :

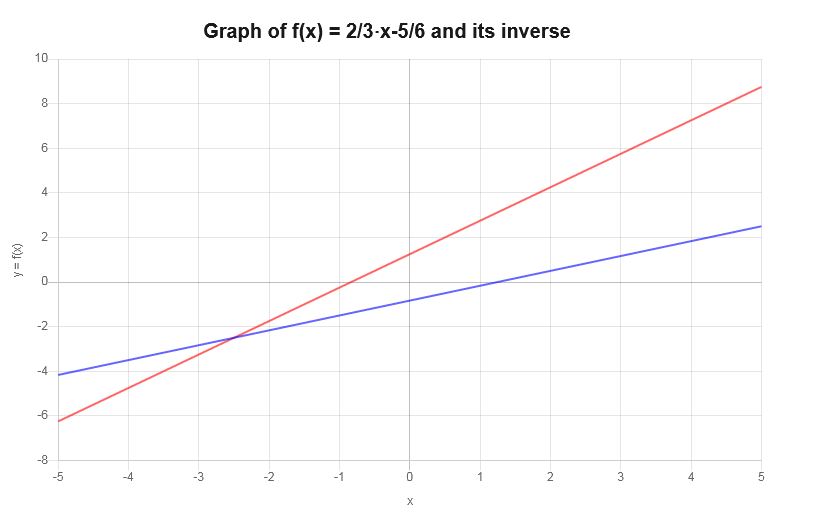
Exemple : autres graphes inverses

Pouvez-vous trouver le graphique inverse de : \(y = x^2\)

Solution : Non, nous ne pouvons pas trouver le graphe inverse de \(y = x^2\), car cette fonction ne passe pas le test de la ligne horizontale. Une autre façon de voir les choses est qu'en résolvant \(x\), nous obtenons \(x = \pm \sqrt y\), et comme nous trouvons deux solutions, il n'y a pas d'inverse, et par conséquent, il n'y a pas de graphe inverse.

Plus de calculatrices de fonctions

Les fonctions et tous les types d'opérations sur les fonctions sont véritablement au centre de l'algèbre et du calcul. Un bon Calculatrice de fonctions vous facilitera la tâche pour réduire une fonction à sa plus simple expression.

Ensuite, vous aurez une bonne outil de représentation graphique des fonctions afin de jeter un coup d'œil rapide aux propriétés graphiques d'une fonction. Voir le graphique d'une fonction peut vous en apprendre beaucoup sur son comportement, avant même de regarder son expression algébrique.

Il y a ensuite des opérations plus avancées, comme la recherche de la dérivée, pour laquelle voici Calculatrice de différentiation vous sera utile, car il vous montre toutes les étapes du processus. Comme prévu, la dérivée de la fonction inverse a une association intéressante avec la dérivée de la fonction originale.