Solveurs Calculus

Dérivés trigonométriques inverses

Instructions: Utilisez cette calculatrice pour trouver les dérivées des fonctions trigonométriques inverses, en montrant toutes les étapes. Veuillez saisir la fonction qui contient une fonction trigonométrique inverse dans la zone de formulaire ci-dessous.

Dérivés trigonométriques inverses

Avec cette calculatrice, vous pourrez calculer les dérivées des fonctions trigonométriques inverses, en montrant toutes les étapes du processus.

L'idée est que la fonction que vous fournissez contient une fonction trigonométrique inverse, par exemple f(x) = x^2/arctan(x+1), juste pour donner un exemple.

Lorsque vous êtes prêt et que vous avez fini de taper la fonction que vous devez différencier, cliquez sur le bouton "Calculer" afin de voir toutes les étapes du processus et les calculs.

L'idée de calcul des dérivées des fonctions trigonométriques inverses est naturelle, et nous verrons dans les paragraphes suivants qu'elles peuvent être directement dérivées de la dérivés trigonométriques que vous connaissez.

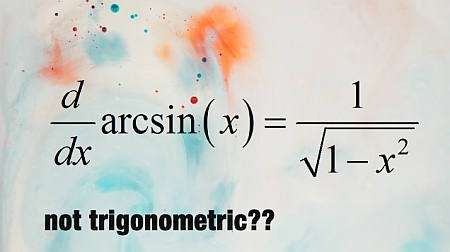
Fonctions de déclenchement inverses

En termes simples, les fonctions trigonométriques inverses sont les fonctions qui, en les évaluant à la fonction trigonométrique correspondante, conduisent à l'identité. Par exemple, si nous considérons la fonction \(\sin(x)\), sa fonction inverse est \(\arcsin(x)\), et cette inverse a la propriété que

\[\sin(\arcsin(x)) = x \]

aussi bien que

\[\arcsin(\sin(x)) = x \]

pour tout \(x\) sur un certain intervalle. Donc strictement, \(\arcsin(x)\) est la fonction inverse de \(\sin(x)\) d'un point de vue algébrique. Et il en va de même pour les autres fonctions trigonométriques inverses et leurs fonctions trigonométriques correspondantes.

Calcul des dérivées trigonométriques inverses

Alors, si \(f\) est une fonction, et qu'elle a un inverse \(f^{-1}\), alors on a ça

\[f^{-1}(f(x)) = x\]

pour tous \(x\). Ensuite, si nous différencions les deux côtés de l'égalité et que nous utilisons la règle de la chaîne sur le côté gauche, nous obtenons

\[ \displaystyle (f^{-1})'(f(x))f'(x) = 1\] \[ \displaystyle (f^{-1})'(f(x)) = \frac{1}{f'(x)}\]

Maintenant, si nous définissons \(y = f(x)\), alors \(x = f^{-1}(y)\), ce qui conduit à

\[ \displaystyle (f^{-1})'(y) = \frac{1}{f'(f^{-1}(y))}\] \[ \Rightarrow \displaystyle (f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))}\]

Comment l'utilisons-nous pour les fonctions trigonométriques inverses ? Supposons \(f(x) = \sin(x)\) et \(f^{-1}(x) = \arcsin(x)\). Alors, selon la relation générale entre la dérivée d'une fonction et la dérivée de son inverse, on obtient

\[ \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{\frac{d}{dx}\sin (\arcsin(x))}\] \[ \Rightarrow \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{\cos(\arcsin(x))}\]

Mais une astuce géométrique soignée nous dit que

\[\cos(\arcsin(x)) = \sqrt{1 - \sin^2(\arcsin(x))} = \sqrt{1 - x^2} \]

ce qui implique que

\[ \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{ \sqrt{1 - x^2}}\]

Le reste des dérivées trigonométriques inverses est obtenu avec un argument similaire.

Quelles sont les 6 fonctions trigonométriques inverses de base ?

#1: \( \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{ \sqrt{1 - x^2}}\)
#2 : \( \displaystyle \frac{d}{dx} \arccos(x) = -\frac{1}{ \sqrt{1 - x^2}}\)
#3 : \( \displaystyle \frac{d}{dx} \arctan(x) = \frac{1}{1+x^2}\)
#4 : \( \displaystyle \frac{d}{dx} \operatorname{arccot}(x) = -\frac{1}{1+x^2}\)
#5 : \( \displaystyle \frac{d}{dx} \operatorname{arcsec}(x) = \frac{1}{x \sqrt{x^2-1}}\)
#6 : \( \displaystyle \frac{d}{dx} \operatorname{arccsc}(x) = -\frac{1}{x \sqrt{x^2-1}}\)

Chose intéressante, lors du calcul de la dérivée des fonctions trigonométriques inverses, aucune des dérivées trigonométriques inverses n'implique de fonctions trigonométriques ou de fonctions trigonométriques inverses.

Applications de la dérivée des fonctions trigonométriques inverses

Les fonctions trigonométriques et leurs dérivées, ainsi que les fonctions trigonométriques inverses et leurs dérivées font partie de l'inventaire des fonctions et opérations de base, utilisées comme blocs de construction, pour créer des fonctions plus complexes.

Bien que les fonctions trigonométriques apparaissent plus souvent dans les applications que les fonctions trigonométriques inverses, ces dernières ont également une place claire dans le calcul, en particulier lors de la différenciation et de l'utilisation de la méthode de décomposition des fractions partielles.

Conseils et astuces

N'oubliez pas que les dérivées des fonctions trigonométriques inverses peuvent être extrêmement utiles, en particulier lors de l'intégration de termes ayant un dénominateur quadratique.

De plus, il est facile de faire des erreurs lors du calcul des dérivées trigonométriques inverses par définition, vous pourriez certainement bénéficier de l'utilisation d'un calculatrice de dérivées qui montrera les étapes, ou que vous pouvez utiliser pour vérifier votre travail.

Exemple : dérivés trigonométriques inverses

Calculez la dérivée de : \(f(x) = x + \arcsin(x^2)\)

Solution: Pour ce premier exemple, nous allons analyser \(\displaystyle f(x)=x+\arcsin\left(x^2\right)\). Cette fonction implique une fonction trigonométrique inverse, composée d'une autre fonction. Calculons sa dérivée :

\( \displaystyle \frac{d}{dx}\left(x+\arcsin\left(x^2\right)\right)\)

By linearity, we know \(\frac{d}{dx}\left( x+\arcsin(x^2) \right) = \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(\arcsin(x^2)\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(\arcsin\left(x^2\right)\right)\)

But we know already that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle 1+\frac{d}{dx}\left(\arcsin\left(x^2\right)\right)\)

By using the Chain Rule: \(\frac{d}{dx}\left( \arcsin\left(x^2\right) \right) = \frac{\frac{d}{dx}\left(x^2\right)}{\sqrt{1-\left(x^2\right)^2}}\)

\( \displaystyle = \,\,\)

\(\displaystyle 1+\frac{\frac{d}{dx}\left(x^2\right)}{\sqrt{1-\left(x^2\right)^2}}\)

In this case we use the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 1+\frac{2x}{\sqrt{1-\left(x^2\right)^2}}\)

which then leads to

\( \displaystyle = \,\,\)

\(\displaystyle 1+\frac{2x}{\sqrt{1-x^4}}\)

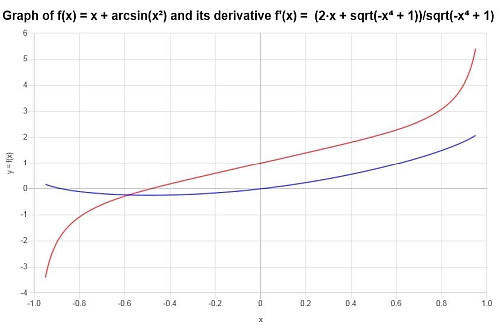
Répondre : Nous pouvons conclure que la dérivée de la fonction est :

\[f'(x) = \frac{2x+\sqrt{1-x^4}}{\sqrt{1-x^4}}\]

Nous pouvons voir à la fois la fonction et sa dérivée dans le graphique suivant :

Exemple : plus de dérivés trigonométriques inverses

Considérez la fonction suivante : \(f(x) = \frac{\arcsin(x)}{x}\), calculez sa dérivée.

Solution: Maintenant, pour le deuxième exemple, nous avons la fonction \(\displaystyle f(x)=\frac{\arcsin\left(x\right)}{x}\).

\( \displaystyle \frac{d}{dx}\left(\frac{\arcsin\left(x\right)}{x}\right)\)

The Quotient Rule applies in this case: \(\frac{d}{dx}\left( \frac{\arcsin\left(x\right)}{x} \right) = \frac{x \cdot \frac{d}{dx}\left(\arcsin\left(x\right)\right)-\arcsin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \frac{d}{dx}\left(\arcsin\left(x\right)\right)-\arcsin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}\)

We already know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \frac{d}{dx}\left(\arcsin\left(x\right)\right)-\arcsin\left(x\right)}{x^2}\)

Directly differentiating: \(\frac{d}{dx}\left( \arcsin\left(x\right) \right) = \frac{1}{\sqrt{1-\left(x\right)^2}}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \frac{1}{\sqrt{1-\left(x\right)^2}}-\arcsin\left(x\right)}{x^2}\)

and then we get

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\frac{1}{\sqrt{1-x^2}}x-\arcsin\left(x\right)}{x^2}\)

Finally, the following is obtained

\( \displaystyle = \,\,\)

\(\displaystyle \frac{-\left(\sqrt{1-x^2}\cdot \arcsin\left(x\right)-x\right)}{\sqrt{1-x^2}\cdot x^2}\)

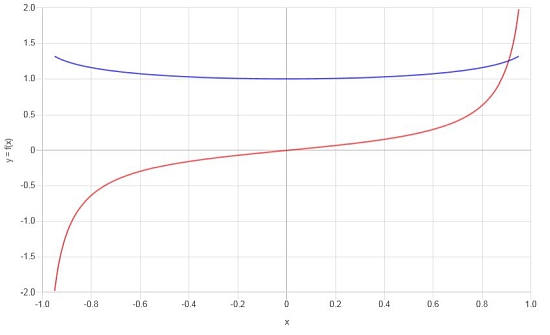
Conclusion Finale : La dérivée recherchée est :

\[f'(x) = \frac{-\left(\sqrt{1-x^2}\cdot\arcsin\left(x\right)-x\right)}{\sqrt{1-x^2}\cdot x^2}\]

Graphiquement, nous avons ceci :

Exemple de dérivés trigonométriques inverses

Calculez la dérivée de : \(f(x) = x \arctan(x+1)\)

Solution: Maintenant, pour ce dernier exemple, nous allons travailler avec la fonction \(\displaystyle f(x)=x\arctan\left(x+1\right)\), qui contient une fonction inverse.

\( \displaystyle \frac{d}{dx}\left(x\arctan\left(x+1\right)\right)\)

The Product Rule applies in this case: \(\frac{d}{dx}\left( x\arctan\left(x+1\right) \right) = \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{d}{dx}\left(\arctan\left(x+1\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{d}{dx}\left(\arctan\left(x+1\right)\right)\)

Using the Chain Rule: \(\frac{d}{dx}\left( \arctan\left(x+1\right) \right) = \frac{\frac{d}{dx}\left(x+1\right)}{1+\left(x+1\right)^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{\frac{d}{dx}\left(x+1\right)}{1+\left(x+1\right)^2}\)

By linearity, we know \(\frac{d}{dx}\left( x+1 \right) = \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{\frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)}{1+\left(x+1\right)^2}\)

The derivative of a constant is 0, so then:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{\frac{d}{dx}\left(x\right)}{1+\left(x+1\right)^2}\)

We know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{1}{1+\left(x+1\right)^2}\)

and then we get

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x\cdot 1}{1+\left(x+1\right)^2}+\arctan\left(x+1\right)\)

We expand the terms: \(\left(x+1\right)^2 = \left(x+1\right)\left(x+1\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x\cdot 1}{1+\left(x+1\right)\left(x+1\right)}+\arctan\left(x+1\right)\)

Reducing the one in \(x\cdot 1 = x\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x}{1+\left(x+1\right)\left(x+1\right)}+\arctan\left(x+1\right)\)

Finally, the following is obtained

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x^2\arctan\left(x+1\right)+2x\arctan\left(x+1\right)+x+2\arctan\left(x+1\right)}{x^2+2x+2}\)

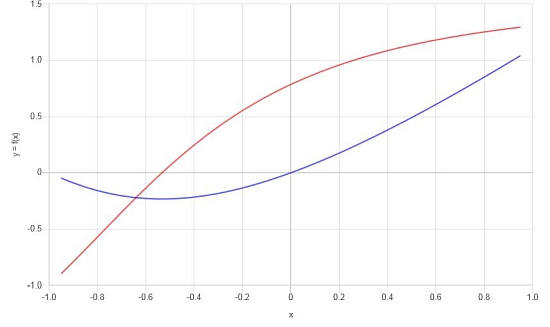
Conclusion : Après simplification, la dérivée est :

\[f'(x) = \frac{x^2\arctan\left(x+1\right)+2x\arctan\left(x+1\right)+x+2\arctan\left(x+1\right)}{x^2+2x+2}\]

Sur la base des résultats trouvés, nous pouvons construire le graphe suivant pour f et f' :

Autres calculatrices de calcul

Lors de l'utilisation dérivés trigonométriques , nous avons déclaré qu'il s'agissait d'éléments de base cruciaux pour l'application Règles relatives aux produits dérivés .

Les dérivés des fonctions trigonométriques inverses peuvent être dérivés simplement de la Produits Dérivés des dérivés trigonométriques basiques, et c'est pourquoi nous les considérons également dans le groupe des dérivés basiques à apprendre voire à mémoriser.