Estadísticas no paramétricas o qué hacer cuando fallan los supuestos de una prueba paramétrica

La media, la mediana y la moda son las medidas más comunes de tendencia central, que se utilizan para describir el centro de una distribución. De los tres, la media es la más utilizada, pero la mediana y la moda también se utilizan ampliamente.

Necesitamos distinguir entre el muestra media, mediana y moda, y su población contrapartes.

Normalmente, somos provisto de una muestra y necesitamos calcular la media muestral, la mediana muestral y la moda muestral. Estas estadísticas son estimadores de los parámetros poblacionales correspondientes.

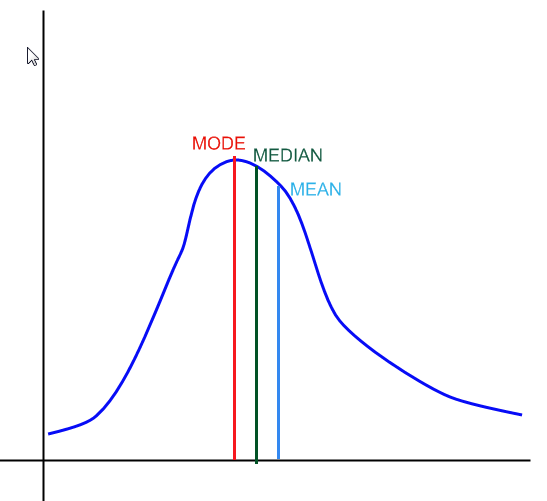
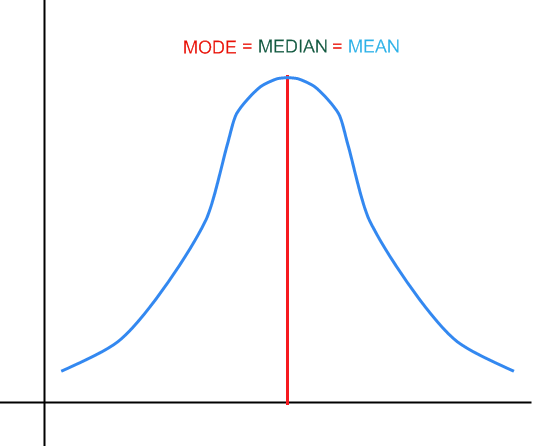
En el gráfico anterior, tiene un ejemplo de cómo se verían la mediana, la moda y la media en una distribución.

La moda corresponde al valor más repetido en una muestra. En una distribución, corresponde al punto más alto de la función de densidad, como se muestra en el gráfico anterior.

La mediana, aproximadamente, define el punto donde el 50% de la distribución se encuentra a su izquierda y a su derecha.

La media corresponde al promedio ponderado de los valores que toma la variable y sus probabilidades asociadas ($\sum x \cdot p(x)$). Para una distribución, dicha suma ponderada es una suma o una integral. Para una muestra, simplemente calculamos simplemente el promedio de valores en la muestra.

Cómo calcular la media, la mediana y la moda para una muestra dada

Ahora, suponga que se nos da una muestra $X_1, X_2, ..., X_n$, y queremos calcular la moda, la mediana y la media. ¿Cómo lo hacemos?

• Para el modo: Sencillo. Simplemente encontramos el número que se repite más. Ej: si tenemos una muestra 1, 2, 2, 2, 3, 1, 4, la moda es 2, porque 2 es el valor más repetido (se repite 3 veces)

• Para la mediana: Este cálculo es un poco más complicado. Tome su muestra $X_1, X_2, ..., X_n$ y el primer paso es reorganizarla en orden ascendente. Entonces, suponga que $\hat X_1, \hat X_2, ..., \hat X_n$ es la muestra después de reordenarla de los valores más bajos a los más altos.

Ahora, vamos a calcular la posición de la mediana en la muestra en orden ascendente. Para el tamaño de muestra $n$, calculamos $P = 0.5 (n+1)$.

Si este valor es un número entero, entonces encontramos que la mediana es el valor en la P ^th posición en la muestra en orden ascendente.

Si este valor NO es entero, entonces encontramos $P_L$ y $P_U$ que son los enteros más cercanos a la izquierda y derecha de $P$. (Ejemplo: si $P = 10.2$, entonces $P_L = 10$ y $P_U = 11$).

Entonces, la mediana es el promedio de los valores que están en las posiciones $P_L$ ^th y $P_U$ ^th en la muestra en orden ascendente. No se preocupe, lo practicaremos con un ejemplo.

• Para el medio: Sencillo también. La media de la muestra se calcula utilizando la fórmula

\[\displaystyle \frac{1}{n}\sum_{i=1}^n X_i\]

EJEMPLO 1

La media, la mediana y la moda para la siguiente muestra:

28, 36, 43, 30, 15, 19, 46, 36, 34, 38, 42, 29, 37, 35, 39, 39, 30, 39, 36, 38, 30, 41, 42, 46, 40, 33, 30, 40, 43, 12 42, 39, 30, 35, 38, 41, 30, 37, 40, 30, 30, 35, 39, 37, 42, 42, 37, 38, 32, 51

RESPONDEDOR:

La siguiente tabla muestra los cálculos necesarios para calcular la media

	Datos
	28
	36
	43
	30
	15
	19
	46
	36
	34
	38
	42
	29
	37
	35
	39
	39
	30
	39
	36
	38
	30
	41
	42
	46
	40
	33
	30
	40
	43
	12
	42
	39
	30
	35
	38
	41
	30
	37
	40
	30
	30
	35
	39
	37
	42
	42
	37
	38
	32
	51

Suma =	1791
Medios =	35,82

Por tanto, la media muestral es

\[\bar{X}=\frac{1}{n}\sum{{{X}_{i}}}=\frac{1791}{50}=35.82\]

Ahora, para la mediana, la siguiente tabla muestra los datos en orden ascendente:

Datos (en orden ascendente)
12
15
19
28
29
30
30
30
30
30
30
30
30
32
33
34
35
35
35
36
36
36
37
37
37
37
38
38
38
38
39
39
39
39
39
40
40
40
41
41
42
42
42
42
42
43
43
46
46
51

En este caso, la posición de la mediana es P = 0.5 * (50 + 1) = 25.5, entonces ${{P}_{L}}=25$ y ${{P}_{U}}=26$. El valor en la posición 25 ^th en los datos en orden ascendente es 37, y el valor en la posición 26 también es 37. La mediana es entonces

\[Median=\frac{{37}+{37}}{2}=37\]

La moda, que es el valor más repetido, es 30.

¿Qué es más grande, la media, la mediana o la moda?

Esa es una pregunta que surge con frecuencia. En términos generales, no hay una respuesta para todas las distribuciones. Es decir, la respuesta depende de la distribución.

Para una distribución simétrica tenemos :

\[\Large \text{Mode} = \text{Median} = \text{Mean} \]

Gráficamente:

Media, mediana y moda para una distribución simétrica

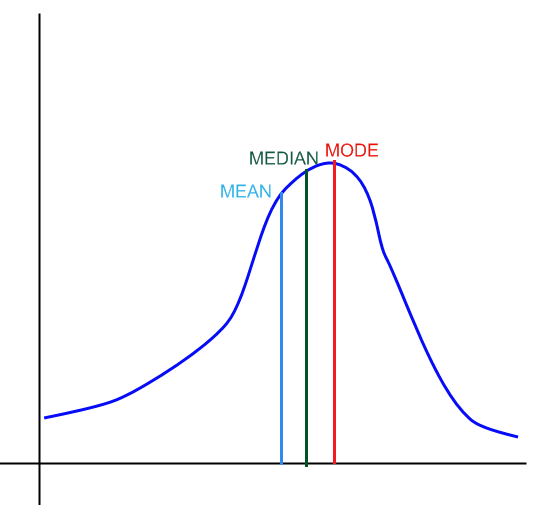
Para una distribución sesgada a la derecha tenemos :

\[\Large \text{Mode} \le \text{Median} \le \text{Mean} \]

Gráficamente:

Para una distribución sesgada a la izquierda tenemos :

\[\Large \text{Mean} \le \text{Median} \le \text{Mode} \]

Gráficamente:

Mediana, media y moda para una distribución sesgada a la izquierda

Más sobre la media, la mediana y la moda

La mediana, la media y la moda son conceptos ampliamente populares que se utilizan en todas las partes en Estadística. Representan medidas de centro, que intentan dar un valor que sea representativo de la muestra.

Dependiendo del nivel de medición, usaríamos una medida de centro diferente.

• Para datos nominales, usamos el modo.

• Para datos ordinales, no cuantitativos, utilizamos la moda y la medida del centro.

• Para datos cuantitativos ordinales, usamos la mediana o la media como medida del centro.

• Para los datos de intervalo y razón, usamos la media (o la mediana si la distribución es demasiado sesgada) como medida del centro.

Aplicaciones

La media, la mediana y la moda son las medidas de centro más utilizadas. La media y la mediana se utilizan para datos cuantitativos y la moda se utiliza para datos categóricos.

Para datos cuantitativos, normalmente se usaría la media. Con una salvedad: la media es muy sensible a los valores atípicos. Esto significa que un valor atípico (ya sea un valor legítimo o un error de escritura) podría marcar una diferencia drástica en el valor de la media.

En tales casos, cuando hay valores atípicos o la distribución está bastante sesgada, es preferible utilizar la mediana como la medida más precisa del centro, ya que la media se distorsiona por el sesgo o los valores atípicos.

Un ejemplo de esto es cuando se recolectan muestras para evaluar los ingresos de los encuestados. Si tomamos una muestra de 100 personas y encontramos que 99 de ellas ganan $ 10,000 por año, y 1 persona gana $ 100 millones por año, el ingreso promedio de esa muestra sería (10,000 * 99 + 1 * 100,000,000) / 100 = $ 1,009,900.00 . Entonces, en promedio, todo el mundo gana $ 1,009,900.00, por lo que debería la idea de que esta muestra debe provenir de un área muy rica, pero ese no es el caso: es solo un valor atípico que distorsiona mucho la media. De hecho, en este caso, la mediana es $ 10,000, que es un valor de centro mucho más representativo para esta muestra.

Calculadoras relacionadas

Si necesita ver soluciones paso a paso para el cálculo de la media y otras medidas de tendencia central, consulte calculadora de estadística descriptiva . También puede encontrar útiles nuestros Calculadora de resumen de 5 números .