Diagrama de caja y bigotes
El diagrama de caja y bigotes, o también conocido como diagrama de caja, es un tipo de representación gráfica de una muestra, que proporciona características clave fáciles de ver de la distribución de una muestra.
Un diagrama de caja y bigotes proporciona la mediana, así como el primer y tercer cuartiles en su "caja", y el mínimo y máximo en el "bigote".
Cuando los mínimos o máximos son demasiado extremos, los "recortamos" el bigote y anotamos la existencia de un outlier.
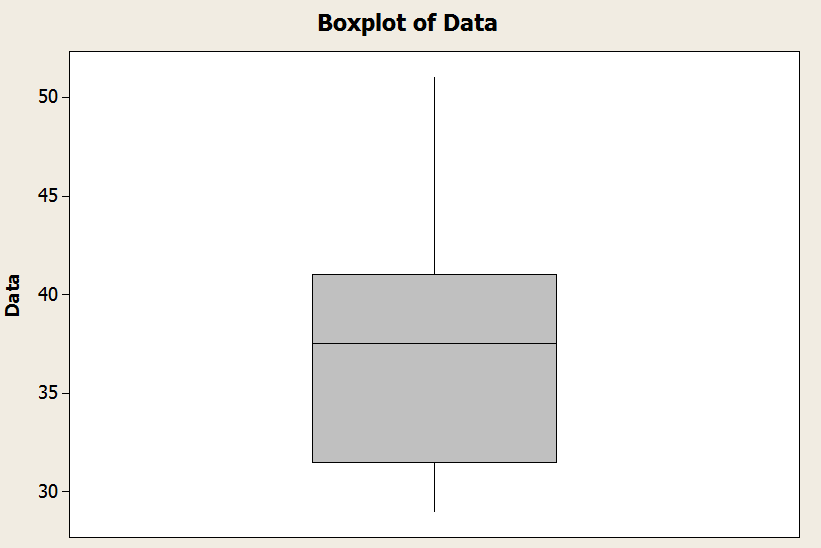
En el gráfico de arriba tienes un ejemplo de cómo se ve un diagrama de caja: Tienes la "caja" y los bigotes.
La línea inferior del cuadro está definida por el primer cuartil (\(Q_1\)).
La línea media del cuadro está definida por la mediana (\(Q_2\)).
La línea superior del cuadro está definida por el tercer cuartil (\(Q_3\)).
Ahora bien, para los bigotes hay una regla a seguir: el bigote inferior se define por el mínimo de la muestra y el bigote superior se define por el máximo de la muestra. Esto siempre que el tamaño del bigote sea menor que \(1.5 \times IQR\), donde \(IQR\) es el rango intercuartil, y está definido por \(IQR = Q_3 - Q_1\).
Vea el gráfico de muestra a continuación.
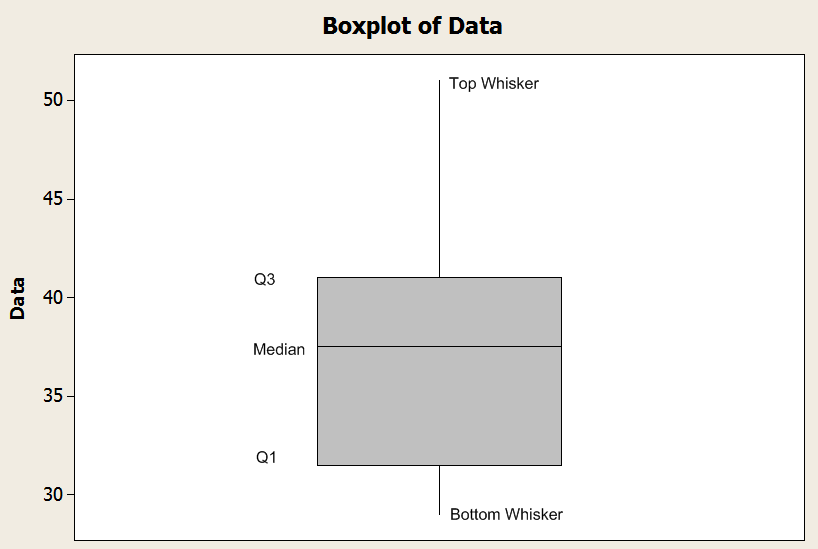
Entonces, si el mínimo de la muestra es mayor que \(Q_1 - 1.5 \times IQR\), entonces el bigote inferior está definido por el mínimo. De lo contrario, está definido por \(Q_1 - 1.5 \times IQR\).
De manera similar, si el máximo de la muestra es menor que \(Q_3 + 1.5 \times IQR\), entonces el bigote superior se define por el máximo. De lo contrario, está definido por \(Q_3 + 1.5 \times IQR\).
EJEMPLO 1
Construya un diagrama de caja para la siguiente muestra:
28, 36, 43, 30, 46, 19, 46, 36, 34, 38, 42, 29, 37, 35, 39, 39, 30, 39, 36, 38, 30, 41, 42, 46, 40, 33, 30, 40, 43, 30, 42, 39, 30, 35, 38, 41, 30, 37, 40, 30, 30, 35, 39, 37, 42, 42, 37, 38, 32, 51
RESPONDER:
Conseguimos que el máximo y el mínimo son
\[\min = 19\] \[\max = 51\]La siguiente tabla muestra los datos en orden ascendente:
|
Datos (en orden ascendente) |
|
19 |
|
28 |
|
29 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
32 |
|
33 |
|
34 |
|
35 |
|
35 |
|
35 |
|
36 |
|
36 |
|
36 |
|
37 |
|
37 |
|
37 |
|
37 |
|
38 |
|
38 |
|
38 |
|
38 |
|
39 |
|
39 |
|
39 |
|
39 |
|
39 |
|
40 |
|
40 |
|
40 |
|
41 |
|
41 |
|
42 |
|
42 |
|
42 |
|
42 |
|
42 |
|
43 |
|
43 |
|
46 |
|
46 |
|
46 |
|
51 |
La mediana es entonces
\[Median=\frac{{37}+{38}}{2}=37.5\]La posición del percentil 25 es
\[{{L}_{25}}=\frac{P}{100}\times \left( n+1 \right)=\frac{25}{100}\times \left( 50+1 \right) = {12.75}\]Entonces, obtenemos eso
\[{{Q}_{1}}={30} +{0.75}\times \left( {32}-{30} \right) = {31.5}\]La posición del percentil 75 es
\[{{L}_{75}}=\frac{P}{100}\times \left( n+1 \right)=\frac{75}{100}\times \left( 50+1 \right) = {38.25}\]Entonces, obtenemos eso
\[{{Q}_{3}}={41}+{0.25}\times \left( {41}-{41} \right) = {41}\]Por lo tanto, el resumen de 5 números es
\[\min = 19, Q_1 = 31.5, Q_2 = 37.5, Q_3 = 41, \max = 51\]El rango intercuartílico en este caso es \(IQR = Q_3 - Q_1 = 41 - 31.5 = 9.5\). Por lo tanto,
\(Q_1 - 1.5 \times IQR = 31.5 - 1.5 \times 9.5 = 17.25\)
\(Q_3 + 1.5 \times IQR = 41 + 1.5 \times 9.5 = 55.25\)
Observe que el mínimo es 19 y es mayor que \(Q_1 - 1.5 \times IQR = 17.25\). Y el máximo es 51, y es menor que \(Q_3 + 1.5 \times IQR = 55.25\).
Concluimos que el bigote inferior es el mínimo y el bigote superior es el máximo en este caso. Gráficamente
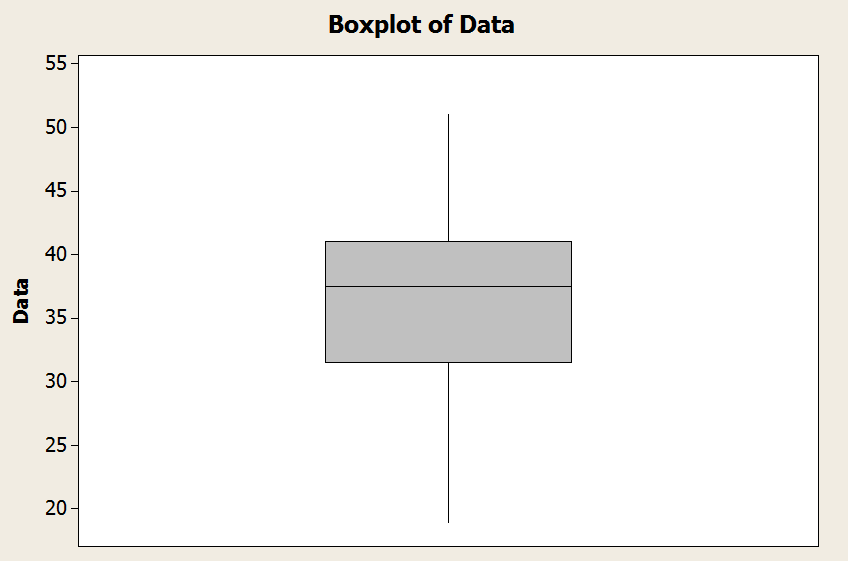
EJEMPLO 2
Encuentre el diagrama de caja para la misma muestra del ejemplo anterior, pero cuando reemplace "51" por "81".
RESPONDER:
Conseguimos que el máximo y el mínimo son
\[\min = 19\] \[\max = 81\]La siguiente tabla muestra los datos en orden ascendente:
|
Datos (en orden ascendente) |
|
19 |
|
28 |
|
29 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
32 |
|
33 |
|
34 |
|
35 |
|
35 |
|
35 |
|
36 |
|
36 |
|
36 |
|
37 |
|
37 |
|
37 |
|
37 |
|
38 |
|
38 |
|
38 |
|
38 |
|
39 |
|
39 |
|
39 |
|
39 |
|
39 |
|
40 |
|
40 |
|
40 |
|
41 |
|
41 |
|
42 |
|
42 |
|
42 |
|
42 |
|
42 |
|
43 |
|
43 |
|
46 |
|
46 |
|
46 |
|
81 |
La mediana es entonces
\[Median=\frac{{37}+{38}}{2}=37.5\]La posición del percentil 25 es
\[{{L}_{25}}=\frac{P}{100}\times \left( n+1 \right)=\frac{25}{100}\times \left( 50+1 \right) = {12.75}\]Entonces, obtenemos eso
\[{{Q}_{1}}={30} +{0.75}\times \left( {32}-{30} \right) = {31.5}\]La posición del percentil 75 es
\[{{L}_{75}}=\frac{P}{100}\times \left( n+1 \right)=\frac{75}{100}\times \left( 50+1 \right) = {38.25}\]Entonces, obtenemos eso
\[{{Q}_{3}}={41}+{0.25}\times \left( {41}-{41} \right) = {41}\]Por lo tanto, el resumen de 5 números es
\[\min = 19, Q_1 = 31.5, Q_2 = 37.5, Q_3 = 41, \max = 81\]El rango intercuartílico en este caso es \(IQR = Q_3 - Q_1 = 41 - 31.5 = 9.5\). Por lo tanto,
\(Q_1 - 1.5 \times IQR = 31.5 - 1.5 \times 9.5 = 17.25\)
\(Q_3 + 1.5 \times IQR = 41 + 1.5 \times 9.5 = 55.25\)
Observe que el mínimo es 19 y es mayor que \(Q_1 - 1.5 \times IQR = 17.25\). Pero ahora el máximo es 81, que supera \(Q_3 + 1.5 \times IQR = 55.25\). Por lo tanto, el valor "81" es un valor atípico.
Concluimos que el bigote inferior es el mínimo y el bigote superior está definido por \(Q_3 + 1.5 \times IQR = 55.25\). Gráficamente
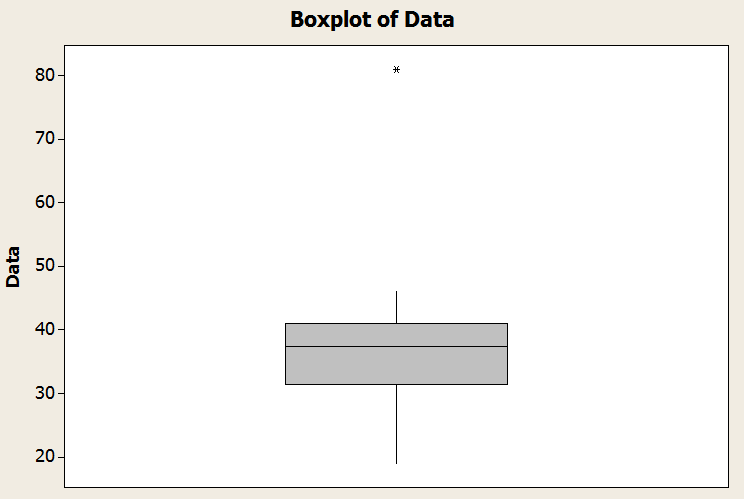
Más sobre el diagrama de caja
La pregunta principal que tiene la gente es qué te dicen los diagramas de caja. Qué representan. Y la respuesta es simple: le brindan una descripción resumida de la distribución de una muestra al proporcionar un gráfico esquemático que muestra la posición relativa del Resumen de 5 números .
De esta manera, puede buscar valores atípicos , puede evaluar el grado de asimetría de la distribución y puede escanear rápidamente las regiones que tienen el 25%, 50% y 75% de la distribución total.
Diferencia entre diagrama de caja e histograma
Una de las cosas sobre el diagrama de caja es que proporciona información que es ligeramente diferente a la información proporcionada por un histograma.
De hecho, el histograma muestra la forma bruta de la distribución, basada en las clases utilizadas para clasificar los posibles valores de la variable aleatoria. Por otro lado, la gráfica de caja proporciona información resumida sobre los cuartiles y el resumen de 5 números, lo que le dice mucho sobre la posición relativa del primer y tercer cuartil con respecto a la mediana.
En otras palabras, el diagrama de caja, a diferencia del histograma, presenta un gráfico que representa un resumen de la distribución , en lugar de una descripción cruda. Los únicos valores brutos que irían en un diagrama de caja serían los valores atípicos (si los hubiera).
Aplicaciones
La aplicación más clásica del diagrama de caja es la detección de valores atípicos. Por definición, el diagrama de caja limita el tamaño de los bigotes a 1,5 veces el rango intercuartílico \((IQR)\) desde los extremos de la caja (que están definidos por \(Q_1\) y \(Q_3\).
Entonces, entonces, cualquier punto que vaya más allá del tamaño máximo de los bigotes se anotará en el diagrama de caja y se considerará un valor atípico.
Practique los conceptos que ha aprendido en este tutorial utilizando este fabricante de diagramas de caja . Otro creador de gráficos que permitirá ver de un vistazo las propiedades distributivas de la distribución de una muestra es este creador de histogramas , o esto plotter de tallo y hojas .