Desigualdades de valor absoluto
Las desigualdades de valor absoluto son desigualdades en las que hay una o más valor absoluto . Recordemos que una desigualdad es casi como una ecuación, pero en lugar del signo "=", tenemos "≤" o "≥".
Esta diferencia hace que el conjunto de soluciones sea típicamente una región, como ocurre con la mayoría de las desigualdades. Y el hecho de que intervengan valores absolutos indica un cierto tratamiento especial para su resolución.
En este tutorial nos concentraremos en las habilidades específicas requeridas para la resolución de este tipo de desigualdad que contiene uno o más valores absolutos. Además, asumiremos que una o dos variables, \(x\) y / o \(y\) están involucradas en la desigualdad.
¿Qué es una desigualdad de valor absoluto?
Para el propósito de este análisis, consideraremos una desigualdad de valor absoluto como una desigualdad que involucra una o dos variables, con al menos un valor absoluto.
Por ejemplo, a continuación tenemos una desigualdad de valor absoluto con dos variables \(x\) y \(y\):
\[|3x+2y-1| \ge 1\]O también, podríamos tener la siguiente desigualdad de valor absoluto con una sola variable:
\[|3x-1| \le 2\]Para nuestros propósitos, y para el propósito de las técnicas utilizadas para su resolución, trataremos ambos tipos de desigualdades (una y dos variables)
¿Cómo resolver las desigualdades de valor absoluto?
Al resolver ecuaciones o desigualdades, no existe realmente una fórmula mágica que resuelva todo. Cada problema es diferente y puede tener sus propias peculiaridades.
Lo mejor que podemos hacer es proporcionar una serie de pasos que le ayudarán en el proceso de resolver una desigualdad.
Paso 1:
Para cada absoluto, determine las regiones en las que el argumento del valor absoluto es negativo y en las que no es negativo.
Paso 2:
Si solo hay un valor absoluto en la desigualdad, resuélvalo en ambas áreas (donde el argumento del valor absoluto es negativo y donde no es negativo).
Paso 3:
Si hay más de un valor absoluto en la desigualdad, debe intersecar todas las regiones para obtener un conjunto de particiones más pequeñas. En cada partición, necesita conocer EXACTAMENTE el signo de cada argumento. Luego, resuelve la desigualdad en todas las áreas.
Paso 4:
Una vez que obtenga la solución de la pieza que se encuentra en cada una de las áreas, la solución final es simplemente la unión de estas soluciones de la pieza.
En palabras simples: debe averiguar las regiones en las que conoce exactamente el signo del argumento de los valores absolutos (para que pueda deshacerse de ellos).
Un par de ejemplos deberían aclarar estos pasos.
EJEMPLO 1
Resuelve la siguiente desigualdad
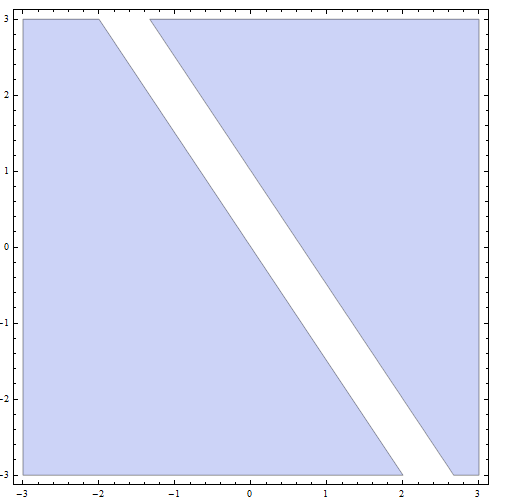
\[| 2x + 4y - 1 | \ge 2\]RESPONDER:
Para resolver la desigualdad, debemos seguir los pasos que se especificaron anteriormente.
Paso 1: Solo hay un valor absoluto, por lo que debemos determinar si el argumento es negativo y no negativo. Por lo tanto, primero debemos resolver:
\[2x + 4y - 1 \ge 0\]Existen varias estrategias para resolver lo anterior, pero la más fácil es resolver primero la ecuación
\[2x + 4y - 1 = 0\]lo que significa que \(4y = -2x + 1\) o lo mismo que \(y = -\frac{1}{2}x + \frac{1}{4}\), que corresponde a una línea con pendiente \(m = -\frac{1}{2}\) e intersección en y \(n = \frac{1}{4}\).
Ahora, para cuidar de \(2x + 4y - 1 \ge 0\) probamos si el punto \((0,0)\) satisface o no la desigualdad:
\[2(0) + 4(0) - 1 = -1 < 0\]Entonces, \((0,0)\) satisface o no la desigualdad. La conclusión es que la recta con pendiente \(m = -\frac{1}{2}\) e intersección con el eje y \(n = \frac{1}{4}\) divide el plano en dos regiones:
Para los puntos debajo de la línea (llamamos a esta región 1, \(R_1\)), obtenemos que \(2x + 4y - 1 < 0\)
Para los puntos por encima de la línea, incluida la línea en sí (llamamos a esta región 2, \(R_2\)) obtenemos que \(2x + 4y - 1 \ge 0\)
¿Porque es esto importante? ¿Por qué nos tomamos todos estos problemas? Porque en \(R_1\), obtenemos eso desde \( 2x + 4y - 1 < 0\), luego \(| 2x + 4y - 1 | = -(2x + 4y - 1) \). De manera similar, en \(R_2\), obtenemos eso desde \( 2x + 4y - 1 \ge 0\), luego \(| 2x + 4y - 1 | = 2x + 4y - 1 \).
Paso 2: Ahora necesitamos resolver la desigualdad en la región 1, \(R_1\) :
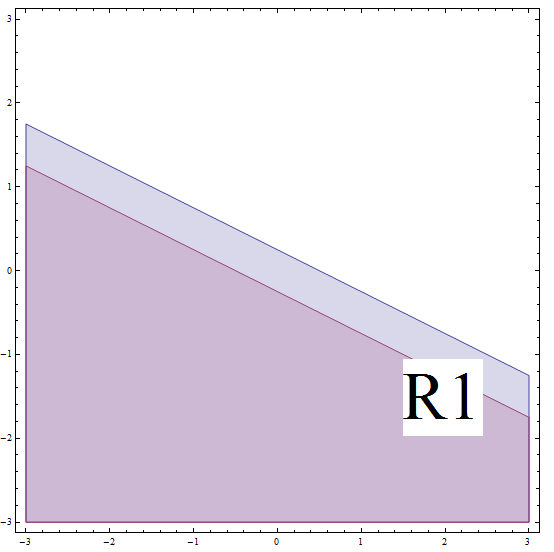
\[| 2x + 4y - 1 | \ge 2\] \[\Rightarrow -(2x + 4y - 1) \ge 2\] \[\Rightarrow 2x + 4y - 1 \le -2 \text{ (multiplying by (-1) changes the direction of the inequality)}\] \[\Rightarrow 2x + 4y \le -1\] \[\Rightarrow 4y \le -2x - 1\] \[\Rightarrow y \le -\frac{1}{2}x - \frac{1}{4} \]Esto corresponde a todos los puntos debajo o en la línea con pendiente \(m = -\frac{1}{2}\) e intersección y \(n = -\frac{1}{4}\). Pero no olvide que está en \(R_1\), y esta línea que encontramos está DEBAJO del límite de \(R_1\) (vea el gráfico a continuación).
Para aclarar, dado que asumimos que estamos en \(R_1\), necesitamos tener que estamos DEBAJO de la línea con pendiente \(m = -\frac{1}{2}\) e intersección en y \(n = \frac{1}{4}\). Bajo este supuesto, resolvimos la desigualdad original y también necesitamos estar debajo de la línea con pendiente \(m = -\frac{1}{2}\) e intersección en y \(n = -\frac{1}{4}\). Estas dos condiciones deben ocurrir simultáneamente, por lo que obtenemos la intersección de las dos regiones.
Entonces, la solución de la pieza en este caso corresponde a todos los puntos debajo o en la línea con pendiente \(m = -\frac{1}{2}\) e intersección y \(n = -\frac{1}{4}\).
Ahora necesitamos resolver la desigualdad en la región 2, \(R_2\) :
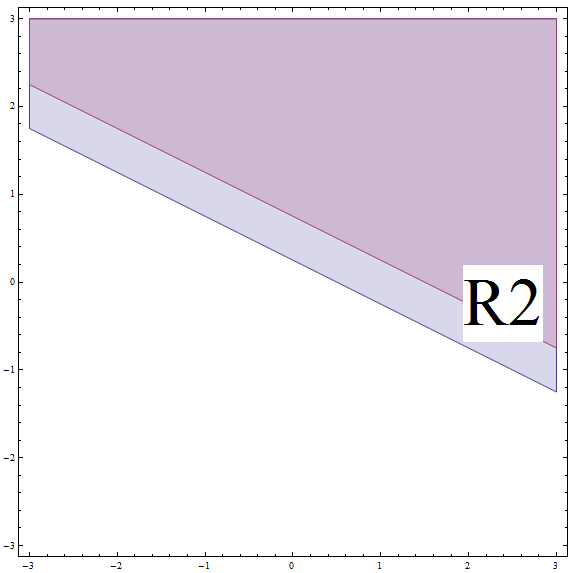
\[| 2x + 4y - 1 | \ge 2\] \[\Rightarrow 2x + 4y - 1 \ge 2\] \[\Rightarrow 2x + 4y \ge 3\] \[\Rightarrow 4y \ge -2x + 3\] \[\Rightarrow y \ge -\frac{1}{2}x + \frac{3}{4} \]Esto corresponde a todos los puntos arriba o en la línea con pendiente \(m = -\frac{1}{2}\) e intersección con el eje y \(n = \frac{3}{4}\). Pero no olvide que está en \(R_2\), y esta línea está POR ENCIMA del límite de\(R_2\) (consulte el gráfico a continuación).
Al encontrar la intersección entre \(R_2\) y la región de arriba, obtenemos que la solución de la parte en este caso son todos los puntos de arriba o en la línea con pendiente \(m = -\frac{1}{2}\) e intersección en y \(n = \frac{3}{4}\).
Paso 4: Ahora, la solución final es la unión de todas las soluciones de las partes de las partes anteriores: La solución final son todos los puntos ABAJO o en la línea con pendiente \(m = -\frac{1}{2}\) e intersección en y \(n = -\frac{1}{4}\), MÁS todos los puntos ARRIBA o en la línea con pendiente \(m = -\frac{1}{2}\) e intersección con el eje y \(n = \frac{3}{4}\).
Gráficamente, obtenemos
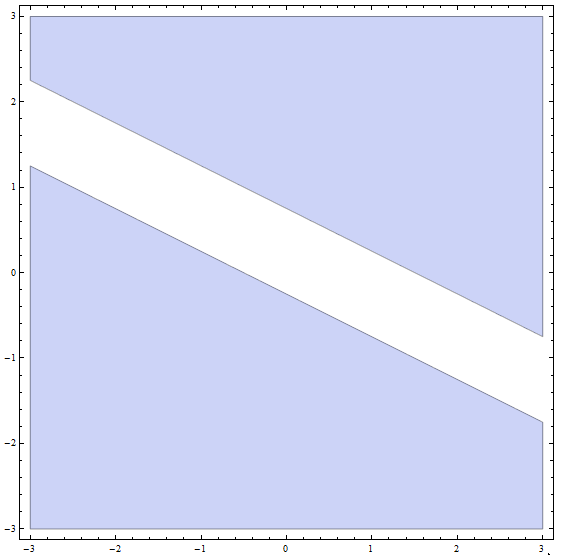
que concluye la resolución de la desigualdad.
EJEMPLO 2
Resuelve la siguiente desigualdad de doble valor absoluto
\[| 2x - 1 | \ge |x + 3|\]RESPONDER:
Esta es una desigualdad de valor absoluto doble porque hay 2 valores absolutos. Esto significa que encontrar las regiones requerirá un poco más de trabajo (relativamente hablando).
Paso 1: Para el primer valor absoluto resolvemos:
\[2x- 1 \ge 0\] \[\Rightarrow \,\, 2x \ge 1\] \[\Rightarrow \,\, x \ge \frac{1}{2}\]Así que obtenemos \(2x- 1 \ge 0\) en \([\frac{1}{2}, +\infty)\) y \(2x- 1 < 0\) en \((-\infty, \frac{1}{2})\).
Para el segundo valor absoluto resolvemos:
\[x+3 \ge 0\] \[\Rightarrow \,\, x \ge -3\]Así que obtenemos \(x+3 \ge 0\) en \([-3, +\infty)\) y \(x+3 < 0\) en \((-\infty, -3)\).
Entonces, definimos 4 regiones:
\(R_1 = [\frac{1}{2}, +\infty) \cap [-3, +\infty) = [\frac{1}{2}, +\infty)\). En esta región obtenemos: \(2x- 1 \ge 0\) AND \(x+3 \ge 0\).
\(R_2 = [\frac{1}{2}, +\infty) \cap (-\infty, -3) = \varnothing\). En esta región obtenemos: \(2x- 1 \ge 0\) AND \(x+3 < 0\), aunque esta región está vacía.
\(R_3 = (-\infty, \frac{1}{2}) \cap [-3, +\infty) = [-3, \frac{1}{2})\). En esta región obtenemos: \(2x- 1 < 0\) AND \(x+3 \ge 0\)
\(R_4 = (-\infty, \frac{1}{2}) \cap (-\infty, -3) = (-\infty, -3)\). En esta región obtenemos: \(2x- 1 < 0\) AND \(x+3 < 0\).
Paso 2: Ahora necesitamos resolver la desigualdad de valor absoluto doble en cada una de las cuatro regiones:
• El \(R_1\):
Aquí obtenemos \(2x- 1 \ge 0\) Y \(x+3 \ge 0\) entonces
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, 2x - 1 \ge x + 3\] \[\Rightarrow \,\, 2x - x \ge 3 - (-1)\] \[\Rightarrow \,\, x \ge 4\]Entonces, para obtener la solución de la pieza, debemos intersecar \(x \ge 4\), o \([4, +\infty)\) con \(R_1\).
Por lo tanto, la solución de la pieza correspondiente es: \([\frac{1}{2}, +\infty) \cap [4, +\infty) = [4, +\infty)\)
• El \(R_2\):
La solución de esta pieza está vacía (\(\varnothing\)).
• El \(R_3\):
Aquí obtenemos \(2x- 1 < 0\) Y \(x+3 \ge 0\) entonces
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x - 1) \ge x + 3\] \[\Rightarrow \,\, 2x - 1 \le -x - 3\] \[\Rightarrow \,\, 2x - (-x) \le -3 - (-1)\] \[\Rightarrow \,\, 3x \le -2\] \[\Rightarrow \,\, x \le -\frac{2}{3}\]Entonces, para obtener la solución de esta pieza, debemos intersecar \( x \le -\frac{2}{3}\), o \( (-\infty, -\frac{2}{3}]\) con \(R_3\).
Por lo tanto, la solución de la pieza correspondiente es: \((-\infty, -\frac{2}{3}] \cap [-3, \frac{1}{2}) = [-3, -\frac{2}{3}] \)
• El \(R_4\):
Aquí obtenemos \(2x- 1 < 0\) Y \(x+3 < 0\) entonces
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x - 1) \ge -(x + 3)\] \[\Rightarrow \,\, 2x - 1 \le x + 3\] \[\Rightarrow \,\, 2x - x \le 3 - (-1)\] \[\Rightarrow \,\, x \le 4\]Entonces, para obtener la solución de esta pieza, debemos intersecar \( x \le 4 \), o \((-\infty, 4]\) con \(R_4\).
Por lo tanto, la solución de la pieza correspondiente es: \((-\infty, -3) \cap (-\infty, 4] = (-\infty, -3) \)
Paso 4:
Finalmente, obtenemos la unión de las soluciones parciales, para obtener que la solución de la desigualdad inicial dada es
Nadie dijo que sería corto, ¿verdad? Bien. No es realmente difícil, solo tienes que ser sistemático y ceñirte al plan.
Más sobre desigualdades con valor absoluto
¿Por qué nos preocupamos por este tipo de desigualdades? Nos importa porque tienen aplicaciones en la práctica.
Por ejemplo, en geometría, las distancias en la línea real deben representarse como un valor absoluto, porque debe ser no negativo.
Se podría tener una determinada situación geométrica en la que es necesario encontrar todos los puntos de la recta real que estén al menos a una distancia de 2 del punto 3. Tal situación se puede describir con la siguiente desigualdad:
\[| x-3 |\ge 2\]Entendamos la desigualdad anterior. El punto \(x\) es el punto en el que queremos satisfacer la desigualdad. La distancia desde \(x\) al punto 3 está representada por \(|x - 3|\).
Luego, estamos tratando de encontrar los puntos que están al menos a una distancia de 2 del punto 3, por lo que la distancia \(|x - 3|\) debe ser de al menos 2, lo que explica \(|x - 3| \ge 2.\)
Este es solo un tipo de problemas de desigualdad de valor absoluto que puede encontrar en la práctica.
¿Puedes encontrar desigualdades en valor absoluto sin solución?
Usted apuesta. Aquí tienes uno \(|2x| < |x|\). Es posible que una desigualdad sea simplemente inviable como el caso de este que les acabo de dar.
¿Qué tal graficar desigualdades en valor absoluto?
El proceso de graficarlos es importante de la mano con el proceso de resolverlos: necesitas encontrar las regiones donde sabes exactamente si los argumentos de los valores absolutos son positivos o negativos, y luego las desigualdades de valor absoluto se encuentran en desigualdades simples, que está trivialmente graficado. Luego, simplemente se unen todas las piezas de las regiones obtenidas.