Eliminación gaussiana
La eliminación gaussiana es un proceso realizado en matrices cuyo objetivo es poner una matriz en forma escalonada . Tener una matriz en tal forma ayuda enormemente a resolver ecuaciones matriciales con mucha facilidad.
Técnicamente, el proceso de realizar la eliminación gaussiana consiste en encontrar una columna con un pivote (que es el argot elegante para un elemento distinto de cero) que nos permite eliminar todos los elementos debajo del pivote.
Este proceso de encontrar pivotes y eliminar nos permite poner una matriz en forma escalonada, y la forma en que avanza el proceso es tal que al girar, agrega una nueva columna a la forma escalonada, y no 'arruina' la forma escalonada. ha hecho hasta el paso anterior. Hermoso si me preguntas.
El término "forma escalonada" que se obtiene mediante el uso de la eliminación gaussiana se aclara al observar la matriz anterior, donde los elementos distintos de cero de la matriz tienen esta estructura escalonada, como se muestra en la línea roja.
La matemática detrás del pivote y la eliminación gaussiana
No nos vamos a poner demasiado técnicos en esto, solo vamos a intentar que entiendas la motivación y la mecánica de este tipo de eliminación.
La idea es obtener una matriz \(A\), de dimensión \(m \times n\) (esto es, tiene \(m\) filas y \(n\) columnas) en una forma diferente que sea más adecuada para resolver ecuaciones.
Más específicamente, para una matriz \(m\times n\) \(A\), y un vector \(m\times 1\) \(b\), necesitamos encontrar un vector \(n\times 1\) \(x\) tal que
\[Ax = b\]Puedes pensar, "eso es tan fácil, simplemente multiplicamos cada lado por \(A^{-1}\) de la izquierda", por lo que obtenemos:
\[x = A^{-1} b \]....¡No tan rapido! Eso solo funciona cuando la matriz \(A\) es invertible. Para empezar, la matriz \(A\) tiene que ser una matriz cuadrada, y luego, su determinante debe ser diferente de cero. Pero no se puede multiplicar por la inversa para matrices no cuadradas. Entonces, ¿cómo lo haces entonces?
Necesitas TRANSFORMAR la ecuación en una que sea más fácil de resolver.
Específicamente, las matrices en forma escalonada son matrices que conducen a ecuaciones que son fáciles de resolver (más sobre esto más adelante).
Usando matrices elementales
En primer lugar, haremos una nota crucial. Si tenemos una solución de la ecuación matricial \(Ax = b\), y \(E\) es una matriz invertible, entonces \(x\) también es una solución de \((EA)x = Eb\), y viceversa.
En otras palabras, las ecuaciones matriciales
\[Ax = b\]y
\[(EA)x = Eb\]son equivalentes, para una matriz invertible \(E\). ¿Qué queremos decir con que las ecuaciones son equivalentes? Queremos decir que las ecuaciones tienen las mismas soluciones.
Entonces, lo que vamos a hacer es comenzar con \(Ax = b\), y multiplicando por matrices invertibles \(E\), vamos a llegar a una ecuación matricial equivalente que es mucho más fácil de resolver .
Digamos que podemos encontrar una lista de matrices invertibles \(E_1, E_2, ..., E_n\) y multiplicamos (desde la izquierda) la ecuación matricial original para transformarla en una ecuación equivalente, como:
\[Ax = b \,\,\,\, \Leftrightarrow \,\,\,\, (E_1 \cdot A)x = (E_1 \cdot b)\] \[... \Leftrightarrow \,\,\,\, (E_n \cdots E_2 \cdot E_1 \cdot A)x = (E_n \cdots E_2 \cdot E_1 \cdot b)\] \[ \Leftrightarrow \,\,\,\, \tilde A x = \tilde b\]donde \(E_n \cdots E_2 \cdot E_1 \cdot A = \tilde A\) y \(E_n \cdots E_2 \cdot E_1 \cdot A = \tilde b\).
Nuestro objetivo es cuidadosamente escoger las matrices invertibles \(E_1, E_2, ..., E_n\) de modo que \(\tilde A\) está en forma escalonada.
¿Porqué es eso? Porque si \(\tilde A\) está en forma escalonada, resolver la ecuación matricial \(\tilde A x = \tilde b\) es mucho más fácil, y ya sabemos que \(\tilde A x = \tilde b\) tiene las mismas soluciones que \(A x = b\)
EJEMPLO 1
Veamos por qué es mucho más fácil resolver una ecuación matricial cuando la tienes en forma escalonada. Primero imagina que tienes la siguiente matriz y vector:
\[A= \left[ \begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ -1 & 1 & -1 \\ \end{matrix} \right]\] \[b= \left[ \begin{matrix} 2 \\ 1 \\ 1 \\ \end{matrix} \right]\]y quieres resolver \(Ax = b\). ¿Cómo se vería el sistema de ecuaciones? El sistema \(Ax = b\) se vería así
\[x_1 + x_2 + x_3 = 2\] \[x_1 - x_2 + x_3 = 1\] \[-x_1 + x_2 - x_3 = 1\]¿Cómo se ve? Bueno, no tan ordenado. Necesitarías empezar a hacer malabares con las ecuaciones. Hay enfoques más o menos sistemáticos para resolver esto utilizando cosas como eliminación y demás, pero al menos es engorroso.
Ahora, por otro lado, imagina que tienes la siguiente matriz y vector:
\[\tilde A = \left[ \begin{matrix} -1 & 1 & 1 \\ 0 & 1 & -1 \\ 0 & 0 & 1 \\ \end{matrix} \right] \] \[\tilde b= \left[ \begin{matrix} 1 \\ -1 \\ -1 \\ \end{matrix} \right]\]y quieres resolver \(\tilde A x = \tilde b\). En este caso, la matriz \(\tilde A\) está en forma escalonada. ¿Cómo se vería el sistema de ecuaciones? El sistema \(\tilde A x = \tilde b\) se vería así
\[-x_1 + x_2 + x_3 = 1\] \[x_2 - x_3 = -1\] \[x_3 = -1\]¿Cómo se ve este? Bueno, no está mal.
De hecho, si partimos directamente de la tercera ecuación, tenemos ese \(x_3 = -1\) directamente. Luego, de la segunda ecuación, \(x_2 = -1 + x_3 = -1 + (-1) = -2\). Y de la primera ecuación, \(x_1 = x_2 + x_3 -1 = -2 + (-1) - 1 = -4\). Entonces, sin ningún problema, hemos encontrado que:
\[x_1 = -4, \, x_2 = -2, x_3 = -1\]Por tanto, en este caso el sistema se resuelve de forma trivial.
Para los sistemas asociados a matrices en forma escalonada, es sencillo retroceder de la última ecuación a la primera ecuación para obtener las soluciones.
Cómo elegir las matrices invertibles adecuadas
Ahora que sabemos que trabajar con matrices en forma escalonada hace que sea mucho más fácil resolver ecuaciones matriciales, deberíamos preguntarnos cuáles son las matrices invertibles \(E_1, E_2, ..., E_n\) que harán \(\tilde A\) en forma escalonada.
¿Cómo funciona la eliminación gaussiana?
Curiosamente, no es difícil encontrar estas matrices \(E_1, E_2, ..., E_n\), que se llamarán matrices elementales.
Paso 1
: Mire la primera columna, si tiene un valor distinto de cero, ese será su pivote. Si la primera fila de la primera columna no es cero, úsela como pivote. Si no es así, busque una fila que tenga un valor distinto de cero y permute esa fila y la primera fila.
Entonces, encuentra un pivote y, potencialmente, necesita hacer una permutación de fila (que en realidad se representa multiplicando por una cierta matriz invertible)
Paso 2
: Una vez que tenga un pivote, elimine todos los elementos de la columna actual, debajo del pivote.
Esto se hace multiplicando la fila de pivote por una cierta constante y agregándola a una fila debajo del pivote, de modo que el elemento en la misma columna que el pivote se haga cero.
Paso 3
: Una vez que todos los elementos debajo del pivote se hayan convertido en cero al realizar las operaciones de fila apropiadas (que están representadas por la operación de una matriz invertible), muévase a la siguiente columna, a la siguiente fila, y busque un pivote de la fila de abajo de la fila del pivote anterior y realizar el mismo procedimiento.
Paso 4
: Repita hasta que se quede sin columnas o la matriz esté en forma escalonada.
EJEMPLO 2
Utilizando la eliminación pivotante y gaussiana, resuelva el siguiente sistema:
\[x_1 + x_2 + x_3 = 2\] \[x_1 - x_2 + x_3 = 1\] \[-x_1 + x_2 + x_3 = 1\]RESPONDER:
En primer lugar, la matriz asociada \(A\) y el vector \(b\) son:
\[A= \left[ \begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ -1 & 1 & 1 \\ \end{matrix} \right]\] \[b= \left[ \begin{matrix} 2 \\ 1 \\ 1 \\ \end{matrix} \right]\]La matriz aumentada \([A|b]\) es
\[\left[ \begin{matrix} 1 & 1 & 1 & 2 \\ 1 & -1 & 1 & 1 \\ -1 & 1 & 1 & 1 \\ \end{matrix} \right]\]Para resolver el sistema, necesitamos ir a la eliminación gaussiana. Elegimos el primer pivote, comenzando por la primera columna. El elemento en la primera fila de la primera columna es 1, que es diferente de cero y luego se usa como pivote. Usamos ese pivote (1) para eliminar todos los elementos debajo de él:
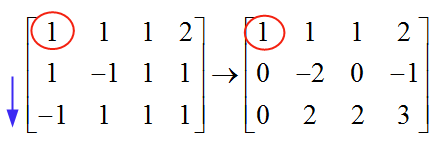
La mecánica de eliminar los elementos debajo del pivote es simple. En este caso, para eliminar el "1" que está debajo del pivote, resto los elementos de la fila 1 a los elementos de la fila 2. De esa manera formo un cero debajo del pivote.
De manera similar, para eliminar el "-1" que está en la fila 3, agrego los elementos de la fila 1 a los elementos de la fila 3. De esa manera formo un cero debajo del pivote en la fila 3.
Veremos que estas operaciones de fila se logran multiplicando por matriz invertible, por lo que tenemos sistemas equivalentes al hacerlo.
Ahora, moviéndonos a la siguiente fila, a la siguiente columna, encontramos un "-2", que es diferente de cero y, por lo tanto, se utiliza como pivote. Para eliminar el valor debajo de este pivote, agregamos a la fila 3 los valores de la fila 2:
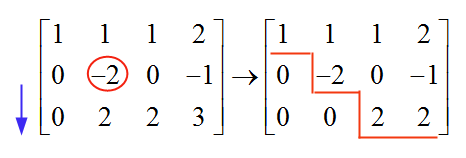
y ahora nos detenemos, porque la matriz resultante ya está en forma escalonada. Ahora retrocedemos para resolver el sistema:
\[2x_3 = 2 \,\,\,\, \Rightarrow \,\,\,\, x_3 = 1\] \[-2x_2 = -1 \,\,\,\, \Rightarrow \,\,\,\, x_2 = 1/2\] \[x_1+x_2+x_3 = 1 \,\,\,\, \Rightarrow \,\,\,\, x_1 = 1 - x_2 - x_3 = 1 - 1/2 - 1 = -1/2\]Más sobre la eliminación gaussiana
Girar y usar la eliminación de pivotes son la base fundamental para resolver sistemas lineales. Pero va más allá de eso. Si solo nos importaran los sistemas lineales, usaríamos Regla de Cramer , que funciona bien para sistemas de resolución .
La eliminación gaussiana tiene la ventaja de que proporciona una forma sistemática de poner matrices en forma escalonada, lo que a su vez conduce a la rápida obtención de ciertas descomposiciones matriciales (LU, LDU, etc.), o incluso al cálculo de la inversa de la matriz .
Matrices elementales de permutación
No hay reglas generales para factorizar expresiones generales. Necesitamos jugar de oído e intentar explotar la estructura de la expresión. A veces podemos factorizar, a veces no. Todo depende de la expresión. La única regla general es tratar de agrupar e intentar encontrar factores comunes para agrupar y simplificar aún más.
Matrices elementales de operaciones de fila
La clave del método de pivote para encontrar soluciones es que las permutaciones y las operaciones de fila son matrices invertibles, por lo que el sistema que estamos transformando en cada paso es equivalente al sistema original.
De hecho, tanto la permutación de filas como las operaciones de fila están representadas por matrices invertibles. Considere la matriz \(E_{ij}\), que se obtiene tomando la matriz identidad \(I\) y permutando sus filas \(i\) y \(j\).
El efecto de multiplicar la matriz \(E_{ij}\) a cualquier matriz \(A\) de la izquierda es obtener las filas \(i\) y \(j\) de \(A\) permutadas.
Ahora considere la matriz \(E_{ij}^{\lambda}\), para \(i < j\), que corresponde a la matriz de identidad para todas las filas, excepto para la fila \(i\), donde el valor de la i th la columna es \(\lambda\) en lugar de 0.
¿Qué hay de las operaciones con columnas?
A veces necesitamos permutar columnas para encontrar un pivote. En ese caso, necesitamos multiplicar la matriz \(E_{ij}\) de la DERECHA, y el resultado será obtener las columnas \(i\) y \(j\) de \(A\) permutadas.