Resumen de cinco números

Más sobre esto Calculadora resumida de 5 números para que comprendas mejor los resultados paso a paso que proporciona esta calculadora.

¿cómo se calcula el resumen de 5 números?

Lo primero que debes saber es cuáles son las partes de un resumen de 5 números, que es una de las técnicas más comunes utilizadas en estadística descriptiva.

El resumen de cinco números es un conjunto de 5 estadísticas descriptivas diferentes que le brindarán una vista rápida y precisa de la distribución de los datos de muestra que está analizando.

Este cálculo es un proceso de varios pasos, que implica obtener 5 datos. De hecho, para un conjunto de muestras de datos, el resumen de cinco números es un conjunto de cinco números que proporcionan una percepción rápida sobre la forma de la distribución. El resumen de cinco números incluye el Mínimo , el primer cuartil \((Q_1)\), la mediana , el tercer cuartil \((Q_3)\) y el máximo .

El Resumen de cinco números puede informarle sobre el centro y la dispersión de la distribución de la muestra, así como el tipo de asimetría (si la hay) y los posibles valores atípicos.

Pasos necesarios para el cálculo del resumen de 5 números

Cómo encontrarlo dependerá de cómo quieras proceder y verás que tienes diferentes formas de calcularlo.

1. Si utiliza nuestra calculadora, todo lo que necesita hacer es proporcionar los datos de muestra y la calculadora realizará el trabajo mostrándole todos los pasos.
2. Si usa Excel, necesitará calcular cada uno de los componentes del resumen de 5 números por separado, ya que no existe una función específica para obtenerlos a la vez. Sin embargo, una pequeña característica de Excel es que tiende a utilizar un método demasiado simplificado para calcular los cuartiles.
3. Si lo hace a mano, necesitará ordenar los datos en orden ascendente. Entonces, el primer número será el mínimo y el último será el máximo. La mediana y los cuartiles se calculan utilizando una convención de interpolación para la posición de los valores en la lista.

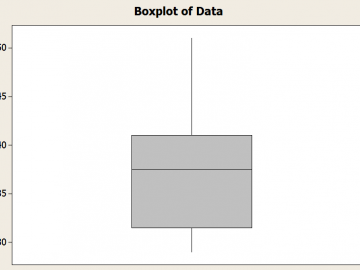
El diagrama de caja resumen de 5 números

¿Cómo son el resumen de los 5 números y el diagrama de caja relacionado ?. Bueno, es una relación muy estrecha, ya que el diagrama de caja se construye esencialmente BASADO en los 5 números.

De hecho, los límites inferior y superior de la caja están dados por el cuartiles Q1 y Q3 , los bigotes están determinados por el máximo y el mínimo (aunque hay un límite basado en el valor del RIQ , utilizando el criterio de RIQ de 1,5 veces)

Calculadoras estadísticas más descriptivas

Por otro lado, es posible que le interese obtener una lista completa de estadísticas descriptivas, que incluye las medidas más comunes de tendencia central y desviación. Para hacerlo, puedes seguir nuestro paso a paso. calculadora de estadísticas descriptivas

. Además, el resumen de 5 números juega un papel crucial en la construcción del diagrama de caja , que le dice mucho sobre la distribución de datos de muestra dados, así como para la detección de valores atípicos .

Resumiendo

El resumen de 5 números es una colección de números que le ayudan a representar medidas de tendencia central y dispersión a partir de algunos datos de muestra determinados. Los componentes son:

• El mínimo
• El primer cuartil
• la mediana
• El tercer cuartil
• el maximo

Ejemplo de resumen de cinco números:

Pregunta : Considere los siguientes datos de muestra: 1, 1, 2, 3, 4, 4, 2, 3, 2, 1, 2, 3, 4, 5, 6, 6, 6, 2, 10, 11. Calcule los cinco -Resumen numérico a mano, mostrando todos los cálculos.

Solución:

Estos son los datos de muestra que se han proporcionado:

Observación	\(X\)
1	1
2	1
3	2
4	3
5	4
6	4
7	2
8	3
9	2
10	1
11	2
12	3
13	4
14	5
15	6
16	6
17	6
18	2
19	10
20	11

Estos son los datos de muestra que se han proporcionado:

Posición	\(X\) (Asc. Order)
1	1
2	1
3	1
4	2
5	2
6	2
7	2
8	2
9	3
10	3
11	3
12	4
13	4
14	4
15	5
16	6
17	6
18	6
19	10
20	11

Según la tabla anterior, el mínimo es \(\min = 1\) y el máximo es \(\max = 11\). Ahora la posición del primer cuartil \(Q_1\) es:

\[ L_{25} = \frac{25}{100} \times (n+1) = 0.25 \times 21 = 5.25 \]

Dado que \( L_{25} = 5.25\) no es un número entero, el primer cuartil \(Q_1\) se calcula interpolando entre los valores ubicados en las posiciones \(5^{th}\) y \(6^{th}\), como se muestra en la siguiente fórmula:

\[ Q_1 = 2 + (5.25 - 5)\times (2 - 2) = 2\]

Como el tamaño de muestra \(n = 20\) es par, tenemos que \((n+1)/2 = (20+1)/2 = 10.5\) no es un valor entero, por lo que la mediana se calcula directamente encontrando el promedio de los valores ubicados en las posiciones \(10^{th}\) y \(11^{th}\), que es:

\[ median = \displaystyle \frac{3 + 3}{2} = 3.5\]

Ahora la posición del tercer cuartil \(Q_3\) es:

\[ L_{75} = \frac{75}{100} \times (n+1) = 0.75 \times 21 = 15.75 \]

Dado que \( L_{75} = 15.75\) no es un número entero, el tercer cuartil \(Q_3\) se calcula interpolando entre los valores ubicados en las posiciones \(15^{th}\) y \(16^{th}\), como se muestra en la siguiente fórmula:

\[ Q_3 = 5 + (15.75 - 15)\times (6 - 5) = 5.75\]

Por lo tanto, según los resultados encontrados anteriormente, obtenemos el siguiente resumen de cinco números:

Minimum =	\(1\)
\(Q_1\) =	\(2\)
Median =	\(3.5\)
\(Q_3\) =	\(5.75\)
Maximum =	\(11\)