Método de sustitución de integración
El método de integración por sustitución o el método de integración por sustitución es una técnica inteligente e intuitiva que se utiliza para resolver integrales, y juega un papel crucial en la tarea de resolver integrales, junto con la integración por partes y descomposición de fracciones parciales método.
La integración puede ser una operación difícil en ocasiones, y solo tenemos algunas herramientas disponibles para continuar.
Naturalmente, el cálculo de la integral indefinida para algunas funciones elementales básicas (como polinomios, potencias, funciones trigonométricas elementales, etc.) es muy simple.
Pero la pregunta es cómo proceder con el cálculo de la integral indefinida (o primitiva) para funciones más complejas o para la combinación algebraica de funciones.
¿¿Estas listo para rockear?? Lo soy, así que sígueme.
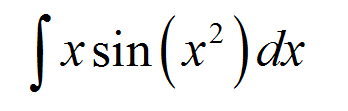
¿Cómo funciona el método de sustitución?
El método de integración por sustitución funciona identificando un "bloque" que contiene la variable de integración, de modo que la derivada de ese bloque también se puede encontrar dentro de la integral. Este método también se denomina comúnmente método de sustitución de u.
Si la estructura de la integral lo permite, este "bloque" se convierte en realidad en una nueva variable de integración, si todo va bien, y la integral se simplifica seriamente.
¿Siempre funciona? No. O dicho de otra manera, siempre puedes hacer una sustitución, pero no siempre la convertirá en una integral más fácil.
¿Por qué intentar este método? Bueno, porque funciona a menudo. Y suele ser el primer truco que debe probar si necesita resolver una integral que no es trivial.
Permítanos poner un par de pasos a seguir si necesita aplicar este método:
PASO 1:
Examine la función que está integrando y busque un "bloque", es decir, una función de \(x\) que aparece una o más veces en la función que está integrando.
PASO 2:
El "bloque" que está buscando debe tener una propiedad muy específica: la derivada del bloque debe aparecer una vez y solo una vez en la función que se está integrando.
PASO 3:
Si los pasos anteriores fueron exitosos, puede usar el "bloque" como la nueva variable, y puede reemplazar la variable y el diferencial por la nueva variable, y la integral que está resolviendo ahora se vuelve mucho más simple.
Nota tecnica : Normalmente trato de que todas las explicaciones sean simples y trato de evitar tecnicismos. En este caso tendré que dar la explicación técnica del método de sustitución, para no dejar las cosas demasiado informales con la idea del "bloque".
Si no le gustan los tecnicismos, puede pasar a la siguiente sección, donde verá los ejemplos.
Entonces, la idea es integrar una función dada \(f(x)\). Entonces necesitamos encontrar:
\[\int f(x) \, dx\]Digamos que la función \(f(x)\) no es una función cualquiera, y tiene una cierta estructura específica, específicamente
\[f(x) = g(h(x))h'(x)\]y suponga que hay una función \(G(x)\) de modo que \(G'(x) = g(x)\) (entonces \(G\) es la antiderivada de \(g\)). Entonces, obtenemos eso
\[\int f(x) \, dx = \int g(h(x))h'(x) \, dx = G(h(x)) + C\]¿¿¿Porqué es eso??? Bueno, simple: por definición, una antiderivada es una función de modo que cuando la diferencias, obtienes la función que estás integrando.
En este caso, si diferencia \( G(h(x)) \) obtiene
\[\displaystyle \frac{dG(h(x)}{dx} = G\,'(h(x))h'(x) = g(h(x))h'(x)\]por la Regla de la Cadena ..... y ¡shazam! lo tienes. Te dije que no fue tan difícil.
Ejemplos de métodos de sustitución
La mejor forma de aprender a integrar es practicando. Algunas personas se regocijarán al ver las pruebas, pero la mayoría querrá ver las cosas en la práctica.
Entonces, pasemos a los terrenos prácticos.
EJEMPLO 1
Encuentra la siguiente integral indefinida:
\[\int x \sin(x^2)\,dx\]RESPONDER:
Según el Paso 1, buscamos un bloque, un bloque muy específico. Si observa la integral, la variable de integración es \(x\).
Hay muchas pruebas y errores, potencialmente, al utilizar esta técnica. Digamos que consideramos el siguiente bloque:
\[u = x^2\]Sabemos que este bloque es bueno porque su derivada es \(u' = 2x\), que aparece en la integral.
Pero luego dices "Veo el \(x\) pero no veo el 2". Bueno, no hay necesidad de estar tenso. Podemos hacer un truco. Observa eso
\[\displaystyle \int x \sin(x^2)\,dx = \frac{1}{2}\int 2x \sin(x^2)\,dx\]¿Quién eres tú, Mandrake el mago? Bromas aparte, ese pequeño truco funciona. Entonces, la sustitución de bloque es
\[u = x^2\] \[du = 2x \, dx\](la notación de \(du = 2x \, dx\) es permisiva y técnicamente incorrecta, pero tiene una base sólida, así que tenga paciencia). Entonces, al hacer esta sustitución, transforme la integral en
\[\displaystyle \int x \sin(x^2)\,dx = \frac{1}{2}\int 2x \sin(x^2)\,dx \] \[\displaystyle = \frac{1}{2}\int \sin(u)\,du \] \[\displaystyle = -\frac{1}{2} \cos(u) + C \] \[\displaystyle = -\frac{1}{2} \cos(x^2) + C \]Entonces, una vez que cambió a la nueva variable \(u\), la integral se convirtió en una integral más fácil de resolver de \(\sin(u)\). Una vez que lo haya resuelto, DEBE recordar volver a la variable original.
EJEMPLO 2
Ahora, pasemos a un ejemplo un poco más complicado. Calcular la integral indefinida
\[\int e^{x+e^x} \,dx\]utilizando el método de sustitución de u.
RESPONDER:
¿Qué es esto que dices ??? Bueno, no es tan difícil. Observe que la integral indefinida se puede reescribir como:
\[\int e^{x+e^x} \,dx = \int e^x e^{e^x} \,dx \]Entonces, ahora que ve la nueva forma de la función que está integrando, ¿puede crear un "bloque" o una "sustitución en U"?
Recuerde, no dude en hacer prueba y error. Si algo no funciona, pruebe con otra cosa. ¿Y si probaras \(u = e^x\)?
La derivada del bloque es \(u' = e^x\), que se encuentra una vez en la función original. Además:
\[u = e^x\] \[du = e^x \, dx\]Entonces obtenemos:
\[\large \int e^{x+e^x} \,dx = \int e^x e^{e^x} \,dx \] \[\large = \int e^{e^x} e^x \,dx \] \[\large = \int e^{u} \,du \] \[\large = e^{u} + C\] \[\large = e^{e^x} + C\]Más sobre la integración por sustitución
Seamos realistas: la integración puede ser difícil. Realmente difícil. Algunas funciones no demasiado complicadas (al menos por lo que parece) han hecho que los matemáticos sean muy difíciles de manejar.
Algunas otras funciones no demasiado complicadas (al menos según las apariencias) simplemente no se pueden resolver con métodos elementales.
Por lo tanto, es mejor que crea que la integración puede ser una prueba difícil. Así que tienes que ir preparado.
Una de las herramientas más sencillas y la técnica más utilizada es la técnica de integración por sustitución. Sí, se usa porque aparece con frecuencia en exámenes o tareas.
Pero hicimos un poco de trampa. En realidad, las integrales que tienen la estructura adecuada para ser resueltas por la técnica de sustitución son muy específicas. La razón por la que ve muchos ejemplos de eso es porque son funciones muy específicas que deben funcionar para integrarse con esa técnica.
Pero permítame ser franco: si tiene un programa de software que está diseñado para generar funciones aleatorias, y genera una para usted, las posibilidades de que pueda utilizar la técnica de sustitución son escasas.
Aún así, es una pequeña y poderosa técnica de integración que funciona para una clase muy específica de integrales.
¿Qué es la técnica de sustitución en U?
La sustitución 𝘶 con integrales indefinidas es solo otro nombre para el método de sustitución. Se llama "sustitución 𝘶" porque el bloque que se utiliza se llama \(u\), por lo que la nueva variable será u.
Este definitivamente no es un buen nombre, porque el nombre que elija para su bloque es completamente irrelevante para el proceso de calcular la integral. Puede llamar al bloque (y su nueva variable) \(z\) y no haría ninguna diferencia.