Más información sobre esta calculadora gráfica de coseno

Esta calculadora le permitirá generar el gráfico para cualquier función de coseno, junto con el amplitud, periodo y frecuencia , mostrando todos los pasos. Debe proporcionar una función válida que involucre la función coseno. Podría ser algo trivial como cos(x), o puedes hacerlo más complicado como 2*cos(1/3 x + pi) - 4/5.

Una vez que proporcione una función válida que involucre coseno, simplemente haga clic en "Calcular" para obtener los resultados y todos los pasos del proceso que se muestran.

el coseno es uno Funcion trigonometrica que tiene una miríada de aplicaciones en Matemáticas y Física. Es muy común también en Geometría, cuando resolver triángulos .

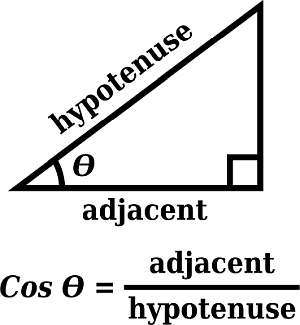
¿cómo hacer un gráfico cos?

El principio fundamental para graficar cualquier tipo de función es recurrir a una función simple conocida para la cual conocemos su gráfico y luego construir el gráfico que queremos encontrar en función de las traslaciones y el cambio de escala de este gráfico simple.

Para el caso de la gráfica cos, sabemos que la expresión más simple de una función coseno es f(x) = cos(x), la cual tiene una gráfica que se muestra a continuación:

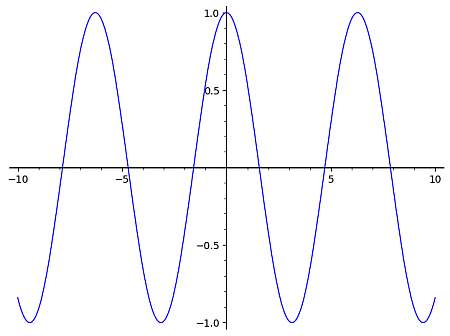
Luego, podemos usar este gráfico base para derivar el gráfico de funciones coseno más complejas, ya que la forma general será la misma, solo que se puede trasladar potencialmente a la izquierda o a la derecha, hacia abajo o hacia arriba, y el período también puede cambiar potencialmente, dependiendo de la función proporcionada.

¿cuáles son los pasos para graficar una función coseno?

• Paso 1 : Identifique la función cos que desea graficar en la forma a*cos(bx+c)+d si es posible
• Paso 2 : El valor de a corresponderá al amplitud , d son las unidades en las que el gráfico de cos básico se traslada hacia arriba, y el gráfico se desplaza -c/b a la derecha
• Paso 3 : Si la función cos no tiene la forma a*cos(bx+c)+d, cree una tabla de valores para x y f(x) (donde f(x) es la función cos dada) y calcule varias puntos que puede usar para trazar manualmente la forma del gráfico cos

De hecho, solo las funciones de la forma a*cos(bx+c)+d tendrán una expresión clara para la amplitud, el período, la frecuencia y las traslaciones, pero no son las únicas funciones de coseno que puede concebir. Por ejemplo, \(f(x) = cos(x^2)\) es una función coseno, pero no tiene período ni frecuencia, por ejemplo.

¿gráfico de cos versus gráfico de seno?

¿Qué tan similares son las gráficas de coseno y seno? Bueno, bastante parecido. Primero, observe que estamos hablando del gráfico básico de coseno y el gráfico de seno, esto es sin(x) y cos(x).

Luego, el gráfico de coseno se obtiene simplemente desplazando el gráfico de seno a las unidades \(\pi/2\) de la izquierda. Entonces, el gráfico de coseno y el gráfico de seno son esencialmente iguales, excepto por una traslación.

Con la gráfica en grados

¿Hay alguna diferencia entre la gráfica de coseno en radianes y la gráfica de coseno en grados? Bueno, hay una diferencia de escala, ya que cos completa un período completo en \(2\pi\) cuando se mide en radianes, y completa un período completo en 360 ^O cuando se mide en grados. Pero en cuanto a la forma, no hay una diferencia esencial.

¿cómo usar esta calculadora gráfica de cos?

Esta calculadora gráfica de cos elimina todas las conjeturas para usted, ya que todo lo que tiene que hacer es proporcionar una función de cos válida. Según el tipo de función cos que proporcione, tendrá un período, o tal vez el período no esté definido, en un caso como \(f(x) = cos(x^2)\), donde todavía decimos que tenemos un porque función .

Los gráficos de coseno, junto con los gráficos de seno y tangente, se encuentran entre los más comunes. gráficos trigonométricos que normalmente encuentras.

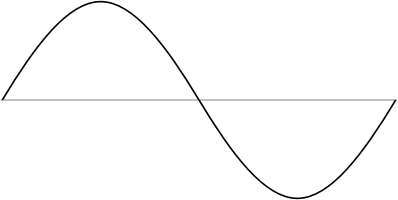
Ejemplo: gráfico coseno

Calcular la gráfica de : \(f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x - \frac{5}{6}\right)\)

Solución: Se ha proporcionado la siguiente función:

\[f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x - \frac{5}{6}\right)\]

Con base en el argumento de la función trigonométrica que se pasó, la frecuencia y el período se calculan de la siguiente manera:

\[ \begin{array}{ccl} \text{Period} & = & \displaystyle\frac{2\pi}{\frac{5}{4}} \\\\ \\\\ & \approx & 5.0265 \end{array}\]

y también

\[ \begin{array}{ccl} \text{Frequency} & = & \displaystyle\frac{\frac{5}{4}}{2\pi} \\\\ \\\\ & \approx & 0.1989 \end{array}\]

Por tanto, considerando la función trigonométrica proporcionada, \(f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x - \frac{5}{6}\right)\), obtenemos que:

» La amplitud en este caso es \(A = 1/3\).

» El cambio de fase es igual a \(\displaystyle\frac{\frac{5}{6}}{\frac{5}{4}} = 0.6667\).

» El desplazamiento vertical es igual a \( 0\).

Resumiendo, se ha encontrado lo siguiente para la función trigonométrica dada

• Período = \(5.0265\)
• Frecuencia = \(0.1989\)
• Amplitud = \(1/3\)
• Cambio de fase = \(0.6667\)
• Desplazamiento vertical = \(\displaystyle 0\)

El siguiente es el gráfico correspondiente.

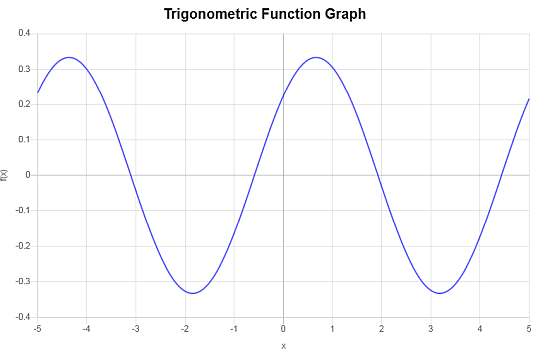
Ejemplo: más gráficos de coseno

¿La siguiente función es periódica? \(f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x^2 - \frac{5}{6}\right)\)

Solución: No, no lo es, debido al término \(x^2\).

Ejemplo: gráfico de coseno

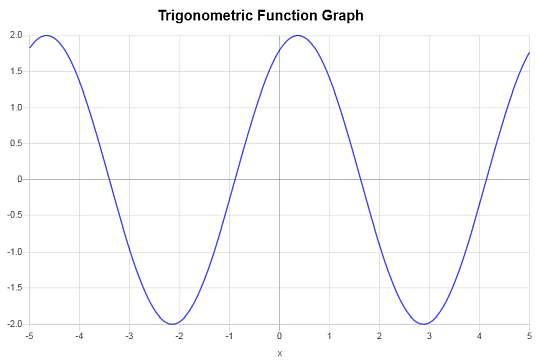
Calcular la gráfica de : \(f(x) = 2 \cos\left( \frac{5}{4}\left(x - \frac{7}{6}\right) + 1\right)\)

Solución: Tenga en cuenta que la expresión trigonométrica aprobada se puede simplificar de la siguiente manera:

entonces la función con la que trabajaremos es \(f(x) = 2\cos\left(\frac{5}{4}x-\frac{11}{24}\right)\).

Por lo tanto, con base en el argumento de la función trigonométrica que se pasó, la frecuencia y el período se calculan de la siguiente manera:

\[ \begin{array}{ccl} \text{Period} & = & \displaystyle\frac{2\pi}{\frac{5}{4}} \\\\ \\\\ & \approx & 5.0265 \end{array}\]

y también

\[ \begin{array}{ccl} \text{Frequency} & = & \displaystyle\frac{\frac{5}{4}}{2\pi} \\\\ \\\\ & \approx & 0.1989 \end{array}\]

Con base en la función trigonométrica proporcionada, \(f(x) = 2 \cos\left( \frac{5}{4}\left(x - \frac{7}{6}\right) + 1\right)\), obtenemos que:

» La amplitud en este caso es \(A = 2\).

» El cambio de fase es igual a \(\displaystyle\frac{\frac{11}{24}}{\frac{5}{4}} = 0.3667\).

» El desplazamiento vertical es igual a \( 0\).

Resumiendo, se ha encontrado lo siguiente para la función trigonométrica dada

• Período = \(5.0265\)
• Frecuencia = \(0.1989\)
• Amplitud = \(2\)
• Cambio de fase = \(0.3667\)
• Desplazamiento vertical = \(\displaystyle 0\)

El siguiente es el gráfico correspondiente.

Más calculadoras de geometría

Uno de los más útiles que puedes encontrar es este calculadora de periodo y frecuencia , para lo cual proporcionas cualquier función trigonométrica y te proporcionarán la amplitud, el periodo y la frecuencia.

Además, puedes usar este calculadora de pecado con pasos para trabajar con expresiones trigonométricas más complejas relacionadas con la función seno. El seno y el coseno son, de hecho, la piedra angular de todo lo relacionado con la geometría y la trigonometría.

Además, quizás te interese evaluar expresiones trigonométricas O graficar funciones trigonométricas en general.