Cómo utilizar esta calculadora del teorema de Pitágoras

1. Tiene tres casillas en las que puede introducir datos
2. Las formas representan los lados a y b, y la hipotenusa c
3. Por favor, escriba los valores de DOS de esas casillas
4. Por ejemplo, si sabes que los lados son a = 3 y b = 4, entonces escribes 3 en el primer formulario, y 4 en la segunda casilla
5. O, por ejemplo, si sabes que la hipotenusa es c = 10/3 y el lado a es 5, entonces escribes 5 en la primera forma, y 10/3 en la tercera casilla y dejas la segunda casilla vacía

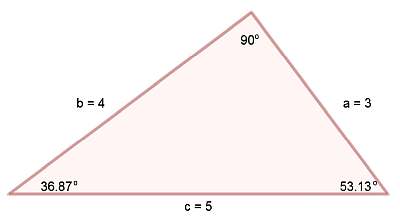
fórmula del teorema de pitágoras

La fórmula básica de Pitágoras es

\[\large a^2 + b^2 = c^2\]

y esta fórmula te dice cómo encontrar "c" si conoces "a" y "b".

Pero también, podrías encontrar "a" si conoces "c" y "b", y podrías resolver "b" si conoces "c" y "a".

Cómo se resuelven los triángulos rectos

Esta calculadora del teorema de Pitágoras le mostrará todos los pasos del cálculo de la fórmula del teorema de Pitágoras.

Esta no es sólo una calculadora de hipotenusa, ya que también puedes proporcionar un lado y la hipotenusa, y la calculadora te mostrará todos los pasos para obtener el otro lado.

La aplicación más típica es aquella en la que tienes dos lados en un triángulo rectángulo y quieres obtener la hipotenusa. Pero en última instancia, la idea en un triángulo rectángulo es que si tienes dos lados (en general), puedes obtener el tercer lado utilizando una versión de la fórmula de Pitágoras.

Así que con dos datos, puedes encontrar la longitud del lado que falta.

¿Es una calculadora de triángulos rectos solamente?

Sí, lo es. Esta calculadora sólo se ocupa de los triángulos rectos. Si tu triángulo no es recto, puedes usar esto Calculadora de triángulos SAS (donde se proporcionan dos lados y un ángulo, que puede ser cualquier ángulo, no necesariamente de 90 ^o .), este Calculadora de triángulos del SSS (donde conoces los tres lados y quieres encontrar todos los ángulos).

O bien, podría esto Calculadora de triángulos AAS (donde se conocen dos ángulos y el lado opuesto).

¿Cómo se calcula el teorema de Pitágoras?

Paso 1: En primer lugar, tienes que evaluar la información que tienes. ¿Tienes los dos lados a y b, y estás buscando la hipotenusa c? ¿O conoces c y a, o c y b?

Paso 2: Si conoces los dos lados a y b, esta calculadora de hipotenusa obtendrá la hipotenusa mediante la siguiente fórmula

\[c = \sqrt{a^2 + b^2}\]

y así se encuentra la hipotenusa.

Paso 3: Si conoces un lado y la hipotenusa, es decir, conoces a y c, ahora la calculadora obtendrá el otro lado, b, utilizando la siguiente fórmula

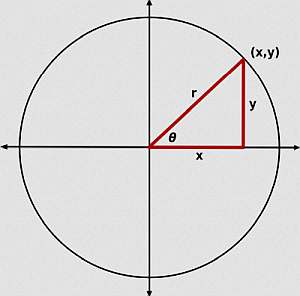
\[b = \sqrt{c^2 - b^2}\]

El ángulo de la calculadora del teorema de Pitágoras

Esta calculadora requiere que uno de los ángulos sea de 90 ^o para que la fórmula pitagórica sea válida.

¿Se puede utilizar Pitágoras para los ángulos? No, fíjate que esta calculadora pitagórica sólo se ocupa de los lados, y no calcula los ángulos.

Si quieres resolver completamente un triángulo (resolver un triángulo significa encontrar los lados y los ángulos), puedes utilizar estos: Calculadora de triángulos SAS , Calculadora de triángulos del SSS y Calculadora de triángulos AAS .

Ejemplo de cálculo de un triángulo rectángulo

Pregunta: Supongamos que los lados de un triángulo rectángulo son a = 3 y b = 3. Utiliza el Teorema de Pitágoras para calcular la hipotenusa c.

Solución: Nos han proporcionado dos lados, \(a =\displaystyle3\) y \(b = \displaystyle 6\). Tenemos que utilizar la fórmula pitagórica para calcular la hipotenusa \(c\).

A partir de esta información, hay que utilizar la siguiente fórmula pitagórica:

\[c = \displaystyle\sqrt{a^2 + b^2}\]

Así que ahora, enchufando los valores que tenemos disponibles, se obtiene lo siguiente:

\[c = \displaystyle\sqrt{a^2 + b^2} = \displaystyle\sqrt{3^2 + 6^2} = \displaystyle\sqrt{9 + 36} = \displaystyle\sqrt{45} = 3\sqrt{5}\]

Por tanto, y resumiendo, hemos comprobado que \(a = 3\), \(b = 6\) y \(c = 3\sqrt{5}\).