Álgebra Tutoriales

El teorema del binomio

El teorema del binomio es uno de los teoremas más famosos del álgebra y tiene multitud de aplicaciones en los campos del álgebra, probabilidad y estadística. Establece una fórmula agradable y concisa para la n ^th potencia de la suma de dos valores: \((a+b)^n\)

Sir Isaac Newton me presentó por primera vez de manera informal en 1665.

Muchos otros matemáticos notables han abordado el teorema del binomio después de Newton. Fue un problema muy atractivo en los siglos XVII y XVIII.

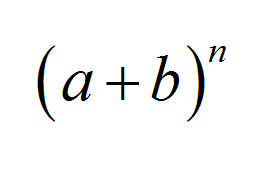
La fórmula de la expansión binomial

Lo que tiene de entero el teorema del binomio es que proporciona una fórmula muy elegante y concisa. Antes de entrar en la fórmula, hagamos algunos cálculos. Por ejemplo, para \(n = 2\) obtenemos:

\[\large (a+b)^2 = (a+b) \times (a+b) = a(a+b) + b(a+b) = a^2 + ba + ab + b^2 \] \[\large = a^2 + 2ab + b^2 \]

Ahora probemos con \(n = 3\):

\[\large (a+b)^3 = (a+b)^2 \times (a+b) = (a^2 + 2ab+b^2)(a+b) \] \[\large = a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3 \] \[\large = a^3 + 3a^2b + 3ab^2 + b^3\]

Finalmente, seamos valientes y probémoslo con \(n = 4\):

\[\large (a+b)^4 = (a+b)^3 \times (a+b) = (a^3 + 3a^2b + 3ab^2 + b^3)(a+b) \] \[\large = a^4 + 3a^3 b + 3a^2b^2 + ab^3 + a^3b + 3a^2b^2 + 3ab^3 + b^4 \] \[\large = a^4 + 4a^3b + 6 a^2 b^2 + 4a b^3 + b^4\]

Ok, eso fue valiente, ¿verdad? ¿Ves algún patrón allí? Puedo ver algunos. Por ejemplo, para \(n = 2\) podríamos simplificarlo a 3 términos. Para \(n = 3\) podríamos simplificarlo a 4 términos, y para \(n = 4\) podríamos simplificarlo a 5 términos. Entonces, en general, espero que para el poder general de \(n\), tengamos \(n+1\) términos

¿Más patrones? Bueno, siempre hay un término de la forma \(a^l b^m\), y podemos ver que las potencias \(l\) van disminuyendo y las potencias \(m\) van aumentando. Pero también hay algo interesante: si marca cada término, la suma de potencias es siempre \(n\). De hecho, comprobará que \(l + m = n\) para todos esos términos.

Por ejemplo, para \(n = 2\) tiene el término \(2 a b\). La potencia de \(a\) es 1, la potencia de \(b\) es 1 y la suma de potencias es \(1 + 1 = 2\). O, por ejemplo, para \(n = 4\) tienes el término \(6 a^2 b^2\), donde la potencia de \(a\) es 2 y la potencia de \(b\) es 2, y la suma de potencias es \(2 + 2 = 4\)

El teorema general del binomio

Ahora estamos listos para dar la expresión general del teorema del binomio. Listo? Tenemos:

\[\large (a+b)^n = a^n + {n \choose 1} a^{n-1} b + {n \choose 2} a^{n-2} b^2 + ... + {n \choose n-1} a b^{n-1} + b^n \]

donde el término \({n \choose i}\) se lee como "n elige i" o también como un "coeficiente combinatorio", y se define como

\[\large \displaystyle {n \choose i}= \frac{n!}{i! \times (n-i)!}\]

Por ejemplo,

\[\large \displaystyle {5 \choose 2} = \frac{5!}{2! \times (5-2)!} = \frac{5!}{2! \times 3!} = \frac{120}{2 \times 6} = 10\]

Puedes usar esto calculadora de coeficientes combinatorios para aprender más sobre él y practicar viendo todos los pasos que se muestran.

El teorema general del binomio usando una suma

La suma anterior que define el teorema del binomio usa la notación por extensión, para hacer los términos más comprensibles. Como siempre en Matemáticas, tratamos de hacer las cosas más compactas, y la expresión anterior se puede resumir como:

\[\large \displaystyle (a+b)^n = \sum_{i=0}^n {n \choose i} a^i b^{n-i} \]

Observe los poderes de los términos en la expansión. El término general es \(a^i b^{n-i}\) (multiplicado por una constante). La suma de las potencias es \(i + (n-i) = n\). Entonces, la suma de las potencias de TODOS los términos en la expansión debe ser \(n\). ¿No es bonito ???

EJEMPLO 1

¿Puede el término \(x^3 y^2\) (multiplicado por una constante) ser parte de la expansión de \((x+y)^6\)? ¿Por qué?

RESPONDER:

La respuesta es no. En este caso, \(n = 6\), y sabemos por el teorema del binomio que la suma de las potencias de los términos \(x^l y^m\) en la expansión debe ser igual a \(n\). En este caso, \(l + m = 3 + 2 = 5\), que no es lo mismo que \(n = 6\). Por tanto, el término \(x^3 y^2\) (multiplicado por una constante) no puede ser parte de la expansión de \((x+y)^6\).

EJEMPLO 2

Expanda \((a-b)^3\) usando el teorema del binomio.

RESPONDER:

Espere. Debes estar pensando "Me acabas de enseñar cómo expandir \((a+b)^n\), pero ahora me preguntas por \((a-b)^n\). ¿Por qué eres tan cruel?". Espere. No te estoy engañando.

Siempre hay un truco (no olvides esa línea, aparece mucho en matemáticas).

Observe que \(a - b\) es lo mismo que \(a + (-b)\).

Ahhhhhhh, entonces el teorema del binomio todavía se aplica. Por lo que entonces:

\[\large (a-b)^3 = (a+(-b))^3 = a^3 + {3 \choose 1} a^2 (-b) + {3 \choose 2} a (-b)^2 + (-b)^3 \] \[\large \displaystyle = a^3 - \frac{3!}{1! \times 2!} a^2 b + \frac{3!}{2! \times 1!} a b^2 -b^3 \] \[\large \displaystyle = a^3 - \frac{6}{1 \times 2} a^2 b + \frac{6}{2 \times 1} a b^2 -b^3 \] \[\large = a^3 - 3 a^2 b + 3 a b^2 -b^3 \]

Más sobre la expansión binomial

El teorema del binomio es tan importante que se cubre en la mayoría de los cursos, incluidos Álgebra, Cálculo, Probabilidad y Estadística.

Hay algunas generalizaciones como la expansión binomial negativa, que está más allá del alcance de este tutorial.

El Triángulo de Pascal

Algunas veces los estudiantes se atascan cuando necesitan calcular las constantes (los coeficientes combinatorios) que van en la expansión binomial. Una forma realmente fácil de hacerlo es utilizar el Triángulo de Pascal.

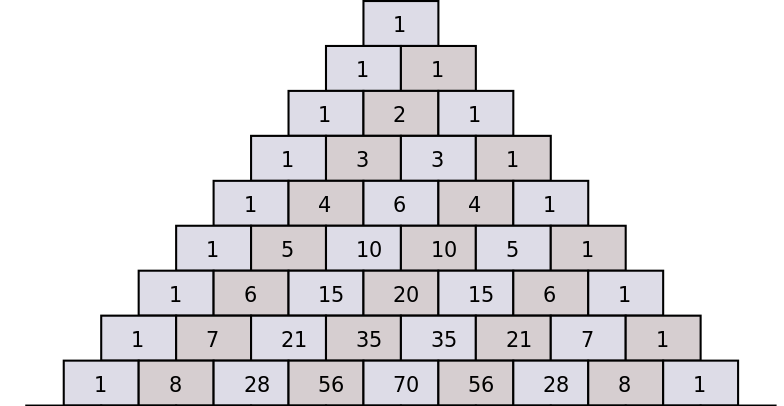
El triángulo de Pascal muestra cómo se pueden calcular los coeficientes binomiales sucesivos en base a los coeficientes del valor anterior de \(n\), sumando los dos coeficientes que vienen inmediatamente arriba.

Aplicaciones

La expansión binomial tiene múltiples aplicaciones en álgebra y en teoría de probabilidades. Por ejemplo, en Probabilidad, la distribución binomial se basa en el teorema del binomio.

De hecho, considere un número \(0 \le p \le 1\). Luego, \(p + (1-p) = 1\) y podemos usar el teorema del Binomio:

\[\large \displaystyle 1 = 1^n = (p + (1-p))^n = \sum_{i=0}^n {n \choose i} p^i (1-p)^{n-i} \]

Lo que significa que

\[\large \displaystyle \sum_{i=0}^n {n \choose i} p^i (1-p)^{n-i} = 1 \]

Resulta que cada uno de los términos \({n \choose i} p^i (1-p)^{n-i}\) representa una probabilidad. Además, tenemos:

\[\large \Pr(X = i) = {n \choose i} p^i (1-p)^{n-i} = 1 \]

donde \(X\) es el número de éxitos después de \(n\) pruebas, cuando la probabilidad de éxito de cada prueba es \(p\). La variable \(X\) se conoce como la variable aleatoria binomial.