Calculadora de probabilidad de poisson

Más información sobre el Probabilidad de distribución de Poisson para que pueda usar mejor la calculadora de Poisson anterior: El Probabilidad de veneno es un tipo de distribución de probabilidad discreta que puede tomar valores aleatorios en el rango \([0, +\infty)\). Las principales propiedades de la distribución de Poisson son:

• Es discreto y puede tomar valores de 0 a \(+\infty\).


• El tipo de asimetría depende de la media de la población (\(\lambda\))


• Está determinado por la media de la población (\(\lambda\))


• Su media es \(\lambda\) y su varianza poblacional también es \(\lambda\)

Cómo usar la calculadora de distribución de poisson

Utilizando lo anterior Calculadora de la curva de distribución de Poisson , puede calcular probabilidades de la forma \(\Pr(a \le X \le b)\), de la forma \(\Pr(X \le b)\) o de la forma \(\Pr(X \ge a)\).

Escriba el parámetro apropiado para \(\lambda\) en el cuadro de texto de arriba, seleccione el tipo de cruz, especifique su evento y calcule su probabilidad de Poisson. Observe que \(\lambda\) corresponde a la media poblacional de la distribución.

¿cómo se calcula la probabilidad de poisson?

La fórmula de distribución de probabilidad de Poisson es

\[ \Pr(X = k) = \displaystyle \frac{e^{-\lambda} \lambda^k}{k!}\]

No existe una expresión simple o corta para expresar la Fórmula CDF de Poisson , que se obtiene sumando los valores de probabilidad individuales hasta un determinado valor umbral.

¿cómo encuentras la probabilidad de poisson entre dos números?

Esencialmente, debe evaluar la fórmula de poisson acumulativa (cdf) en los puntos finales, que serían los dos números, digamos k y m. Pero dado que la distribución es discreta, lo que calcula es F(m) - F(k-1), donde F es la función cdf de Poisson.

Ahora, si usa nuestra calculadora, no tiene que preocuparse por eso, y solo proporcione los dos números en el formulario de arriba.

Cómo calcular la distribución de poisson calculadora excel

Excel tiene una fórmula, la fórmula "=POISSON()" que permite obtener el pdf o el cdf de Poisson.

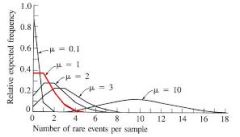
¿hay alguna diferencia entre la distribución de poisson y la binomial?

Sí, hay claras diferencias. En primer lugar, no son la misma distribución. Aunque ambos son discretos (toman valores que se pueden numerar, como 0, 1, 3, 4, etc.), tienen algunas diferencias fundamentales.

por ejemplo, el distribución de veneno está determinada por un solo parámetro, que es su media \(\lambda\). Por otro lado, el Distribución Binomial requiere de un tamaño de muestra N, y la probabilidad de éxito.

Una similitud interesante es que las distribuciones de probabilidad de Poisson y Binomial se pueden aproximar estrechamente con la distribución normal bajo ciertas circunstancias (tamaño de muestra suficientemente grande).

De hecho, puede comprobarlo con nuestro aproximación normal para el binomio y aproximación normal para la distribución de Poisson .

Ventajas de esta calculadora de poisson

1. Aunque Excel puede ayudarlo con la mayoría de sus cálculos de estadísticas, esta calculadora le muestra todos los pasos
2. Al ver los pasos, puede comprender mejor el proceso del cálculo de probabilidades.
3. En última instancia, todas las distribuciones discretas siguen la misma lógica para calcular las probabilidades

Ejemplo: usos de esta calculadora de probabilidad de distribución de poisson

Pregunta : Suponga que una variable X tiene una distribución de Poisson con media 3.4. Encuentra la siguiente probabilidad: \(\Pr(3 \le X \le 6)\).

Solución:

Necesitamos calcular la probabilidad de una distribución binomial. Se proporciona la siguiente información:

Population Mean \((\lambda)\) =	\(3.4\)
Probability Event =	\(\Pr(3 \le X \le 6) \)

Necesitamos calcular \(\Pr(3 \le X \le 6)\). Por tanto, se obtiene lo siguiente:

\[ \Pr(3 \le X \le 6) = \sum_{i=3}^{ 6} {\Pr(X = i)} = \Pr(X = 3) + \Pr(X = 4) + \Pr(X = 5) + \Pr(X = 6) \] \[ = 0.2186 + 0.1858 + 0.1264 + 0.0716 \]\[= 0.6024 \]

que completa el cálculo.

Otra calculadora de distribución de probabilidad discreta

Esta calculadora de distribución de Poisson con pasos corresponde a un salculadora para una distribución discreta. Tenemos otras calculadoras de distribución discreta que le pueden interesar, como nuestra Calculadora de la distribución binomial , calculadora de distribución geométrica , y Calculadora de distribución hipergeométrica , por mencionar algunos de ellos.

Además, puede utilizar nuestro calculadora de probabilidad discreta general que le proporcionará la media y la desviación estándar de una distribución discreta genérica.