Calculadora de probabilidad binomial

Más información sobre el probabilidad de la distribución binomial para que pueda usar mejor esta calculadora binomial: La probabilidad binomial es un tipo de distribución de probabilidad discreta que puede tomar valores aleatorios en el rango de \([0, n]\), donde \(n\) es el tamaño de la muestra.

Propiedades de la probabilidad binomial

Las principales propiedades de la distribución binomial son:

• Es discreto, y puede tomar valores de 0 a n, donde n es el tamaño de la muestra


• El tipo de asimetría depende de los parámetros n y p


• Se determina mediante dos parámetros: la proporción poblacional de éxito p, el tamaño de la muestra n (o número de ensayos)


• El media de la distribución binomial es \(n\cdot p\) y su desviación estándar es \(\sqrt{np(1-p)}\)

¿qué es la fórmula de la probabilidad binomial?

La fórmula que define la probabilidad binomial (que se llama su función de distribución de probabilidad ) es:

\[\Pr(X = k) = \left( \begin{matrix} n \\\\ k \end{matrix} p^k \cdot (1-p)^{n-k} \]

donde n y p son los parámetros correspondientes de la distribución. Esto es, n es el número de intentos y p es la probabilidad de éxito de cada intento.

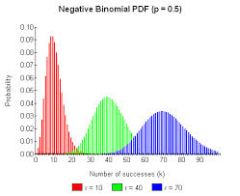
Cómo utilizar esta calculadora de la distribución binomial con pasos

Utilizando lo anterior calculadora de la curva de distribución binomial , podemos calcular probabilidades de la forma \(Pr(a \le X \le b)\), de la forma \(\Pr(X \le b)\) o de la forma \(\Pr(X \ge a)\). Cualquier otro tipo de evento se puede derivar de estos tipos elementales de eventos.

Por ejemplo, es posible que desee encontrar la probabilidad de que X esté entre 0 y 1 o entre 3 y 4. Esa probabilidad la calcularía como \( \Pr(0 \le X \le 1) + \Pr(3 \le X \le 4)\)

Escriba los parámetros apropiados para \(n\) y \(p\) en el cuadro de texto de arriba, seleccione el tipo de cruz, especifique su evento y calcule su probabilidad binomial, mostrando todos los detalles paso a paso de la fórmula de probabilidad binomial.

Otras calculadoras de distribución de probabilidad importantes

La distribución binomial es un tipo de distribución discreta. Otras calculadoras disponibles para las distribuciones discretas son nuestras Calculadora de la distribución de Poisson , calculadora hipergeométrica o nuestro calculadora de distribución geométrica .

¿qué ocurre cuando la probabilidad de éxito no es constante?

Una forma generalizada del coeficiente binomial es el coeficiente multinomial , que considera combinaciones de números \(k\) que suman \(n\), con \(k \ge 2\).

Ahora bien, si se trata de una distribución continua, tal vez le interese consultar nuestro calculadora de probabilidad normal online , que trata de la distribución normal y eventos relacionados, que es la distribución continua más común.

Ejemplo: cálculo de probabilidades binomiales

Pregunta : Supongamos que X es una variable aleatoria con distribución binomial, con parámetros n = 10 y p = 0,45. Calcule \(\Pr(2\le X\le 4)\).

Solución:

Necesitamos calcular la probabilidad de una distribución binomial. Se proporciona la siguiente información:

Population Probability of Success \((p)\) =	\(0.45\)
Sample Size \((n)\) =	\(10\)
Probability Event =	\(\Pr(2 \leq X \leq 4) \)

Esto implica que

\[\Pr(2 \le X \le 4) = \Pr(X = 2) + \Pr(X = 3) + \Pr(X = 4)\]\[= \left( \begin{matrix} 10 \\\\ 2 \end{matrix}\right) 0.45^{ 2} \cdot 0.55^{ 10-2} + \left( \begin{matrix} 10 \\\\ 3 \end{matrix}\right) 0.45^{ 3} \cdot 0.55^{ 10-3} + \left( \begin{matrix} 10 \\\\ 4 \end{matrix}\right) 0.45^{ 4} \cdot 0.55^{ 10-4}\]\[= 0.0763 + 0.1665 + 0.2384\] \[= 0.4811\]

lo que significa que la probabilidad que buscamos es \(\Pr(2 \leq X \leq 4) = 0.4811 \).