Der t-test für gepaarte proben

Mehr über die T-Test für Zwei Abhängige Probe Sie können also die vom Solver lieferten Ergebnisse besser verstehen.

Wie berechnet man einen gepaarten t-test?

Ein T-Test für zwei gepaarte Proben ist ein Hypothesentest, der versucht, eine Behauptung über die Bevölkerung zu erheben (\(\mu_1\) und \(\mu_2\)).Insbesondere verwendet ein T -Test Beispielinformationen, um zu beurteilen, wie plausibel es für Differenz \(\mu_1\) - \(\mu_2\) gleich Null ist.

Der Test hat zwei nicht überlappende Hypothesen, die Null und die alternative Hypothese.Die Nullhypothese ist eine Aussage über den Populationsparameter, der keine Wirkung anzeigt, und die alternative Hypothese ist die komplementäre Hypothese zur Nullhypothese.Die Idee des Tests ist zu beurteilen, ob es statistische Bedeutung gibt oder nicht.Die Haupteigenschaften des T-Tests für zwei gepaarte Proben sind:

• Der Test erforderte zwei abhängige Proben, die tatsächlich gepaart oder übereinstimmen oder mit wiederholten Maßnahmen zu tun haben (Maßnahmen aus denselben Probanden)


• Wie bei allen Hypothesen-Tests kann der T-Test abhängig von unserem Wissen über die Situation "No Effect" zweiseitig, links oder rechtsschwanz werden


• Das Hauptprinzip der Hypothesentests ist, dass die Nullhypothese abgelehnt wird, wenn die erhaltene Teststatistik unter der Annahme, dass die Nullhypothese wahr ist, ausreichend unwahrscheinlich ist


• Der p-Wert ist die Wahrscheinlichkeit, Probenergebnisse als extrem oder extremer zu erhalten als die erhaltenen Probenergebnisse, unter der Annahme, dass die Nullhypothese wahr ist


• In einer Hypothesentests gibt es zwei Arten von Fehlern.Typ I -Fehler tritt auf, wenn wir eine echte Nullhypothese ablehnen, und der Fehler vom Typ II tritt auf, wenn wir keine falsche Nullhypothese ablehnen

Wie berechnen sie manuell einen gepaarten t-test?welche formel verwenden sie?

Die Formel für eine T-Statistik für zwei abhängige Proben lautet:

\[t = \frac{\bar D}{s_D/\sqrt{n}}\]

wobei \(\bar D = \bar X_1 - \bar X_2\) die mittlere Differenz und \(s_D\) ist die Stichprobenstandardabweichung der Unterschiede \(\bar D = X_1^i - X_2^i\) für \(i=1, 2, ... , n\).

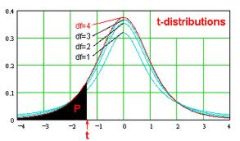
So verwenden sie eine gepaarte t-test-formel

• Schritt 1: Zuerst müssen Sie definieren, was Ihre Null- und alternativen Hypothesen sind.Die Auswahl ist zweiseitig, links oder rechter Schwanz.
• Schritt 2: Anschließend müssen Sie Ihr Bedeutungsniveau angeben.Normalerweise wählen Sie α = 0,05.Dies ist die Toleranz, die Sie akzeptieren, um einen Fehler vom Typ I zu machen
• Schritt 3: Basierend auf dem von Ihnen gewählten Signifikanzniveau und der Art des Schwanzes finden Sie die kritischen T-Statistiken, indem Sie entweder eine T-Distribution-Tabelle betrachten oder einen Taschenrechner oder einen Excel verwenden.Dann geben Sie Ihre Ablehnungsregion eindeutig an
• Schritt 4: Sie berechnen die T-Statistik mit der oben angegebenen Formel t = dbar/(SD/√n)
• Schritt 5: Basierend auf dem berechneten T-Statistik und ob es in die Ablehnungsregion fällt oder nicht, bestimmen Sie, ob Sie die Nullhypothese ablehnen oder nicht
• Schritt 6: Verwenden Sie die Schlussfolgerung des T-Tests, um im Kontext der Einstellung des spezifischen Problems eine Interpretation zu geben.

Paired t -testbeispiel

Frages : Angenommen, Sie haben die folgende Stichprobe gepaarter Daten.

	Sample 1	Sample 2	Difference = Sample 1 - Sample 2
	4	2	2
	5	3	2
	6	4	2
	5	5	0
	4	6	-2
	3	4	-1
	5	3	2
Average	4.571	3.857	0.714
St. Dev.	0.976	1.345	1.704
n	7	7	7

Kann die Nullhypothese, dass der mittlere Bevölkerungsdifferenz bei 0,05 Signifikanzniveau Null abgelehnt wird.

Lösung:

Aus den Stichprobendaten wurde festgestellt, dass die entsprechenden Stichproben mit:

\[\bar X_1 = 4.571\]\[\bar X_2 = 3.857\]

Auch die bereitgestellten Beispiel -Standardabweichungen sind:

\[ s_1 = 0.976 \]\[ s_2 = 1.345 \]

und die Stichprobengröße beträgt n = 7. Für die Score -Unterschiede, die wir haben

\[ \bar D = 0.714 \]\[ s_D = 1.704 \]

(1) Null-und alternative Hypothesen

Die folgenden Null- und alternativen Hypothesen müssen getestet werden:

\[ \begin{array}{ccl} H_0: \mu_D & = & 0 \\\\ \\\\ H_a: \mu_D & \ne & 0 \end{array}\]

Dies entspricht einem zweiseitigen Test, für den ein T-Test für zwei gepaarte Proben verwendet wird.

(2) Fähigsregion

Basierend auf den bereitgestellten Informationen ist die Signifikanzstufe \(\alpha = 0.05\) und der kritische Wert für einen zweiseitigen Test ist \(t_c = 2.447\).

Die Ablehnungsregion für diesen zweiseitigen Test ist \(R = \{t: |t| > 2.447\}\)

(3) Teststatistik

Die T-Statistik wird wie folgt berechnet:

\[ \begin{array}{ccl} t & = & \displaystyle \frac{\bar D}{s_D/ \sqrt n} \\\\ \\\\ & = & \displaystyle \frac{0.714}{1.704/ \sqrt{7}} \\\\ \\\\ & = & 1.109 \end{array}\]

(4) Inner

Da beobachtet wird, dass \(|t| = 1.109 \le t_c = 2.447\), wird dann zu dem Schluss gekommen, dass Die Nullhypothese Wird Nicht Abgelehnt.

Unter Verwendung des p-Wert-Ansatzes: Der p-Wert ist \(p = 0.31\), und da \(p = 0.31 \ge 0.05\) wird der Schluss gezogen, dass die Nullhypothese nicht abgelehnt wird.

(5) Fazit

Es wird der Schluss gezogen, dass die Nullhypothese HO Wird Nicht Abgelehnt. Daher gibt es nicht genügend Beweise, um zu behaupten, dass die Bevölkerungsdifferenz \(\mu_D = \mu_1 - \mu_2\) auf dem \(\alpha = 0.05\) Signifikanzniveau von 0 unterscheidet.

Konfidenzintervall

Das 95% -Konfidenzintervall ist \(-0.862 < \mu_D < 2.291\).

Was ist die nichtparametrische alternative des gepaarten t-tests?

Dies ist ein parametrischer Test, der nur dann verwendet werden sollte, wenn die Normalitätsannahme erfüllt ist.Wenn es fehlschlägt, sollten Sie dies stattdessen verwenden Wilcoxon Signierte Rangstest .Dieser gepaarte T-Test-Rechner befasst sich mit der mittleren und Standardabweichung von Paaren.

Andere t-test-anwendungen

Oft haben Sie zwei Proben, die nicht gepaart werden. In diesem Fall würden Sie a verwenden T-Test für Zwei Unabhängige Probenrechner .Beachten Sie, dass in diesem Fall die Proben nicht unbedingt die gleiche Größe haben müssen.