So verwenden sie diesen t-test-rechner für eine probe

Mehr über die T-Test für Sie können also die von diesem Löser erzielten Ergebnisse besser interpretieren: Ein T-Test für einen Mittelwert ist ein Hypothesentest, der versucht, einen Anspruch auf das Bevölkerungsniveau zu erheben (\(\sigma\)).Dieser T-Test muss im Gegensatz zum Z-Test die Bevölkerungsstandardabweichung nicht kennen \(\sigma\).

Wie kann man einen t-test für eine bevölkerung bedeuten?

Der Test hat zwei komplementäre Hypothesen, die Null und die alternative Hypothese.Die Nullhypothese ist eine Aussage über das Bevölkerungsniveau unter der Annahme einer Wirkung, und die alternative Hypothese ist die komplementäre Hypothese zur Nullhypothese.Die Haupteigenschaften eines T-Tests mit einem Stichproben für eine Population sind:

• Für einen T-Test für einen Mittelder Freiheit (anstatt die Standardnormalverteilung zu sein, wie im Fall eines Z-Tests für einen Mittelwert)


• Abhängig von unserem Kenntnis


• Das Hauptprinzip der Hypothesentests ist, dass die Nullhypothese abgelehnt wird, wenn die erhaltene Teststatistik unter der Annahme, dass die Nullhypothese wahr ist, ausreichend unwahrscheinlich ist


• Der p-Wert ist die Wahrscheinlichkeit, Probenergebnisse als extrem oder extremer zu erhalten als die erhaltenen Probenergebnisse, unter der Annahme, dass die Nullhypothese wahr ist


• In einer Hypothesentests gibt es zwei Arten von Fehlern.Typ I -Fehler tritt auf, wenn wir eine echte Nullhypothese ablehnen, und der Fehler vom Typ II tritt auf, wenn wir keine falsche Nullhypothese ablehnen

Wie berechnet ich die t-statistik für eine probe?

Was ist also die einzige Probe -Testformel?In diesem Fall ist für diese T-Test-Formel für die T-Statistik

\[t = \frac{\bar X - \mu_0}{s/\sqrt{n}}\]

Die Nullhypothese wird abgelehnt, wenn die T-Statistik in der Ablehnungsregion liegt, die durch das Signifikanzniveau (\(\alpha\)) der Art des Schwanzes (zweiseitige, linksschwanze oder rechte Schwanz) und die bestimmt wird ANZAHL DER FEIHEITSGRADE \(df = n - 1\)

Was passiert mit dem t-test, wenn ich 2 proben habe

Beachten Sie, dass dies ein Testrechner mit einem Proben -T -Test ist.Wenn Sie stattdessen zwei Mittel vergleichen müssen, sollten Sie a verwenden T-Test für unabhängige Probe , stattdessen.

In ähnlicher Weise haben Sie möglicherweise zwei Stichproben, aber sie werden gepaart, übereinstimmen oder wiederholt. In diesem Fall ist das entsprechende Werkzeug dies zu verwenden Gepaarter t -zestechner , wenn das der Fall ist.

Entscheidung für einen beispiel-t-test

Wie treffen Sie eine Entscheidung über einen T-Test mit einer Stichprobe?Zuerst müssen Sie die T-Statistik kennen, die wir \(t_{obs}\) und die Freiheitsgrade df nennen, damit Sie den p-Wert berechnen können.

Der Berechnungsprozess des p-Werts hängt von der Art der definierten Schwänze ab.Für einen zweiseitigen Test wird der p-Wert als \(p = \Pr(|t_{df}| > |t_{obs}|)\) berechnet.Für einen Test mit dem linken Schwanz wird der p-Wert als \(p = \Pr(t_{df} < t_{obs})\) berechnet, und für einen Test mit rechtsschwanzer Test wird der p-Wert als \(p = \Pr(t_{df} > t_{obs})\) berechnet.

Ein beispiel-t-test-beispiel

Ein Anbieter hat Aufzeichnungen, aus denen hervorgeht, dass der durchschnittliche Kunde im Durchschnitt 80 Dollar in ihrem Geschäft ausgibt, aber in letzter Zeit ist sie der Ansicht, dass dieser Betrag gestiegen ist.Sie sammelt eine zufällige Stichprobe von n = 30 Kunden und stellt fest, dass der durchschnittliche Betrag, der für das Geschäft ausgegeben wurde, 85,4 USD betrug, mit einer Stichprobenstandardabweichung von 12,4 USD.Hat sie genügend Beweise, um zu behaupten, dass der Durchschnitt, der für ihren Laden ausgegeben wurde, bei 0,05 Signifikanzniveau erheblich zugenommen hat?

Lösung:

Die folgenden Informationen wurden bereitgestellt:

Hypothesized Population Mean \((\mu)\) =	\(80\)
Sample Standard Deviation \((s)\) =	\(12.4\)
Sample Size \((n)\) =	\(30\)
Sample Mean \((\bar X)\) =	\(85.4\)
Significance Level \((\alpha)\) =	\(0.05\)

(1) Null-und alternative Hypothesen

Die folgenden Null- und alternativen Hypothesen müssen getestet werden:

\[ \begin{array}{ccl} H_0: \mu & = & 80 \\\\ \\\\ H_a: \mu & > & 80 \end{array}\]

Dies entspricht einem rechtsschwanzigen Test, für den ein T-Test für einen Mittelwert mit unbekannter Bevölkerungsstandardabweichung unter Verwendung der Stichprobenstandardabweichung verwendet wird.

(2) Fähigsregion

Basierend auf den bereitgestellten Informationen ist die Signifikanzniveau \(\alpha = 0.05\) und der kritische Wert für einen Test mit rechtsschwächen \(t_c = 1.699\).

Die Ablehnungsregion für diesen rechtsschwanzigen Test ist \(R = \{t: t > 1.699\}\)

(3) Teststatistik

Die T-Statistik wird wie folgt berechnet:

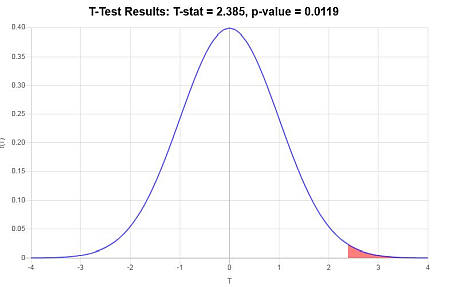
\[ \begin{array}{ccl} t & = & \displaystyle \frac{\bar X - \mu_0}{s/\sqrt{n}} \\\\ \\\\ & = & \displaystyle \frac{ 85.4 - 80}{ 12.4/\sqrt{ 30}} \\\\ \\\\ & = & 2.385 \end{array}\]

(4) Inner

Da beobachtet wird, dass \(t = 2.385 > t_c = 1.699\), wird dann zu dem Schluss gekommen, dass Die Nullhypothese Wird Abgelehnt.

Verwenden des p-Wert-Ansatzes: Der p-Wert ist \(p = 0.0119\), und da \(p = 0.0119 < 0.05\) wird der Schluss gezogen, dass die Nullhypothese abgelehnt wird.

(5) Fazit

Es wird der Schluss gezogen, dass die Nullhypothese HO Ist Abgelehnt. Daher gibt es nicht genügend Beweise, um zu behaupten, dass die Bevölkerung bei \(\mu\) bei \(\alpha = 0.05\) Signifikanzniveau größer als 80 ist.

Konfidenzintervall

Das 95% -Konfidenzintervall ist \(80.77 < \mu < 90.03\).

Grafisch