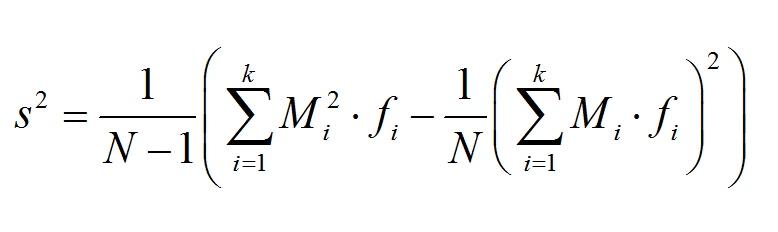Eine möglichkeit, varianzrechneranalyse

Mehr über die Einweg-Anova-Test Sie können also die Ergebnisse dieses Lösers besser verstehen.Zunächst ist ANOVA oder Analyse von Varianzen eines der wichtigsten Bereiche in der Statistik.Der Grund dafür ist, dass der Kern der Analyse der Variation gezeigten Stichproben durch Aufschlüsse der Gesamtvariation in verschiedene Variationsquellen unterteilt wird.

Die grundlegendste Verwendung von ANOVA besteht darin, den Unterschied zwischen den Populationen für mehrere Gruppen (2 oder mehr) zu testen.Erinnern wir uns daran, dass ein T-Test verwendet wird, um die Mittel von zwei Gruppen zu vergleichen. Dann ist ANOVA eine Sortiererweiterung, die es ermöglicht, Vergleiche für zwei oder mehr Gruppen durchzuführen.

Wie bei jedem anderen Hypothesentest verwendet ANOVA einen Null und die alternative Hypothese.Die Nullhypothese ist eine Aussage, die behauptet, dass alle Bevölkerungsmittelmittel gleich sind, und die alternative Hypothese ist die Hypothese, dass nicht alle Mittel gleich sind.ist ungleich).

Wie berechnet man eine anova?

Das Ausführen eines ANOVA -Tests ist ein wenig wie das Ausführen eines anderen parametrischen Tests, und Sie müssen dann einige Annahmen erfüllen.Die wichtigsten Annahmen, die für die Durchführung einer Einweg-ANOVA erforderlich sind, sind:

• Die abhängige Variable (DV) muss zumindest in Intervallebene gemessen werden


• Die Gruppen müssen von normal verteilten Populationen stammen


• Die Gruppen müssen aus normalerweise Bevölkerungsgruppen mit gleicher Bevölkerungsvarianzen stammen

Wenn die Ergebnisse der ANOVA signifikant sind, ist dies die Nullhypothese abgelehnt, können wir a durchführen Post-Hoc-Test Um genau zu beurteilen, welche Paare signifikant unterscheiden.Beispiele für Post-hoc-Tests sind Fisher's LSD, Tukeys Test, Bonferroni-Korrektur usw.

Die Nullhypothese eines ANOVA -Tests wird abgelehnt, wenn die F-Statistik überschreitet den Wert der Kritsches F-Verhältnis Das wird berechnet, basierend auf den entsprechenden Freiheitsgraden.

Wenn Sie K -Gruppen und eine Gesamtstichprobengröße von N haben, sind die Zählergrade DFN = K - 1 und die Nenner -Freiheitsgrade dfd = n - k - 2.

Wenn einige der Annahmen nicht erfüllt sind (insbesondere die zweite sind dritter), gibt es Korrekturoptionen für einige robustere Statistiken.Wenn die Annahmen schwerwiegende Verstöße haben, wäre es angemessener, eine nichtparametrische Alternative wie den Test von Kruskal-Wallis zu verwenden.

Dieser ANOVA-Rechner mit Schritten bietet Ihnen genügend Informationen, um die Nullhypothese abzulehnen oder nicht abzulehnen, basierend auf dem berechneten F-Verhältnis.Wenn die Nullhypothese berechnet wird, müssen Sie einen Post-hoc-Test durchführen.

Warum ein t-test stattdessen nicht verwendet wird

Zwei unabhängige Stichproben-T-Tests sind so konzipiert, dass sie Vergleiche zwischen zwei Gruppen durchführen.Wenn Sie mehr als zwei Gruppen haben, besteht die einzige Möglichkeit, mehrere paarweise Vergleiche durchzuführen.

Jeder dieser paarweisen Vergleiche hat eine gewisse Wahrscheinlichkeit eines Fehlers vom Typ I, sodass der familienbezogene Typ-I-Fehler die Wahrscheinlichkeit ist, dass mindestens einer dieser Vergleiche zu einem Fehler vom Typ I führt.Wenn viele Vergleiche durchgeführt werden, wird die familienbezogene Wahrscheinlichkeit eines Fehlers vom Typ I stark aufgeblasen

Eine Einweg-ANOVA ist so konzipiert, dass sie zwei oder mehr Beispiele vergleichen. Wenn Sie jedoch zwei Beispiele vergleichen möchten, ist es möglicherweise effizienter, direkt unsere zu verwenden T-Test für Zwei Unabhängige Probe .

Nicht parametrische alternativen zu anova

ANOVA verlangt bestimmte Annahmen, nämlich Normalität und Homogenität von Abweichungen zu halten.Es ist bekannt, dass ANOVA relativ robust gegen Verstöße gegen die Annahmen ist, insbesondere wenn sie mild sind.Aber was tun, wenn die Annahmen einfach nicht erfüllt sind?

In diesem Fall können Sie unsere verwenden Kruskal-Wallis-Testrechner , das ist das nicht parametrische Äquivalent zu ANOVA.Ein Vorteil des Kruskal-Wallis-Tests besteht darin, dass Sie ihn auch mit Ordnungsdaten verwenden können, für die die Verwendung von ANOVA keine gute Idee wäre.