Teste de linha horizontal

Esta calculadora permitirá que você execute o teste de linha horizontal para qualquer função fornecida, mostrando as etapas. A função que você fornece poderia ser algo como 'y = 2x - 1', que é o tipo mais simples de Função linear você pode encontrar ou pode fornecer uma função mais complexa como 'y = (2x-1)/(x+1)' que envolve um função racional .

Depois de fornecer uma função válida, você pode clicar no botão “Calcular” e serão fornecidas todas as etapas do processo, indicando se a função passa ou não no teste de linha horizontal (HLT).

A maneira como esta calculadora funciona é definindo uma linha horizontal genérica e verificando quantas vezes (se é que alguma vez) a linha cruza essa linha horizontal arbitrária. Isso envolve Resolvendo para x a equação y = f(x).

O que é o teste da linha horizontal?

O HLT é um teste que permite avaliar se uma função é injetora ou não. Consiste em desenhar linhas horizontais em diferentes alturas e ver onde elas cruzam o gráfico da função dada f(x), se é que o fazem.

Se nenhuma linha horizontal que você possa imaginar cruzará o gráfico da função f(x) mais de uma vez, então a função é um para um . Por outro lado, se você conseguir encontrar uma reta horizontal que cruze o gráfico da função f(x) MAIS DE UMA VEZ, então você provou que a função NÃO é injetiva

Então você pode estar pensando "Espere um minuto", esta ferramenta não funciona realmente para provar que uma função é injetiva usando o teste da linha horizontal, mas sim para provar que NÃO É injetiva usando-a .

Porque, em termos práticos, não posso representar graficamente TODAS as retas horizontais que existem para verificar quantas vezes elas cruzam o gráfico de f(x), mas se eu encontrar UMA reta horizontal que cruze o gráfico de f(x) muitas vezes, então eu sei que não é um para um. Então, pensando bem, você está no caminho certo.

Usando o teste da linha horizontal na praticidade

Por exemplo, se você tiver a função $f(x) = x^2$, o gráfico seria mais ou menos parecido com:

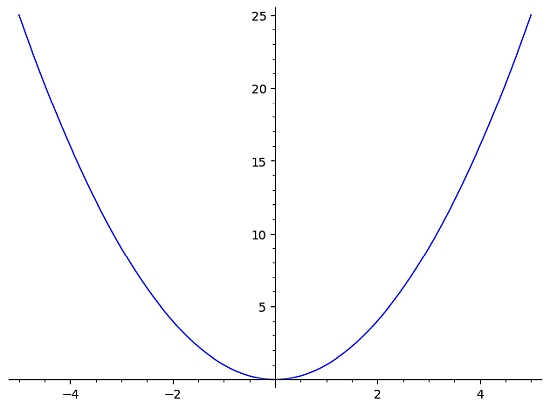
Neste caso, vemos imediatamente que esta função falha no teste da linha horizontal. Por que, porque a reta horizontal y = 10 mostrada no gráfico abaixo cruza o gráfico de f(x) duas vezes (mais de uma vez)

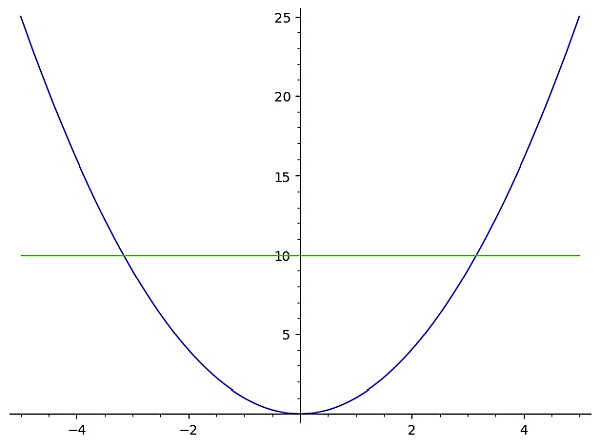
Neste caso, a função $f(x) = x^2$ falha no teste da linha horizontal e, portanto, não é uma função função um para um .

Agora, como é impossível testar TODAS as linhas horizontais possíveis, o HLT precisa ser tentado usando meios algébricos, a menos que você veja visualmente um caso claro de uma linha horizontal que fará com que a função falhe no teste.

Usando o teste de linha horizontal (analiticamente)

• Passo 1: Comece com uma determinada função válida f(x), você definirá o nível de uma linha horizontal em um valor arbitrário de y
• Passo 2: Então você define a equação: y = f(x), e o objetivo é resolver x
• Etapa 3: Não existe uma estratégia resolva esta equação , pois depende da natureza da função f(x). Se f(x) for uma função linear ou quadrática simples, então é muito fácil resolver x. Caso contrário, diferentes métodos precisam ser testados
• Passo 4: Se ao resolver x você encontrar mais de uma solução para um y arbitrário, a função falhará no HLT. Caso contrário, se houver uma solução ou nenhuma solução, ela será aprovada.

A subtração de frações é derivada apenas pela soma de frações: Para subtrair duas frações, basta multiplicar a segunda por -1 e adicioná-la à primeira .

A linha horizontal pode assumir valores negativos ou positivos?

A chave principal da implementação analítica do HLT é escolher uma linha horizontal arbitrária. Pode ser um valor arbitrário, positivo ou negativo. Então, o valor arbitrário de y usado PODE determinar se as soluções propostas estão bem definidas ou não, mas isso não ADICIONA mais soluções, mas pode potencialmente subtrair soluções.

Por exemplo, quando você começa com $f(x)= \frac{2x+1}{x-1}$ e resolve para x isto: $y = \frac{2x+1}{x-1}$, você chegará a

$x = \frac{y+1}{y-2}$

o que significa que para um determinado $y$ você tem NO MÁXIMO uma solução. Por que uma solução no máximo? Porque quando y = 2 na verdade não há solução, e para qualquer outro y, há uma solução. Isso funciona muito bem para mostrar que a função passa no teste da linha horizontal.

Exemplo: passar no hlt

A função a seguir passa no HLT: $f(x) = \frac{1}{3} x + \frac{5}{4}$ ?

Solução:

A função fornecida é:

$$f\left(x\right) = \frac13x+\frac54$$

Então, para avaliar se a função dada passa ou não no Teste da Reta Horizontal, precisamos resolver $x$ e determinar se não há solução, uma solução ou múltiplas soluções. A equação inicial é

$$y=\frac{1}{3}x+\frac{5}{4}$$

Resolvendo a equação linear

Colocando $x$ no lado esquerdo e $y$ e a constante no lado direito obtemos

$$\displaystyle -\frac{1}{3}x = -y -\left(-\frac{5}{4}\right)$$

Agora, resolvendo para $x$, dividindo ambos os lados da equação por $-\frac{1}{3}$, obtém-se o seguinte

$$\displaystyle x=-\frac{1}{-\frac{1}{3}}y+\frac{\frac{5}{4}}{-\frac{1}{3}}$$

e simplificando, finalmente obtemos o seguinte

$$\displaystyle x=3y-\frac{15}{4}$$

Portanto, a resolução de $x$ para determinada equação linear leva a $x = 3y-\frac{15}{4}$.

Descobrimos que, como ao resolver $x$ encontramos uma solução e é apenas uma solução, a função dada passa no Teste da Linha Horizontal.

Os resultados do teste de linha horizontal

Com base no trabalho mostrado acima, pode-se concluir que a função dada passa no Teste da Linha Horizontal.

Graficamente, a situação é representada da seguinte forma:

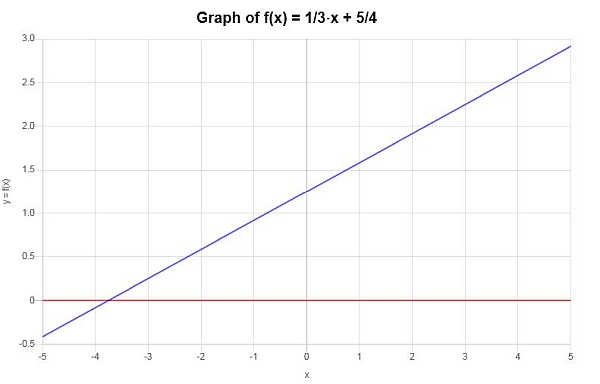
Exemplo: esta função é um para um?

Usando o teste da linha horizontal, indique se a seguinte função é injetora: $f(x) = x^3 - 1$

Solução: Para avaliar se a função dada passa ou não no Teste da Reta Horizontal, precisamos resolver a equação $y = x^3 - 1$ para $x$ e determinar se não há solução, uma solução ou múltiplas soluções.

Etapa Inicial: Neste caso, primeiro precisamos simplificar a equação dada e, para isso, realizamos as seguintes etapas de simplificação:

Então, obtemos as soluções:

$$x_1=\left(y+1\right)^{\frac{1}{3}}$$ $$x_2=\frac{1}{2}\left(y+1\right)^{\frac{1}{3}}\left(i\sqrt{3}-1\right)$$ $$x_3=-\frac{1}{2}\left(y+1\right)^{\frac{1}{3}}\left(i\sqrt{3}+1\right)$$

Destas soluções, temos apenas uma solução real, que é $x_1=\left(y+1\right)^{\frac{1}{3}}$. Portanto, e como ao resolver $x$ encontramos uma solução e é apenas uma solução real, a função dada passa no Teste da Reta Horizontal.