Mais sobre funções lineares

Esta calculadora de função linear permitirá que você calcule uma Função linear fornecendo certas informações necessárias sobre a função.

Existem várias maneiras de fazer isso. Você pode (1) fornecer uma equação linear em x e y que pode ser resolvida para y ou (2) fornecer diretamente a declive e Y-Intercept , ou (3) você pode fornecer a inclinação e um ponto por onde a linha passa, ou (4) você pode fornecer 2 pontos por onde a linha passa.

Quais informações você fornecerá? Depende muito de quais informações você tem disponível e dependerá do caso específico.

Um caso comum é encontrar uma função linear que passa por dois pontos dados, mas as outras formas de determinar a linha também são comuns.

O que é uma função linear?

A resposta depende de quantas variáveis você está considerando, mas para uma variável x, uma função linear é uma função da forma

$$f(x) = a + b x$$

Apenas um detalhe técnico, em matemática mais avançada, esta é uma função afim linear, e não é estritamente linear a menos que a = 0, mas essa ideia vai além do escopo desta apresentação. Para nós, $f(x) = a + b x$ é uma função linear em x.

O valor de a em $f(x) = a + b x$ é conhecido como Y-Intercept , e b é conhecido como declive . Algumas vezes você verá a convenção $f(x) = mx + n$, onde m é a inclinação e n é a interceptação y.

Mas isso é uma convenção de nomes, você só precisa lembrar que a constante que multiplica a variável x é a inclinação e a outra é a interceptação y. Por que é que? Porque quando x = 0, obtemos $f(0) = m \cdot 0 + n = n$, o que indica que n é precisamente a interceptação por que.

Quais são as etapas para calcular uma função linear?

• Passo 1: Identifique o tipo de informação que você forneceu
• Passo 2: Se a informação que você tem é uma equação linear em x e y, você precisa resolver para y e então você automaticamente tem a configuração da função linear f(x) = y
• Etapa 3: se você tiver a inclinação b e a interceptação y a, a função linear será diretamente f(x) = a + b x
• Passo 5: Se você tem dois pontos $(x_1, y_1)$ e $(x_2, y_2)$ onde a linha passa, então você pode usar a fórmula: $\displaystyle f(x) = y_1 + \left(\frac{y_2-y_1}{x_2-x_1} \right)(x-x_1)$ para a função linear
• Etapa 6: Se, em vez disso, você tiver um ponto $(x_1, y_1)$ por onde passa a linha e a inclinação, poderá usar a fórmula: $\displaystyle f(x) = y_1 + m(x-x_1)$ para a função linear

A lista de etapas acima é uma lista abrangente e considera todos os casos possíveis. Ultimate, a situação mais simples e menos complicada corresponde ao caso em que a inclinação e a interceptação y são conhecidas, onde podemos calcular o formulário de intercepção de encostas imediatamente, mas nem sempre é assim.

Qual é a fórmula da função linear

Por fim, e independentemente das informações que você forneceu, você pode chegar à fórmula da função linear conhecida como forma de interceptação da inclinação, que é:

$$y = a + bx$$

Agora, como você está definindo uma função, você também pode escrever $f(x) = a + b x$.

Quais são as etapas para encontrar a fórmula da função linear?

• Passo 1: Identifique as informações fornecidas
• Etapa 2: chegar à fórmula correspondente y = a + bx, identificando a inclinação b e a interceptação y a
• Passo 3: Substitua y por f(x) e escreva f(x) = a + bx

Geometricamente, o gráfico de função linear será uma linha que realmente cruza o eixo y no ponto (0, a), e a inclinação b refletirá o grau de inclinação da linha.

Por que é útil calcular funções lineares?

A relação linear entre variáveis é muito comum em tantas aplicações, por isso torna-se indispensável entender completamente como as funções lineares funcionam.

E também podemos definir funções lineares para mais variáveis, o que as torna um objeto ainda mais poderoso.

Exemplo: calculadora de função linear

Calcule a equação da função linear que passa pelos pontos: $(\frac{22}{3}, \frac{7}{4})$ e $(-1, \frac{5}{6})$

Solução: O objetivo principal é construir uma função linear com base nas informações fornecidas, se possível.

A informação fornecida sobre a linha é que a linha passa através dos pontos$\displaystyle \left( \frac{22}{3}, \frac{7}{4}\right)$ e $\displaystyle \left( -1, \frac{5}{6}\right)$>>

Por conseguinte, o primeiro passo consiste em calcular a inclinação. A fórmula para o declive é: $$\displaystyle b = \frac{y_2 - y_1}{x_2 - x_1}$$

Agora, ao ligar os números correspondentes é , obtemos que a inclinação é: $$\displaystyle b = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ \displaystyle \frac{5}{6} - \frac{7}{4}}{ \displaystyle -1 - \frac{22}{3}} = \frac{ \displaystyle \frac{5}{6}-\frac{7}{4}}{ \displaystyle -1-\frac{22}{3}} = \frac{11}{100}$$

Então, agora sabemos que a inclinação é $\displaystyle m = \frac{11}{100}$ e que a linha passa pelo ponto $\displaystyle \left( \frac{22}{3}, \frac{7}{4}\right)$>

Assim, com a informação de que dispomos, podemos construir directamente a forma pontiaguda da linha, que é

$$\displaystyle y - y_1 = b \left(x - x_1\right)$$>>

e depois ligando os valores conhecidos de <$\displaystyle b = \frac{11}{100}$ e $\displaystyle \left( x_1, y_1 \right) = \left( \frac{22}{3}, \frac{7}{4}\right)$, obtemos que

$$\displaystyle y-\frac{7}{4} = \frac{11}{100} \left(x-\frac{22}{3}\right)$$>>

Agora, precisamos de expandir o lado direito da equação, distribuindo a inclinação, de modo a obter $$\displaystyle y = \frac{11}{100} x + \frac{11}{100} \left(-\frac{22}{3}\right) + \frac{7}{4}$$>

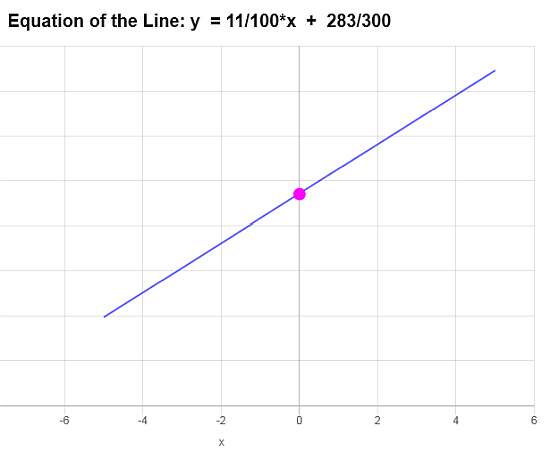
e simplificando, vamos obter que <$$\displaystyle y=\frac{11}{100}x+\frac{283}{300}$$>>>

Conclusão : Com base nos dados fornecidos, concluímos que a equação da reta é $\displaystyle f(x)=\frac{11}{100}x+\frac{283}{300}$ e corresponde a uma reta com uma inclinação de $\displaystyle b = \frac{11}{100}$ e interceptação y de $\displaystyle a = \frac{283}{300}$.

Com base nessas informações, o gráfico é:

Exemplo: outro cálculo de função linear

Calcule a função linear associada a: $\frac{1}{3}x + \frac{5}{4}y - \frac{5}{6} = 0$

Solução:

Agora, para este exemplo, a maneira como definimos uma função linear é por meio de uma equação linear geral, dada por:

$$\displaystyle \frac{1}{3}x+\frac{5}{4}y-\frac{5}{6}=0$$>>

Podemos simplificar constantes:

$$\displaystyle \frac{1}{3}x+\frac{5}{4}y-\frac{5}{6}=0$$>>

Agora, colocando $y$ no lado esquerdo e $x$ e a constante no lado direito, obtemos

$$\displaystyle \frac{5}{4}y = -\frac{1}{3}x + \frac{5}{6}$$>>

Agora, resolvendo para $y$, dividindo ambos os lados da equação por $\frac{5}{4}$, obtém-se o seguinte

$$\displaystyle y=-\frac{\frac{1}{3}}{\frac{5}{4}}x+\frac{\frac{5}{6}}{\frac{5}{4}}$$>>

e simplificando, finalmente obtemos o seguinte

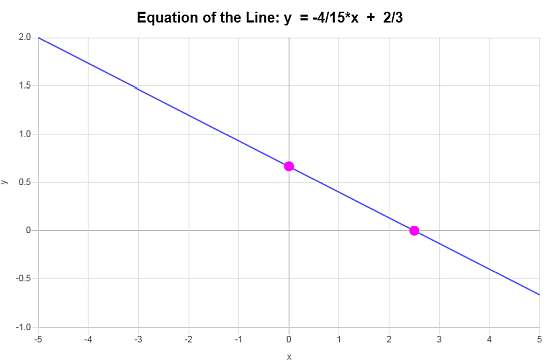
$$\displaystyle y=-\frac{4}{15}x+\frac{2}{3}$$>>

Conclusão : Agora podemos dizer que com base nos dados fornecidos, a conclusão é que a equação da reta é $\displaystyle f(x)=-\frac{4}{15}x+\frac{2}{3}$, e corresponde a uma reta com uma inclinação de $\displaystyle b = -\frac{4}{15}$ e interceptação y de < >.

Com base nessas informações, o gráfico é:

Exemplo: mais calculadoras de funções lineares

Calcule a função linear com inclinação m = 0 e que cruza o eixo y no ponto (0, 4).

Solução: Nesse caso, fornecemos a inclinação, que é m = 0, e a interceptação y, que é (0, 4). Como a inclinação é 0, a reta é horizontal, portanto, neste caso, a equação da reta é $f(x) = 4$.

Mais calculadoras de funções lineares

Calculadoras interessantes são a calculadora de inclinação e a calculadora de interceptação y. Também você pode estar interessado em encontrar a linha perpendicular a uma linha dada .

Outra forma comum para a linha é a formulário padrão , e você pode converter de uma forma para outra.