Solventes Álgebra

Gráfico de funções

Instruções: Use esta calculadora de gráfico de função para gerar o gráfico de uma função que você fornece. Por favor, digite qualquer função válida que você deseja representar graficamente na caixa de formulário abaixo.

Gráfico de funções

Esta calculadora de gráfico de função permitirá que você gere o gráfico de qualquer função que você fornecer. Você precisa fornecer uma função válida em x.

Pode ser uma função que já está simplificada, como f(x) = sin(2x), ou pode ser algo mais complexo como 'f(x) = sin((1/3 x +1/4 x^2) (1/5 x +1/6))', e esta calculadora fará o simplificação de função para voce.

Depois de digitar uma função válida no formulário correspondente, basta clicar em 'Calcular' para obter o gráfico gerado.

Trabalhando com o gráfico de uma função pode ajudá-lo a entender suas principais propriedades. Com efeito, tendo o gráfico de funções pode dizer tudo o que você precisa sobre o comportamento da função: ela está aumentando? Está diminuindo? Ele cruza o eixo x? Tem algum tipo de simetria?

Qual é o gráfico da função?

O gráfico da função para uma dada função f(x) é o conjunto de pontos (x, f(x)). Isso, quando desenhado nos eixos x-y, parece uma 'curva' (pode ser uma linha) que flui da esquerda para a direita.

Agora, esse fluxo da esquerda para a direita tem uma propriedade bem específica: ele passa no teste da reta vertical, que indica que o gráfico de uma função, quando interceptado por qualquer reta vertical, terá no máximo um ponto de interseção. Por exemplo, o gráfico abaixo corresponde a um gráfico de função porque passa no teste da linha vertical.

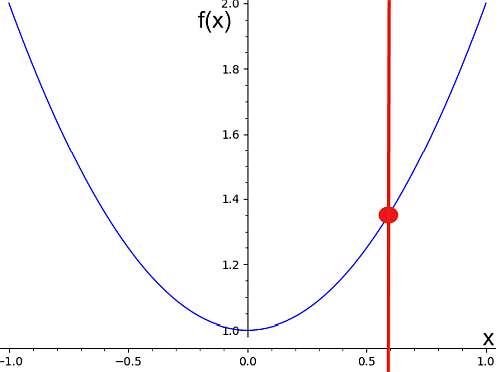
Por outro lado, o gráfico abaixo não corresponde ao gráfico de uma função, pois podemos ver uma reta vertical que cruza a curva em dois pontos.

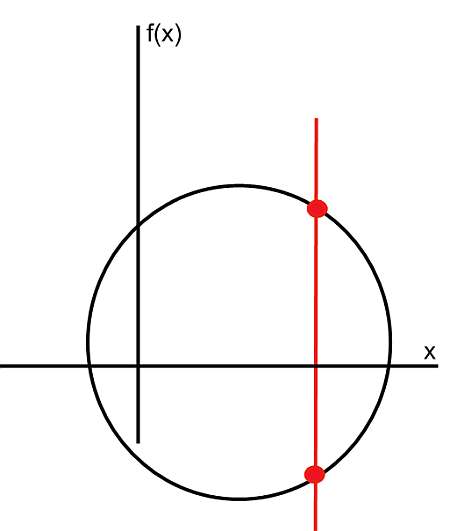
Quais são os passos para encontrar o gráfico da função?

Passo 1: Identifique a função que deseja representar graficamente. Por inspeção, avalie se a função é válida ou não
Passo 2: Se a função for uma expressão válida, encontre pontos potenciais onde a função não pode ser avaliada (divisões por zero ou raízes quadradas de números negativos)
Passo 3: Simplifique o máximo que puder, para coloque a função em sua forma mais simples
Passo 4: Tente identificar padrões conhecidos. A função em sua forma mais simples é um polinômio? Os polinômios têm uma forma específica. A função é uma função trigonométrica? Eles também têm uma forma muito conhecida e característica
Etapa 5: Se você não tiver nenhum padrão simples e reconhecível ou função conhecida, crie uma tabela de pontos (x, f(x)), tantos pontos quanto for prático
Etapa 6: plote esses pontos de sua tabela no plano XY. Trace uma curva através desses pontos para ter uma ideia de como o gráfico da função se parece

Simplificando a função à sua forma mais simples irá ajudá-lo a identificar de forma mais fácil quaisquer funções conhecidas que aparecem e podem ser facilmente representadas graficamente.

Como representar graficamente funções conhecidas?

Quando simplificando uma função , não espere ter diretamente coisas muito simples como \(f(x) = x^2\) (uma parábola simples) ou \(f(x) = x\) (uma linha simples), mas você pode ter traduções de versões em escala dessas básicas. Com efeito, por exemplo, qualquer função quadrática pode ser colocado em Vertex Form , que ajuda a identificar a curva como uma parábola simples que é transladada.

Quais são as etapas para fazer transformações de gráfico de função?

Etapa 1: Identifique a função que deseja representar graficamente
Passo 2: Simplifique o máximo que puder evitando a armadilha de dividindo por zero e tirando a raiz quadrada de valores negativos
Passo 3: Com a versão mais simples da função, veja se alguma função elementar pode ser reconhecida
Passo 4: Se não, veja se alguma transformação de funções comuns (polinômios, retas, funções trigonométricas , etc) podem ser identificados, pois também são fáceis de representar graficamente
Etapa 5: Se tudo acima falhar, basta construir uma tabela com valores (x, f(x)) e traçar manualmente a forma do gráfico

Claro que você não precisa fazer o gráfico manualmente, você pode usar isso gráfico de função on-line ferramenta para obter um gráfico preciso e elegante.

Por que você gostaria de saber sobre os tipos de gráficos de funções?

O gráfico de uma função pode basicamente dizer tudo sobre a função. Até certo ponto, o gráfico da função é o função , ou pelo menos uma representação dele.

Existe uma correspondência entre função e gráfico, o que indica que o gráfico basicamente informa tudo o que você precisa saber sobre a função.

Exemplo: encontrar o gráfico da função

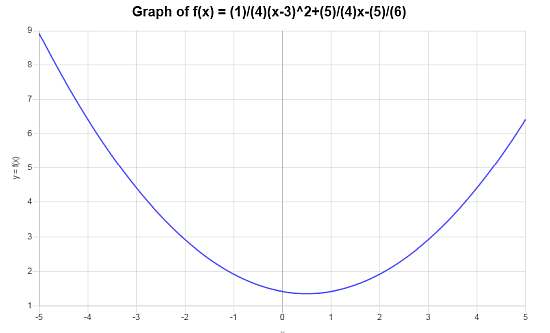
Calcule o gráfico de função do seguinte: \(f(x) = \frac{1}{4}(x-3)^2 + \frac{5}{4} x - \frac{5}{6}\)

Solução: A seguinte função foi fornecida \(\displaystyle f(x) = \frac{1}{4}\left(x-3\right)^2+\frac{5}{4}x-\frac{5}{6}\) para a qual precisamos construir seu gráfico.

Passo 0: Nesse caso, primeiro precisamos simplificar a função dada \(\displaystyle f(x) = \frac{1}{4}\left(x-3\right)^2+\frac{5}{4}x-\frac{5}{6} \) e, para isso, realizamos as seguintes etapas de simplificação:

\( \displaystyle \frac{1}{4}\left(x-3\right)^2+\frac{5}{4}x-\frac{5}{6}\)

By distributing the terms inside of the parentheses

\( = \,\,\)

\(\displaystyle \frac{1}{4}\left(x^2-3x-3x+3^2\right)+\frac{5}{4}x-\frac{5}{6}\)

Evaluating the exponential: \(3^2 = 9\)

\( = \,\,\)

\(\displaystyle \frac{1}{4}\left(x^2-3x-3x+9\right)+\frac{5}{4}x-\frac{5}{6}\)

Putting together the terms with \(x\)

\( = \,\,\)

\(\displaystyle \frac{1}{4}\left(x^2+\left(-3-3\right)x+9\right)+\frac{5}{4}x-\frac{5}{6}\)

Putting together numerical values and fractions and operating the terms that were grouped with \(x\)

\( = \,\,\)

\(\displaystyle \frac{1}{4}\left(x^2-6x+9\right)+\frac{5}{4}x-\frac{5}{6}\)

We distribute the terms inside of the parentheses

\( = \,\,\)

\(\displaystyle \frac{1}{4}x^2-\frac{1}{4}\cdot 6x+9\cdot \frac{1}{4}+\frac{5}{4}x-\frac{5}{6}\)

Grouping and operating all the integer terms and fractions: \(\displaystyle 9 \times \frac{ 1}{ 4}=\frac{ 9}{ 4}\)

\( = \,\,\)

\(\displaystyle \frac{1}{4}x^2+6-\frac{ 1}{ 4}x+\frac{9}{4}+\frac{5}{4}x-\frac{5}{6}\)

Grouping and operating all the integer terms and fractions: \(\displaystyle \frac{ 9}{ 4}-\frac{ 5}{ 6}=\frac{ 9}{ 4} \times \frac{ 3}{ 3}-\frac{ 5}{ 6} \times \frac{ 2}{ 2}=\frac{ 9 \times 3-5 \times 2}{ 12}=\frac{ 27-10}{ 12}=\frac{ 17}{ 12}\)

\( = \,\,\)

\(\displaystyle \frac{1}{4}x^2-\frac{1}{4}x+\frac{17}{12}\)

O seguinte gráfico é obtido para a função simplificada \(\displaystyle f(x)=\frac{1}{4}x^2-\frac{1}{4}x+\frac{17}{12}\) no intervalo \([-5, 5]\):

Exemplo: regras do gráfico de função

Calcule o gráfico para a função \(f(x) = \frac{1}{3}(x-4)^2 - \frac{5}{6}\). Esta função é uma transformação de gráfico de função de uma função básica e bem conhecida?

Solução: Expandindo e simplificando a função:

\( \displaystyle \frac{1}{3}\left(x-4\right)^2-\frac{5}{6}\)

We distribute the terms inside of the parentheses

\( = \,\,\)

\(\displaystyle \frac{1}{3}\left(x^2-4x-4x+4^2\right)-\frac{5}{6}\)

Evaluating the exponential: \(4^2 = 16\)

\( = \,\,\)

\(\displaystyle \frac{1}{3}\left(x^2-4x-4x+16\right)-\frac{5}{6}\)

Aggregating those terms with \(x\)

\( = \,\,\)

\(\displaystyle \frac{1}{3}\left(x^2+\left(-4-4\right)x+16\right)-\frac{5}{6}\)

Putting the integers together and operating the terms that were grouped with \(x\)

\( = \,\,\)

\(\displaystyle \frac{1}{3}\left(x^2-8x+16\right)-\frac{5}{6}\)

We need to distribute the terms inside of the parentheses

\( = \,\,\)

\(\displaystyle \frac{1}{3}x^2-\frac{1}{3}\cdot 8x+16\cdot \frac{1}{3}-\frac{5}{6}\)

Grouping and operating all the integer terms and fractions: \(\displaystyle 16 \times \frac{ 1}{ 3}=\frac{ 16}{ 3}\)

\( = \,\,\)

\(\displaystyle \frac{1}{3}x^2+8-\frac{ 1}{ 3}x+\frac{16}{3}-\frac{5}{6}\)

Grouping and operating all the integer terms and fractions: \(\displaystyle \frac{ 16}{ 3}-\frac{ 5}{ 6}=\frac{ 16}{ 3} \times \frac{ 2}{ 2}-\frac{ 5}{ 6}=\frac{ 16 \times 2-5}{ 6}=\frac{ 32-5}{ 6}=\frac{ 27}{ 6}=\frac{ 3 \times 9}{ 3 \times 2}=\frac{ \cancel{ 3} \times 9}{ \cancel{ 3} \times 2}=\frac{ 9}{ 2}\)

\( = \,\,\)

\(\displaystyle \frac{1}{3}x^2-\frac{8}{3}x+\frac{9}{2}\)

O seguinte gráfico é obtido para \(\displaystyle f(x)=\frac{1}{3}x^2-\frac{8}{3}x+\frac{9}{2}\) no intervalo \([-10, 10]\):

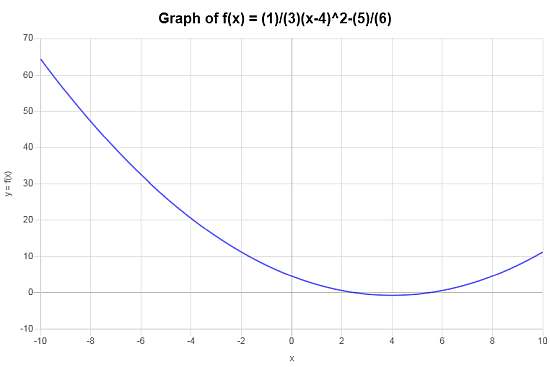
Neste caso, o gráfico é \(f(x) = \frac{1}{3}(x-4)^2 - \frac{5}{6}\) de fato a transformação do simples \(g(x) = x^2\), que foi deslocado para a esquerda em 4 unidades, deslocado para baixo em \(\frac{5}{6}\) e redimensionado.

Exemplo: outro exemplo de gráfico de função

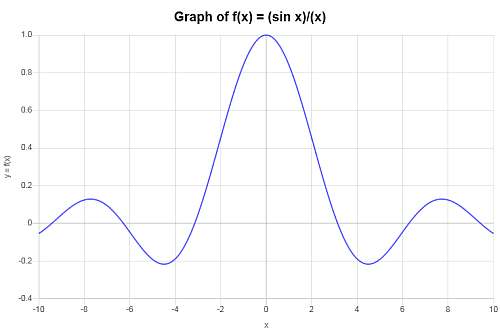
Calcule o gráfico de \( f(x) = \displaystyle \frac{\sin(x)}{x}\).

Solução: A seguinte função foi fornecida: \(\displaystyle f(x) = \frac{\sin\left(x\right)}{x}\), então o seguinte gráfico é obtido, intervalo \([-10, 10]\):

Outras calculadoras de funções

Dada uma função que você deseja ser capaz de simplifique a função , para colocá-lo em sua forma mais simples. Já vimos que é benéfico identificar de forma mais fácil a potencial transformação do gráfico de funções a partir de funções básicas que podem estar ali.