Funções individuais
Instruções: Use esta calculadora para testar uma função um-para-um, mostrando todas as etapas. Digite a função que deseja verificar na caixa abaixo.
Funções individuais
Esta calculadora permitirá avaliar se uma função é biunívoca ou não, mostrando todos os passos. A primeira coisa que você precisa fazer é fornecer a função. Isso pode ser algo simples, linear ou quadrático como 'y = x^2 - 1', ou você pode decidir optar por um função racional como 'f(x) = (x-1)/(x+3)'.
Então, você está satisfeito com o que forneceu e se certificou de que a função é válida, clique no botão "Calcular", para obter todas as etapas do processo que lhe são mostradas.
O conceito de função injetora é muito importante em Álgebra e Cálculo. Existem muitas maneiras simples de testar um para um, uma delas é a Teste de linha horizontal , mas devido à sua natureza, é mais fácil de usar para refutar que uma função é injetora. Para provar que uma função é injetiva, precisamos de um resolução de equações , processo analítico.

O que é um processo um-para-um
Simplificando, uma função um-para-um ou injetiva é aquela que para dois \(x_1\) e \(x_2\) diferentes, os valores de suas imagens através de \(f(x)\) são diferentes, o que significa matematicamente
\[\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \]Alguns instrutores gostam de escrevê-la de maneira um pouco diferente, mas ainda de forma equivalente: A função é injetora se
\[\displaystyle f(x_1) = f(x_2) \Rightarrow x_1 = x_2 \]Isto quer dizer de uma forma bastante sofisticada que, se o gráfico da função cruzar o mesmo valor (uma linha horizontal), isso só acontecerá quando o ponto for o mesmo. Então, tudo o que você está dizendo é que não existem dois pontos diferentes onde uma linha horizontal o cruza. Então, você está apenas reiterando o Teste de linha horizontal .
Como verificar se uma função é injetora ou não
- Passo 1: Comece com a função original f(x) e defina a equação y = f(x)
- Passo 2: Tente resolver para x
- Etapa 3: Se você encontrar mais de uma solução, então a função NÃO é injetiva, e se tiver uma solução ou nenhuma solução, então a função é injetiva
Normalmente, você fará algumas inspeções básicas para ter certeza de que essa função claramente não é um-para-um, possivelmente porque você pode facilmente encontrar uma linha horizontal para fazer o HLT falhar.
A seguir, você procurará algumas propriedades visuais básicas: A função está sempre aumentando (então é bijetora), e o mesmo vale para o caso em que a função está sempre diminuindo.
Como um para um está relacionado com encontrar o inverso
Dito em termos simples, para encontrar a inversa de uma função, a função DEVE ser bijetora, pelo menos em um determinado subdomínio. Muitas vezes restringimos o domínio, então criamos uma função 1 para 1 em um domínio restrito, que de outra forma não seria 1 para 1.
Por exemplo, \(f(x) = x^2\) não é um para um no geral. Porque você pode pegar dois pontos diferentes \(x_1 = -1\) e \(x_2 = 1\) e descobrir que \(f(x_1) = (-1)^2 = 1\) e \(f(1) = 1^2 = 1\), o que significa que a propriedade (a caracterização um-para-um)
\[\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \]não está satisfeito. Agora, se em vez de considerarmos a linha real completa \(\R\), considerarmos apenas os valores positivos, podemos concluir que a função é bijetora nos valores reais positivos (Dica: Nesse subdomínio, a função é crescente)

Existe uma fórmula para avaliar se uma função é injetora?
Infelizmente não. Quero dizer, pode-se pensar em \(\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \) como uma fórmula um-para-um, mas esta é mais uma condição lógica do que uma fórmula.
Porém, existe um procedimento genérico muito amplo que é usado para testar se uma função é injetora ou não, que é o que você vê explicado acima. Não existe uma “fórmula um-para-um”. Se precisássemos nos contentar com um, deveria ser y = f(x).
E, acabamos de resolver para x. Nada mais nada menos. Em última análise, vai depender do que se trata f(x). Uma função muito complexa e complicada pode apresentar muitas dificuldades para ser resolvida, e talvez você precise de uma calculadora de funções para ela, e mesmo com uma calculadora de funções você pode falhar.
Você provavelmente está pensando, por que isso? É porque, no fundo, não temos técnicas para resolver TODAS as equações. Apenas fazemos o que podemos com alguns tipos específicos de equações, mas estamos longe de saber uma maneira EXATA de resolver todas as equações.

Exemplo: função um para um
A seguinte função é injetiva: \(f(x) = \frac{1}{4} x + \frac{5}{4}\)
Solução:
Recebemos a seguinte função:
\[f(x) = \frac{1}{4} x + \frac{5}{4}\]Então, para avaliar se a função dada é injetiva ou não, precisamos resolver \(x\) e determinar se não há solução, uma solução ou múltiplas soluções. A equação inicial é
\[y=\frac{1}{4}x+\frac{5}{4}\]Colocando \(x\) no lado esquerdo e \(y\) e a constante no lado direito obtemos
\[\displaystyle -\frac{1}{4}x = -y -\left(-\frac{5}{4}\right)\]Agora, resolvendo para \(x\), dividindo ambos os lados da equação por \(-\frac{1}{4}\), obtém-se o seguinte
\[\displaystyle x=-\frac{1}{-\frac{1}{4}}y+\frac{\frac{5}{4}}{-\frac{1}{4}}\]e simplificando, finalmente obtemos o seguinte
\[\displaystyle x=4y-5\]Portanto, a resolução de \(x\) para determinada equação linear leva a \(x=4y-5\) e é apenas uma solução real, então a função dada é bijetora.
Conclusão
Com base no que foi encontrado na seção anterior, pode-se concluir que a função dada é bijetora.
Graficamente:
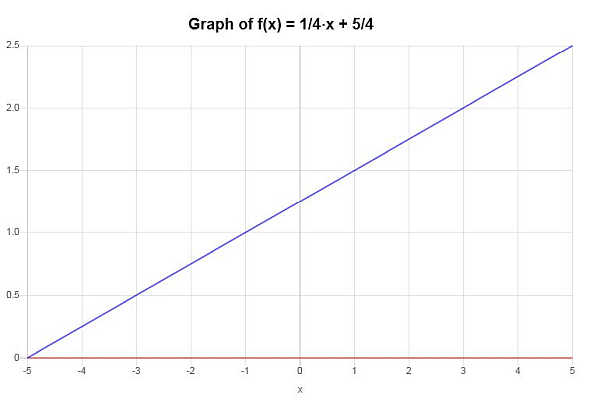
Exemplo: função 1 para 1
Prove ou refute que a seguinte função é injetora: \(f(x) = \frac{1}{3} x^2 - 5x - \frac{5}{6}\)
Solução: Para avaliar se a função dada é injetiva ou não, precisamos resolver \(x\) e determinar se não há solução, uma solução ou múltiplas soluções. A equação inicial que precisamos usar é:
\[y=\frac{1}{3}x^2-5x-\frac{5}{6}\]Etapa Inicial: Neste caso, primeiro precisamos simplificar a equação dada e, para isso, realizamos as seguintes etapas de simplificação:
Então, as soluções são:
\[x_1=-\frac{1}{2}\sqrt{12y+235}+\frac{15}{2} \] \[x_2=\frac{1}{2}\sqrt{12y+235}+\frac{15}{2} \]Status individual
Com base no trabalho mostrado acima, pode-se concluir que a função dada NÃO É UM PARA UM, pois não passa no Teste da Linha Horizontal, como por exemplo a linha \(y = 0\) é uma linha horizontal que cruza a função dada mais de uma vez.
Graficamente, a situação é representada da seguinte forma:
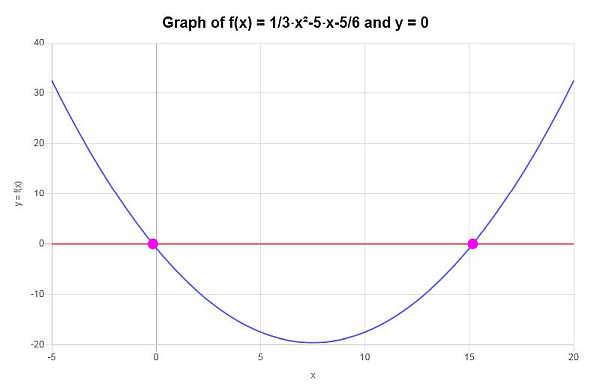
Calculadoras de álgebra mais interessantes
O conceito de funções 1 para 1 geralmente é dado como certo, mas é muito importante, crítico, eu diria. Isso ocorre porque o conceito de um para um está intimamente ligado à ideia de função monótona (funções crescentes ou decrescentes), ao mesmo tempo que está intimamente relacionado com o cálculo da função inversa e seu gráfico.
No entanto, muitas vezes é difícil passar da floresta pelas árvores, já que os conceitos mais cruciais de Álgebra e Cálculo têm ligações estreitas entre si. Análise de função é uma das coisas que você fará o tempo todo, então é bom adquirir as habilidades para se tornar bom nisso.






