Calculadora de função inversa
Instruções: Use esta calculadora para encontrar a função inversa de uma função que você fornece, mostrando todas as etapas. Por favor, digite a expressão da função para a qual deseja encontrar o inverso na caixa abaixo.
Mais sobre esta calculadora de função inversa
Esta calculadora permitirá que você encontre o inverso de uma determinada função mostrando todas as etapas, assumindo que o inverso existe. A calculadora examinará a função resolver uma equação associado à definição da função, e tentará avaliar se existe ou não uma inversa.
Por exemplo, você pode fornecer uma função linear como 'f(x) = 3x - 2', que seria um caso simples, ou, por exemplo, você poderia aumentar um pouco com algo um pouco mais difícil, como uma função racional como 'y = (x-1)/(x-3)'.
Depois de fornecer uma função válida, clique no botão "Calcular" para obter todas as etapas do processo mostradas a você, com a função inversa como resposta final, se existir uma inversa, ou com a explicação de que nenhuma solução foi encontrada e porque.
Não é garantido que você encontrará todas as funções inversas. Por um lado, nem todas as funções têm uma inversa e, por outro lado (como veremos na próxima seção), o processo de encontrar a inversa envolve Resolvendo para x para uma equação e, como sabemos, algumas equações podem ser muito difíceis ou impossíveis de resolver.
Portanto, é mais provável que funções mais simples sejam capazes de encontrar seu inverso, caso o inverso exista.

Como você define o inverso de uma função?
Em termos leigos, o inverso de uma função é a função que faz o oposto do que a função original faz. Então, pense em uma função em termos de y = f(x), e então você poderia pensar nela ao passar de x para y. Você alimenta a função com um x, e a função fornece um y específico.
A função inversa começa com y e encontra o caminho de volta para x, de forma que x seja o mesmo que levou a y através da função original. Agora, a definição formal é feita via composição de função . Para uma função \(f\), dizemos que \(g\) é a função inversa de \(f\) se
\[ f(g(x)) = x \]e
\[ g(f(x)) = x \]para todo x em um determinado conjunto. Há mais do que isso, mas deixaremos no nível intuitivo (a rigor, uma função precisa ser injetiva e sobrejetiva para ser invertível, e alguns outros aspectos técnicos que estamos considerando, como restringir o Domínio e alcance , etc.)
Normalmente, chamamos \(f^{-1}\) ao inverso de \(f\), então a fórmula que define o inverso é normalmente escrita como:
\[ f(f^{-1}(x)) = x \]Quais são as etapas para encontrar a função inversa
- Passo 1: Comece com a equação que define a função, ou seja, você começa com y = f(x)
- Passo 2: Você então usa a manipulação algébrica para resolver x. Dependendo de quão complexo é f(x), você pode achar mais fácil ou mais difícil resolver x.
- Etapa 3: Em algumas circunstâncias você simplesmente não será capaz de resolver x, para funções não lineares complexas f(x)
- Passo 4: Se você for capaz de resolver x, então deverá ser capaz de escrever x = g(y)
- Passo 5: Você precisa avaliar se a solução encontrada é única. Isto é, poderia resolver x exclusivamente. Em outras palavras, você encontrou apenas uma solução ao resolver x? Se sim, então você tem uma função inversa, caso contrário, não há inversa
- Passo 6: Se você encontrou o inverso resolvendo x = g(y), basta alterar o nome da variável e escrever f -1 (x) = g(x), o que enfatiza que g(x) É o inverso real
Se você usasse cálculo e derivadas (mas observe que você NÃO precisa Derivativos para calcular o inverso), você pode encontrar a derivada da função e garantir que a derivada seja sempre positiva ou negativa, para garantir que a função seja injetiva e, portanto, invertível.
Mas normalmente, a metodologia de Resolvendo para x é muito mais palatável para estudantes de álgebra básica.
A regra para encontrar funções inversas
Na verdade, não existem outras regras para calcular a função inversa além de começar com y = f(x) e então resolver para x. Uma regra como essa parece bastante ampla, porque é. Mais do que uma regra, é uma metodologia genérica para iniciar o processo.
Em última análise, o cálculo do inverso dependerá do seu sucesso na resolução de uma equação e de garantir que a solução seja única. Ajuda avaliar o gráfico da função de antemão, para não procurar uma inversa quando claramente não há nenhuma.
O que procurar em um gráfico? Uma função precisa ser monótona (crescente ou decrescente) em um determinado subdomínio para ser invertível. Dito isto, poderíamos convenientemente restringir o domínio de uma função a um subdomínio menor para determinar a inversa num conjunto menor, o que é sempre uma possibilidade.

Como sabemos com certeza que a função tem uma inversa?
Formalmente, a única maneira de garantir que uma função tenha uma inversa é garantir que a função seja injetiva (1 para 1). Isto é avaliado calculando sua derivada (se existir) e certificando-se de que ela é positiva e negativa em todos os lugares, ou garantindo manualmente que quando começamos com y = f(x) e resolvemos para x, sempre obteremos um único solução.
Isso também pode ser visto graficamente, usando o teste da linha horizontal: você desenha uma linha horizontal arbitrária, e a função f(x) passa no teste da linha horizontal se qualquer linha horizontal desenhada cruzar o gráfico da função no máximo uma vez.

Exemplo: encontrando a função inversa
Encontre o inverso da seguinte função: \(f(x) = \displaystyle \frac{1}{3} x + \frac{5}{4}\)
Solução:
Temos a seguinte função:
\[f(x) = \frac{1}{3} x + \frac{5}{4}\]Então, para encontrar a inversa da função dada, precisamos resolver \(x\) e determinar se existe uma solução ou não. A equação inicial é:
\[y = \displaystyle \frac{1}{3}x+\frac{5}{4}\]Passo 0: Neste caso, primeiro precisamos simplificar a equação linear dada e, para isso, realizamos as seguintes etapas de simplificação:
Resolvendo a equação linear
Colocando \(x\) no lado esquerdo e \(y\) e a constante no lado direito obtemos
\[\displaystyle -\frac{1}{3}x = -y -\left(-\frac{5}{4}\right)\]Agora, resolvendo para \(x\), dividindo ambos os lados da equação por \(-\frac{1}{3}\), obtém-se o seguinte
\[\displaystyle x=-\frac{1}{-\frac{1}{3}}y+\frac{\frac{5}{4}}{-\frac{1}{3}}\]e simplificando, finalmente obtemos o seguinte
\[\displaystyle x=3y-\frac{15}{4}\]Portanto, a resolução de \(y\) para determinada equação linear leva a \(x=3y-\frac{15}{4}\).
Portanto, e como ao resolver \(x\) encontramos uma solução e é apenas uma solução, encontrámos o inverso.
A função inversa
Com base no trabalho mostrado acima, pode-se concluir que a função inversa é:
\[f^{-1}(x) = 3x-\frac{15}{4}\]A função inversa pode ser representada graficamente da seguinte forma:
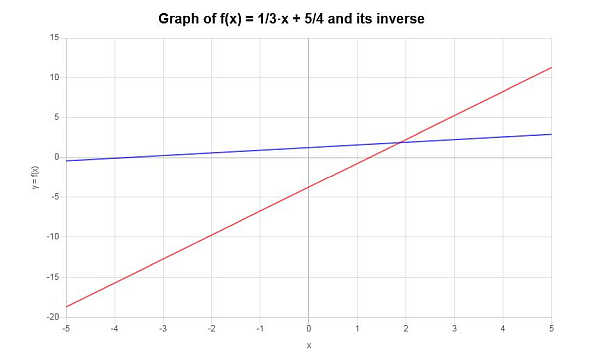
Exemplo: mais exemplos inversos
Calcule a função inversa de: \(y = \frac{x-1}{x+3}\)
Solução:
Para encontrar a inversa da função dada, resolvemos \(x\) e determinamos se existe uma solução ou não. A equação inicial é:
\[y=\frac{x-1}{x+3}\]O seguinte é obtido:
Equação do numerador auxiliar
Precisamos igualar o numerador a zero e encontrar as soluções. Então, aquelas raízes que não tornam o denominador igual a zero serão soluções para a equação racional
Usando a manipulação algébrica da equação polinomial acima, obtém-se o seguinte:
\[x = -\frac{3y+1}{y-1} \]Equação do denominador auxiliar
Encontramos as raízes do denominador: \(x+3=0\)
Portanto, a resolução de \(x\) para determinada equação linear leva a \(x=-3\).
Juntando as soluções da equação racional
Então, verificando se não temos zero no denominador, encontramos a seguinte solução definida para a equação \(\displaystyle y=\frac{x-1}{x+3}\) é
\[x = -\frac{3y+1}{y-1} \]Como quando resolvemos \(x\) encontramos uma e apenas uma solução, concluímos que temos uma função inversa.
Encontrando a função inversa
Com base no trabalho mostrado acima, pode-se concluir que a função inversa é:
\[f^{-1}(x) = -\frac{3x+1}{x-1}\]A função inversa encontrada pode ser representada graficamente como segue:
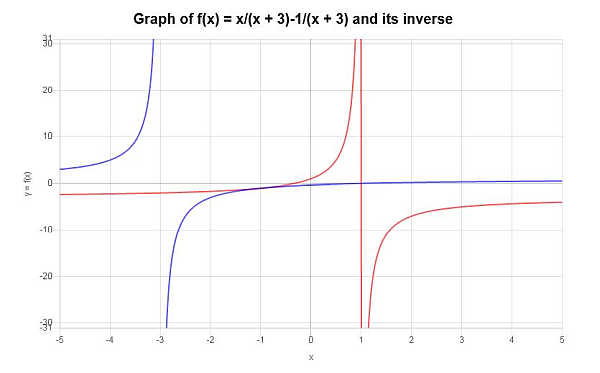
Exemplo: nem todas as funções têm inverso
A seguinte função tem inversa: \( y = \displaystyle \frac{1}{3} x^2 - \frac{2}{5} \) ?
Solução: Observe aquilo
\[ y =\displaystyle \frac{1}{3} x^2 - \frac{2}{5} \] \[ \displaystyle \Rightarrow y + \frac{2}{5} = \frac{1}{3} x^2 \] \[ \displaystyle\Rightarrow x^2 = 3\left(y + \frac{2}{5} \right) \] \[\displaystyle \Rightarrow x = \pm \sqrt{ 3\left(y + \frac{2}{5} \right) }\]o que indica que existem duas soluções e, portanto, não há inverso neste caso.
Mais calculadoras de funções
As funções são um objeto crucial em matemática, especialmente em cálculo e álgebra, onde muitas associações entre variáveis são estabelecidas por meio de funções.
Há muitas coisas que você pode fazer com a função: você pode simplificá-los , você pode diferenciar uma função , você pode operá-los, encontrar o composto com outra função e a lista continua.
Muitas vezes, mesmo que mencione funções explicitamente, você tem funções subjacentes a todo o processo. Então eles estão lá, mesmo que às vezes você não saiba disso. Uma coisa ótima é que mesmo com os muito complicados, você sempre pode gráfico de uma função para ter uma ideia do seu comportamento, para pelo menos ter uma ideia do que a função faz (sobe, desce, etc).




