Como resolver para x

Esta calculadora permitirá que você resolva x para qualquer equação fornecida, mostrando todas as etapas do processo caso uma solução seja encontrada, o que nem sempre é o caso.

Você pode fornecer uma expressão como 'y = x + 1', que é uma função linear simples onde x aparece, ou pode ter algo mais complexo, como 'x^2 + y^2 = 1', onde você terá mais de uma solução.

Depois de fornecer uma expressão válida que envolva x, você pode clicar em "Calcular" para iniciar o processo, e a calculadora tentará resolver x, por resolvendo a equação necessário. Observe a palavra “tentativa”, porque você descobrirá que algumas equações não podem ser resolvidas.

Como você resolve para x?

Não há realmente uma resposta para isso, pois depende muito da estrutura da equação em que x aparece. As equações lineares serão simples de lidar, pois trata-se apenas de mover os termos e dividir a igualdade por um número, se necessário.

Ou para equações quadráticas você terá um tipo de fórmula simples, o bem sabe Fórmula quadrática isso lhe dirá exatamente como resolver x.

Mas para qualquer coisa mais complexa, não é terra de ninguém, e cada equação exigirá a sua própria abordagem, se houver, para ser resolvida.

É por isso que ter um calculadora de equação é muito importante, pois terá uma forma de resolver os tipos de equações mais comuns, além de ter alguns truques para tentar em caso de dificuldade, aumentando suas chances de sucesso.

Etapas para resolver x

• Passo 1: Primeiro, tente identificar o tipo de equação: linear, quadrática, polinomial, racional, radical, logarítmica, exponencial, etc.
• Passo 2: Se você identificou o tipo, então esse tipo específico terá algumas regras específicas a serem resolvidas. Ex: se você descobrir que a equação para x é exponencial, o truque usual para esse tipo de equação é definir uma base comum e igualar os expoentes para resolver a equação
• Etapa 3: Se nenhum tipo específico de equação foi identificado, então você pode seguir algum tipo genérico de roteiro: Tente isolar todos os termos que envolvem x em um lado da equação (dependendo do tipo de equação, isso pode não ser possível)
• Passo 4: Você pode aplicar uma substituição adequada? Você pode simplificar as coisas aplicando uma função ou alguma operação a ambos os lados da igualdade? Esse é basicamente o conselho geral para você começar

Honestamente, isso é tudo que você pode saber como regra geral para resolver equações e resolver x. O resto virá da estrutura específica da equação com a qual você está lidando.

Então não existe fórmula para x?

Em geral não, infelizmente. Para os tipos mais fáceis, você será capaz de encontrar uma fórmula para x, algo como x = g(y), e às vezes esta fórmula irá ajudá-lo a definir um Função inversa , mas às vezes você não encontrará nenhum tipo de fórmula, ou às vezes encontrará mais de uma solução.

Às vezes você terá que restringir as variáveis resolvendo uma desigualdade para encontrar uma solução para x. Isto é, em tais casos, a resolução de x é bem-sucedida apenas em alguma região restrita.

Existe uma diferença entre resolver x e resolver y?

Sim, do ponto de vista de que a variável alvo que você deseja resolver seria diferente, mas não do ponto de vista metodológico, pois as etapas que você executa para resolver x são as mesmas que você executaria para resolver y.

Resolver x ou y ou z envolve o mesmo processo, que é resolver para uma variável específica, o que requer a mesma metodologia. Há casos em que a simetria desempenha um papel, e é até literalmente a mesma. Só para ver de forma concreta, se você tiver a equação \(x^2+y^2=1\), resolver para x levaria exatamente às mesmas etapas que resolver para y. Isso é verdade apenas para este tipo de equações simétricas.

Exemplo: resolva para x

Encontre x em termos de y para: \(\frac{1}{3} y = \frac{x-1}{x+4} - \frac{5}{6}\)

Solução: Neste caso, temos uma equação linear simples, então resolver x é colocar x de um lado:

\[\frac{1}{3} y = \frac{x-1}{x+4} - \frac{5}{6}\] \[ \Rightarrow \frac{1}{3} y = \frac{x-1}{x+4} - \frac{5}{6}\] \[ \Rightarrow \frac{1}{3} y + \frac{5}{6} = \frac{x-1}{x+4}\] \[ \Rightarrow \left( \frac{1}{3} y + \frac{5}{6} \right) (x+4) = x - 1\] \[ \Rightarrow x \left( \frac{1}{3} y + \frac{5}{6} \right) +4 \left( \frac{1}{3} y + \frac{5}{6} \right) = x - 1\] \[ \Rightarrow x \left( \frac{1}{3} y + \frac{5}{6} - 1\right) = - 1 - 4 \left( \frac{1}{3} y + \frac{5}{6} \right)\]

Então, manipulando os termos da equação acima, obtemos a solução:

\[x=-\frac{2\cdot \left(4y+13\right)}{2y-1} \]

Portanto, resolver \(x\) para a equação dada leva à solução \(x=-\frac{2\cdot \left(4y+13\right)}{2y-1}\).

Graficamente

A seguir está a representação gráfica das soluções obtidas com \(y\) expressas em termos de \(\):

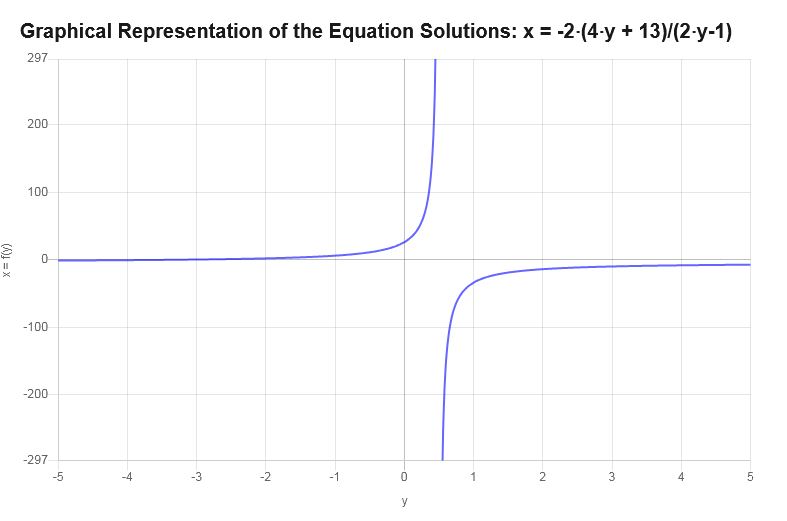
Exemplo: você pode resolver para x?

Você pode resolver para x neste caso: \(y = x^2 - 1\)

Solução: Neste caso, obtemos diretamente que

\[y = x^2 - 1 \Rightarrow x^2 = y + 1\] \[ \Rightarrow x = \pm \sqrt{ y + 1 }\]

Isto implica que somos capazes de encontrar duas soluções, ou "ramos", que são \(x = \sqrt{ y + 1 }\) e \(x = -\sqrt{ y + 1 }\).

Outras calculadoras de equações úteis

Como vimos aqui, resolver x depende muito de Resolvendo equações , o que certamente pode ser um processo desafiador para os tipos mais complexos que não são equações lineares ou quadráticas.

A ideia de resolver para x está intimamente relacionada com encontrando o inverso e também encontrando o gráfico do inverso , pois é exatamente assim que você começa quando está lidando com inversos.

As equações podem ficar mais complicadas quando se trata de equações simultâneas, que requerem algumas técnicas específicas. Um procedimento comum com o qual podemos lidar é Resolvendo sistemas de equações lineares , usando métodos gráficos ou analíticos