Mais sobre o gráfico de funções inversas

Esta calculadora ajuda você a encontrar o gráfico da função inversa que você fornece, desde que a função tenha uma inversa, o que nem sempre é o caso.

Você pode fornecer uma função no formato 'y = 2x - 1' ou simplesmente fornecer uma expressão como 'f(x) = (x-1)/(x-3)' ou apenas '(x-1)/( x-3)' para especificar a função.

Depois de fornecer uma função válida, você pode clicar no botão "Calcular" e serão fornecidos todos os passos do cálculo da função inversa , e se o inverso existir, será mostrado um gráfico com a função e o inverso.

Observe que para que a função dada tenha uma função inversa, a função precisa ser bijetiva, o que significa que todo valor no contradomínio da função possui no máximo uma pré-imagem no domínio da função, e exatamente uma pré-imagem restringimos o alcance efetivo.

Como saber se uma função é invertível

Antes de obter o gráfico da inversa de uma determinada função, você precisa saber se a função tem alguma inversa. O principal critério para se ter um inverso é ser um para um, o que significa que um valor no intervalo não pode ter dois valores associados (pré-imagens).

Possivelmente os alunos preferem não usar termos técnicos como 'imagens' e 'pré-imagens' e, embora esses sejam conceitos centrais na teoria das funções, neste caso podemos usar um teste gráfico simples para avaliar se uma função é ou não injetora. um e, portanto, se você puder encontrar e representar graficamente seu inverso.

Teste de linha horizontal

O teste da linha horizontal indica que, para que uma função seja injetora, qualquer linha horizontal que você construir cruzará o gráfico da função no máximo uma vez. Se você conseguir encontrar uma linha horizontal que cruze o gráfico de uma determinada função mais de uma vez, então a função NÃO É bijetora.

Por exemplo, a função mostrada abaixo é injetora, porque não importa qual linha horizontal lançarmos sobre ela, ela cruzará o gráfico da função exatamente uma vez:

Mas então, o próximo exemplo mostra uma função que não é injetora, porque vemos uma linha horizontal que cruza a linha da função 2 vezes (mais de uma vez):

Etapas para encontrar o gráfico inverso

• Passo 1: Existem dois métodos comuns: um é o método gráfico e o outro é o método analítico
• Passo 2: Para o método gráfico, você precisa primeiro aplicar o teste da linha horizontal e certificar-se de que ele passa, então é um para um e o inverso existe
• Etapa 3: Então, você desenha a linha y = x no gráfico (uma linha reta que tem um ângulo de 45 ^o graus em relação ao eixo x
• Passo 4: Depois disso, basta usar a reta y = x como um 'espelho' e refletir os pontos do gráfico original em relação ao 'espelho'. O gráfico obtido com este processo de espelhamento é o gráfico do inverso
• Passo 5: Para o método analítico, você precisa primeiro calcular algebricamente encontre o inverso : Você começa com y = f(x) e depois resolve para y.
• Passo 6: Se houver apenas uma solução, então o inverso existe e você o escreve x = g(y). Ajustando os nomes das variáveis, você define formalmente a função inversa \(f^{-1}\) em termos de g
• Etapa 7: Finalmente, você representa graficamente o inverso que encontrou \(f^{-1}\) como faria gráfico de uma função normalmente

Quando você precisa encontrar o gráfico inverso, tanto o método gráfico quanto o analítico servem, só o método analítico tem uma vantagem, que é que você calcula a função inversa ao longo do processo, então você acaba tendo uma expressão matemática disso, não apenas seu gráfico.

Por que você representaria graficamente o inverso

Há tantos motivos pelos quais você faria isso. Primeiro, a função inversa em si é um ator muito importante na teoria das funções, pois uma função mostra como passar de x para ay, então é natural querer saber qual é o mecanismo para passar de y para x, e isso é exatamente o que a função inversa fornece.

Portanto, pode-se pensar em uma função como um mapa unidirecional de um ponto "X" a um ponto "Y", e calcular a função inversa é como definir explicitamente um mapa para ir de "Y" a "X".

E então o gráfico da inversa lhe dará muitas informações sobre essa função inversa: ela desce para cima, como ela se comporta.

Como esta calculadora de função gráfica inversa me ajuda?

Primeiro, esta calculadora analisará a função para ver se ela é invertível usando o método analítico e, se for possível encontrar tal inversa, ela fará um gráfico para você.

Encontrar o inverso envolve resolvendo uma equação , o que não é uma tarefa fácil, a menos que você esteja lidando com Equações Lineares ou equações polinomiais , mas fora isso, o processo pode ser muito complexo ou até impossível.

Outras calculadoras podem fazer um processo semelhante, mas uma das vantagens de esta calculadora é que fornece todas as etapas do processo, com explicação detalhada, sempre que possível.

Exemplo: encontrando o gráfico do inverso

Faça um gráfico do inverso de: \( y = \frac{2}{3} x - \frac{5}{6}\)

Solução:

Recebemos a seguinte função:

\[ y = \frac{2}{3} x - \frac{5}{6}\]

Então, para encontrar a inversa da função dada, precisamos resolver \(x\) e determinar se existe uma solução ou não. A equação inicial é

\[y=\frac{2}{3}x-\frac{5}{6}\]

Passo 0: Neste caso, primeiro precisamos simplificar a equação linear dada e, para isso, realizamos as seguintes etapas de simplificação:

Resolvendo a equação linear

Colocando \(x\) no lado esquerdo e \(y\) e a constante no lado direito obtemos

\[\displaystyle -\frac{2}{3}x = -y -\frac{5}{6}\]

Agora, resolvendo para \(x\), dividindo ambos os lados da equação por \(-\frac{2}{3}\), obtém-se o seguinte

\[\displaystyle x=-\frac{1}{-\frac{2}{3}}y-\frac{\frac{5}{6}}{-\frac{2}{3}}\]

e simplificando, finalmente obtemos o seguinte

\[\displaystyle x=\frac{3}{2}y+\frac{5}{4}\]

Portanto, a resolução de \(y\) para determinada equação linear leva a \(x = \frac{3}{2}y+\frac{5}{4}\).

Portanto, e como ao resolver \(x\) encontramos uma solução e é apenas uma solução, encontrámos o inverso.

A função inversa encontrada

Com base no trabalho mostrado acima, pode-se concluir que a função inversa é:

\[f^{-1}(x) = \frac{3}{2}x+\frac{5}{4}\]

A função inversa pode ser mostrada graficamente da seguinte forma:

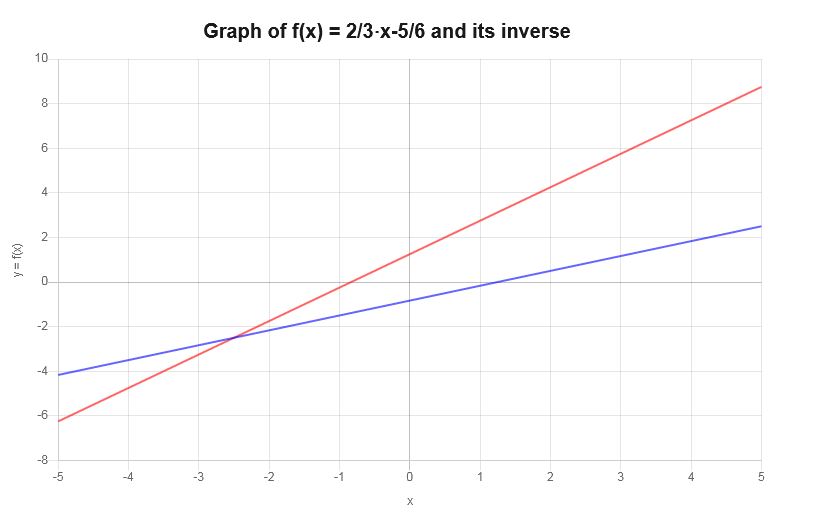
Exemplo: mais gráficos inversos

Você consegue encontrar o gráfico inverso de: \(y = x^2\)

Solução: Não, não podemos encontrar o gráfico inverso de \(y = x^2\), pois esta função não passa no teste da linha horizontal. Outra maneira de ver isso é que ao resolver \(x\) obtemos \(x = \pm \sqrt y\), e como encontramos duas soluções, então não há inverso e, consequentemente, não há gráfico inverso.

Mais calculadoras de funções

Funções e qualquer tipo de operação de função são verdadeiramente o centro da Álgebra e do Cálculo. Um bem calculadora de funções facilitará sua vida em termos de reduzir uma função à sua expressão mais simples.

Então você terá um bom ferramenta gráfica de funções para dar uma rápida olhada nas propriedades gráficas de uma função. Ver o gráfico de uma função pode dizer muito sobre seu comportamento, mesmo antes de olhar para sua expressão algébrica.

Então você tem operações mais avançadas, como encontrar a derivada, para a qual este Calculadora de Diferenciação será útil, pois mostra todas as etapas do processo. Como esperado, a derivada da função inversa tem uma associação interessante com a derivada da função original.