Mais sobre equações lineares

Esta calculadora irá ajudá-lo a representar graficamente uma equação linear que você fornecer. Então, o primeiro passo é fornecer uma equação linear válida, algo como 2x + 3y = 4, ou você também pode fornecer algo que não vem diretamente simplificado, como 2/3 x + y = 4/3 x - 1/ 2 y + 2. Qualquer expressão linear válida funcionará. .

Depois de fornecer uma equação linear válida, a parte fácil entra em ação, pois tudo o que você precisa fazer é clicar em "Calcular" e as etapas do processo de representação gráfica da função linear serão mostradas a você.

As equações lineares desempenharão um papel importante em muitas operações, inclusive para resolver um sistema de equações lineares .

Fórmula de equação linear

Existem diferentes formas nas quais você pode escrever uma fórmula de equação linear. Os mais comuns são os formulário padrão , que é mostrado abaixo

\[a x + by = c \]

Também, existe o forma de intercepção de encostas , que é mostrado abaixo

\[y = mx + n\]

Essas duas formas podem ser convertidas de uma para outra, exceto por algumas exceções, a saber, a linha vertical expressa por x = a. Esta linha é vertical e cruza o eixo x em (a, 0). Temos que x = a é a forma padrão da linha, mas esta linha não tem interceptação de inclinação (pelo menos onde y é a variável dependente)

Quais são os passos para representar graficamente uma equação linear?

• Passo 1: Identifique claramente a equação disponível
• Passo 2: Veja o coeficiente que multiplica y, se for zero, então você tem uma linha vertical
• Etapa 3: Se o coeficiente que multiplica y for diferente de zero, você resolve y para obter o forma de intercepção de encostas
• Etapa 4: usando a forma de interceptação da inclinação, calcule a função em x = 0 e x = 1 e, a seguir, você terá dois pontos por onde a reta passa
• Etapa 5: desenhe uma linha usando os dois pontos encontrados como guia

Uma das maneiras mais claras de traçar uma linha é ter dois pontos por onde a linha passa, pois muitas vezes usar a inclinação para se guiar pode ser enganoso.

Solução da equação linear em uma variável

Os alunos estão familiarizados com sistemas de equações lineares e entendem mais ou menos o que precisa ser feito. Mas então eles se perguntam sobre a solução de uma equação linear em uma variável. Digamos que você tenha a equação linear na forma de interceptação de inclinação:

\[y = a + bx \]

Então, como você resolve isso? Bem, já está resolvido: para cada valor dado de x, a solução de y é y = a + bx. Portanto, desde que \(b \ne 0\), você tenha infinitas soluções para uma equação linear.

A situação muda quando você tem duas equações lineares, caso em que você precisa resolva as duas equações simultaneamente .

As equações lineares são tão importantes?

Pode apostar! Talvez entre os mais importantes em toda a matemática. Isso se deve à simplicidade e ainda à vasta gama de aplicações.

Exemplo: calculadora de equações lineares

Obtenha o gráfico da seguinte equação linear: \(\frac{1}{3} x + \frac{7}{4} y - \frac{5}{6} = 0\)

Solução:

Obtenha a equação da linha na forma de interceptação de inclinação

A seguinte equação nos foi dada.:

\[\displaystyle \frac{1}{3}x+\frac{7}{4}y-\frac{5}{6}=0\]

Simplificando as constantes:

\[\displaystyle \frac{1}{3}x+\frac{7}{4}y-\frac{5}{6}=0\]

Agora, colocando \(y\) no lado esquerdo e \(x\) e a constante no lado direito, obtemos

\[\displaystyle \frac{7}{4}y = -\frac{1}{3}x + \frac{5}{6}\]

Agora, resolvendo para \(y\), dividindo ambos os lados da equação por \(\frac{7}{4}\), obtém-se o seguinte

\[\displaystyle y=-\frac{\frac{1}{3}}{\frac{7}{4}}x+\frac{\frac{5}{6}}{\frac{7}{4}}\]

e simplificando, finalmente obtemos o seguinte

\[\displaystyle y=-\frac{4}{21}x+\frac{10}{21}\]

Conclusão : Inferimos que a equação da linha na forma de interceptação de inclinação é baseada nos dados disponíveis: \(\displaystyle y=-\frac{4}{21}x+\frac{10}{21}\), com uma inclinação de \(\displaystyle b = -\frac{4}{21}\) e interceptação y de \(\displaystyle n = \frac{10}{21}\).

Considerando esses dados, o gráfico de linha fornecido mostra

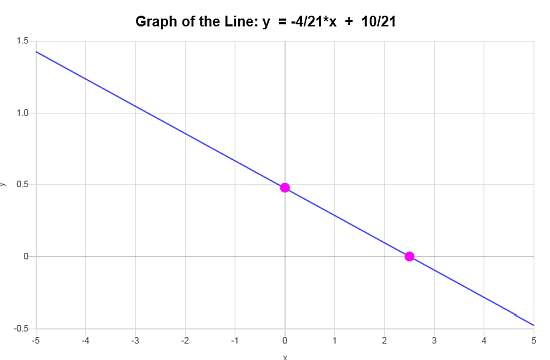
Exemplo: exemplo de calculadora de equação linear

Calcule o seguinte: \(\frac{1}{3}x + \frac{5}{4}y = \frac{1}{6}\)

Solução: Agora temos a seguinte equação:

\[\displaystyle \frac{1}{3}x+\frac{5}{4}y=\frac{1}{6}\]

O primeiro passo é simplificar as constantes:

\[\displaystyle \frac{1}{3}x+\frac{5}{4}y=\frac{1}{6}\]

Colocando \(y\) no lado esquerdo e \(x\) e o termo constante no lado direito, obtemos

\[\displaystyle \frac{5}{4}y = -\frac{1}{3}x +\frac{1}{6}\]

Agora, precisamos resolver para \(y\), e isso é obtido dividindo ambos os lados da equação por \(\frac{5}{4}\), e o seguinte é obtido

\[\displaystyle y=-\frac{\frac{1}{3}}{\frac{5}{4}}x+\frac{\frac{1}{6}}{\frac{5}{4}}\]

e simplificando, finalmente obtemos o seguinte

\[\displaystyle y=-\frac{4}{15}x+\frac{2}{15}\]

Conclusão : A equação da linha na forma de interceptação de inclinação é, de acordo com as informações fornecidas, \(\displaystyle y=-\frac{4}{15}x+\frac{2}{15}\), com uma inclinação de \(\displaystyle b = -\frac{4}{15}\) e interceptação y de \(\displaystyle n = \frac{2}{15}\).

De acordo com esses dados, o gráfico de linha apresentado é

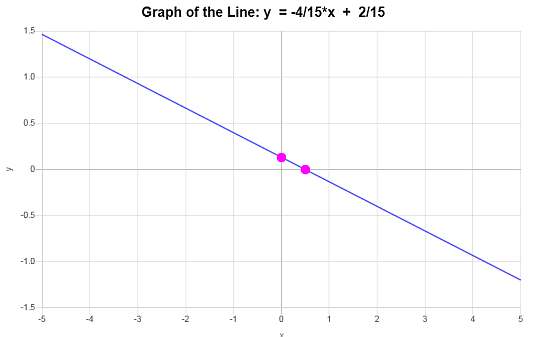
Exemplo: outro exemplo de calculadora de equação linear

Isso representa uma linha: \( y = 5 \). Se sim, quais são suas características?

Solução: Sim. De fato, quando você tem uma expressão como \( y = 5 \), você tem uma equação linear na forma de interceptação de inclinação, com a = 0 e b = 5. Portanto, o que temos é uma linha que é horizontal, que cruza o y -eixo no ponto (0, 5).

Mais calculadoras de álgebra

Linhas , Equações Lineares e funções lineares sempre terá um papel crucial na Álgebra, apresentando também uma ligação clara com algumas propriedades geométricas básicas.

Em termos de aplicações, talvez Resolvendo sistemas de equações lineares está entre as aplicações mais comuns de linhas e equações lineares.