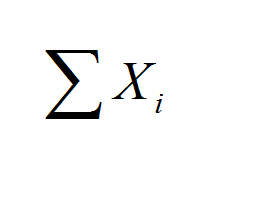Solventes Álgebra

Calculadora pemdas

Instruções: Use esta calculadora para calcular e simplificar qualquer expressão (numérica ou simbólica) que você fornecer, seguindo as regras do PEMDAS, mostrando todas as etapas. Por favor, digite a expressão que deseja calcular na caixa de formulário abaixo.

Sobre esta calculadora pemdas

Esta calculadora permite simplificar parênteses, expressões de multiplicação , dividir expressões e adicionar e subtrair expressões , formando uma expressão composta mais complexa que pode ser resolvida com regras PEMDAS .

Tudo o que você precisa fazer é fornecer uma expressão válida, seja simbólica ou numérica, e todas as etapas da simplificação serão mostradas para você.

Uma vez fornecida uma expressão válida, entra a parte fácil: basta clicar no botão "Calcular" e pronto, todos os passos estarão aí para você.

O processo de simplificação de expressões pode ser sutil, especialmente se você fornecer à calculadora uma expressão complexa.

Calculadora pemdas com expoentes

Esta calculadora conduz PEMDAS para expoentes? Absolutamente! De fato, PEMDAS tem o 'E' para expoentes, então a prioridade dos expoentes é muito alta em um processo de simplificação, apenas superada por parênteses.

Até certo ponto, parênteses e expoentes permitem que você veja algumas expressões 'isoladas' que podem ser tratadas separadamente. Por exemplo, se você tiver \(2^{\frac{1}{2} + \frac{1}{3}}\), a soma da fração no expoente é como 'isolada' e você pode começar a simplificar aí.

Quais são as etapas para usar o pemdas?

Etapa 1: comece com os parênteses e expoentes (nessa ordem), procurando subexpressões que podem ser tratadas primeiro
Passo 2: Uma vez identificadas essas subexpressões, use o PEMDAS para resolvê-las. Ou seja, ainda pode haver parênteses ou expoentes que precisam ser tratados primeiro e têm prioridade
Etapa 3: quando você chegar a um parênteses ou expoente interno mais avançado, poderá ver quais operações simples permanecem, dando prioridade à multiplicação e divisão e, em seguida, realizando adições e subtrações

Em última análise, o PEMDAS pode ser aplicado trivialmente em alguns casos triviais, mas nem sempre é o caso. O PEMDAS tem essa natureza potencialmente recursiva, que pode tornar sua aplicação confusa, especialmente com expressões aninhadas particularmente complexas.

No final, na maioria dos casos você não terá que pensar muito, pois a maioria dos casos usuais são bem simples, mas é bom ter a consciência de que o PEMDAS pode ser tão complexo quanto a complexidade da expressão fornecida você quer simplificar.

Por que o pemdas é importante?

O PEMDAS é importante porque é a única forma que temos de garantir que haja uma única forma correta de simplificação. Agora, pode haver caminhos diferentes que levem a essa simplificação correta, mas serão todos iguais.

simplificando expressões precisa ser um esforço exato, e é disso que se trata o PEMDAS.

Exemplo: exemplo pemdas

Calcular: \(\frac{1}{3} \frac{2}{3} + \frac{5}{4} - \frac{1}{6}\)

Solução: Temos a seguinte expressão: \(\displaystyle \frac{1}{3}\cdot\frac{2}{3}+\frac{5}{4}-\frac{1}{6}\).

Obtém-se o seguinte cálculo:

\( \displaystyle \frac{1}{3}\cdot \frac{2}{3}+\frac{5}{4}-\frac{1}{6}\)

We can multiply the terms in the top and bottom, and we get \(\displaystyle\frac{ 1}{ 3} \times \frac{ 2}{ 3}= \frac{ 2}{ 3 \times 3} \)

\( = \,\,\)

\(\displaystyle \frac{2}{3\cdot 3}+\frac{5}{4}-\frac{1}{6}\)

By multiplying the terms in the denominator, we get: \( 3 \times 3 = 9\)

\( = \,\,\)

\(\displaystyle \frac{2}{9}+\frac{5}{4}-\frac{1}{6}\)

Amplifying in order to get the common denominator 36

\( = \,\,\)

\(\displaystyle \frac{2}{9}\cdot\frac{4}{4}+\frac{5}{4}\cdot\frac{9}{9}-\frac{1}{6}\cdot\frac{6}{6}\)

We use the common denominator: 36

\( = \,\,\)

\(\displaystyle \frac{2\cdot 4+5\cdot 9-1\cdot 6}{36}\)

Expanding each term: \(2 \times 4+5 \times 9-6 = 8+45-6\)

\( = \,\,\)

\(\displaystyle \frac{8+45-6}{36}\)

Adding up each term in the numerator

\( = \,\,\)

\(\displaystyle \frac{47}{36}\)

que conclui o processo de simplificação.

Exemplo: mais exemplos de pemdas

Simplifique o seguinte: \( \left(\frac{2}{3} + \frac{5}{4}\right)^2 - \frac{5}{6}\)

Solução: Temos a seguinte expressão: \(\displaystyle \left(\frac{2}{3}+\frac{5}{4}\right)^2-\frac{5}{6}\).

Obtém-se o seguinte cálculo:

\( \displaystyle \left(\frac{2}{3}+\frac{5}{4}\right)^2-\frac{5}{6}\)

Amplifying in order to get the common denominator 12

\( = \,\,\)

\(\displaystyle \left(\frac{2}{3}\cdot \frac{4}{4}+\frac{5}{4}\cdot \frac{3}{3}\right)\left(\frac{2}{3}\cdot \frac{4}{4}+\frac{5}{4}\cdot \frac{3}{3}\right)-\frac{5}{6}\)

We use the common denominator: 12

\( = \,\,\)

\(\displaystyle \left(\frac{2\cdot 4+5\cdot 3}{12}\right) \times \left(\frac{2\cdot 4+5\cdot 3}{12}\right)-\frac{5}{6}\)

Expanding each term: \(2 \times 4+5 \times 3 = 8+15\)

\( = \,\,\)

\(\displaystyle \left(\frac{8+15}{12}\right) \times \left(\frac{8+15}{12}\right)-\frac{5}{6}\)

Operating the terms in the numerator

\( = \,\,\)

\(\displaystyle \frac{23}{12}\cdot\frac{23}{12}-\frac{5}{6}\)

We can multiply the terms in the top and bottom as in \(\displaystyle\frac{ 23}{ 12} \times \frac{ 23}{ 12}= \frac{ 23 \times 23}{ 12 \times 12} \)

\( = \,\,\)

\(\displaystyle \frac{23\cdot 23}{12\cdot 12}-\frac{5}{6}\)

Multiplication of terms in the numerator and denominator, we get: \( 23 \times 23 = 529 \) and \( 12 \times 12 = 144\)

\( = \,\,\)

\(\displaystyle \frac{529}{144}-\frac{5}{6}\)

Amplifying in order to get the common denominator 144

\( = \,\,\)

\(\displaystyle \frac{529}{144}-\frac{5}{6}\cdot\frac{24}{24}\)

We use the common denominator: 144

\( = \,\,\)

\(\displaystyle \frac{529-5\cdot 24}{144}\)

Expanding each term in the numerator: \(529-5 \times 24 = 529-120\)

\( = \,\,\)

\(\displaystyle \frac{529-120}{144}\)

Operating the terms in the numerator

\( = \,\,\)

\(\displaystyle \frac{409}{144}\)

que conclui o processo de simplificação.

Mais calculadoras de álgebra

Um dos pilares da álgebra é a manipulação de expressões algébricas , de números a frações, a expressões compostas complicadas.

Toda a adivinhação é removida quando se tem um conjunto adequado de regras que estabelecem o correto ordem de operações em que a expressão deve ser simplificada.