Risolutori Calcolo

Calcolatrice di differenziazione implicita

Istruzioni: Utilizza questo calcolatore di differenziazione implicita per calcolare la derivata \(\frac{dy}{dx}\), quando \(x\) e \(y\) sono collegati tramite un'equazione. Fornisci un'equazione che coinvolga xey nella casella del modulo sottostante.

Differenziazione implicita

Questa calcolatrice ti aiuterà a condurre la differenziazione implicita per un'equazione che coinvolge le variabili x e y. Devi fornire un'equazione valida come x^2 + y^2 = 1, o xy - x^2 y^2 = 0, ecc.

Una volta fornita un'equazione valida che coinvolge due variabili (\(x\) e \(y\)), tutto ciò che devi fare è cliccare sul pulsante "Calcola", e verranno mostrati tutti i passaggi della corrispondente derivazione implicita.

Questo è un calcolatrice dy/dx con passaggi nel senso che ti mostrerà tutti i passaggi rilevanti del calcolo della derivata di una variabile rispetto a un'altra, purché queste due variabili siano correlate in un'unica equazione. Questa relazione è ciò che ti permette di trovare il corrispondente derivata implicita .

Avere un'equazione che mette in relazione le due variabili \(x\) e \(y\) ci dice che dovremmo essere in grado di esprimere \(y\) in funzione di \(x\) e scrivere \(y = y(x)\). Spesso non possiamo esprimere esplicitamente \(y\) come una funzione di \(x\), supponiamo che esista tale funzione, nel qual caso ha senso differenziare \(y\) rispetto a \(x\).

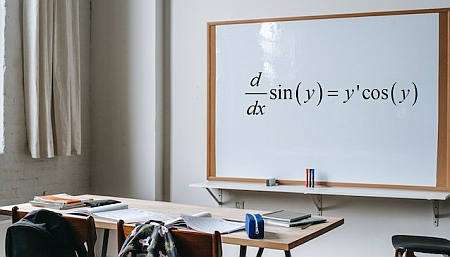
Calcolatrice Di Differenziazione Implicita

Cos'è la differenziazione implicita?

La differenziazione implicita è a calcolo della differenziazione tecnica basata sul presupposto che sia possibile affermare da una data equazione che coinvolge \(x\) e \(y\) che \(y\) è una funzione di \(x\) anche se spesso non possiamo scrivere esplicitamente tale funzione.

Una volta fatta questa ipotesi, assumiamo di poter calcolare \(\frac{dy}{dx}\) e di poter utilizzare tutto ciò che sappiamo Regole derivate ( Regola Del Prodotto , Regola Del Quoziente E Regola Di Derivazione ) per differenziare entrambi i lati dell'equazione e risolvere \(\frac{dy}{dx}\).

Qual è il metodo di differenziazione implicita?

Il metodo di differenziazione implicita è un metodo che consente di calcolare una derivata di espressioni che non sono inserite direttamente nel formato \(f(x)\). Questo è, quando viene data una funzione di una variabile \(x\), ad esempio, semplicemente andiamo avanti e differenziamo quella funzione.

Ma quando due variabili \(x\) e \(y\) sono correlate tramite un'equazione, come ad esempio \(x^2+y^2 = 1\), puoi anche differenziare y rispetto a x, con il metodo tradizionale, dovrai RISOLVERE y in termini di x, e POI puoi differenziare.

Usando la differenziazione implicita, puoi differenziare direttamente, partendo solo dal presupposto che \(y = y(x\) e facendo uso di Regola Di Derivazione .

Passaggi per l'utilizzo della differenziazione implicita

Passo 1: Identificare l'equazione che coinvolge due variabili x e y. Semplifica eventuali termini ridondanti
Passo 2: Supponiamo che y sia una funzione di x, y = y(x), quindi ha senso calcolare la derivata di y rispetto a x
Passaggio 3: Calcola la derivata di entrambi i lati dell'equazione utilizzando tutti i Regole derivate hai bisogno. Questo porterà ad un'uguaglianza in cui x, y e y' sono presenti potenzialmente
Passaggio 4: Risolvi ciò che hai ottenuto nel passaggio 3 per te. Nota che y' sarà solitamente scritto come una funzione di x e y, il che va bene, dato che y dipende anche da x

Questa è una metodologia molto generale e avrà sottigliezze da caso a caso, ma questo è il progetto che dovrebbe funzionare nella maggior parte dei casi, con l'aggiunta di potenziali difficoltà di manipolazione algebrica.

Perché utilizzare un calcolatore di differenziazione implicita

La differenziazione implicita potrebbe a volte creare confusione, se non si è molto chiari su cosa si differenzia e rispetto a quale variabile. Un calcolatore ti aiuterà a confrontare il tuo risultato e una cosa speciale del nostro calcolatore è che vengono mostrati tutti i passaggi del processo.

Questo è un aiuto fondamentale per te, perché ti mostrerà esattamente quale regola derivata e dove l'hai applicata.

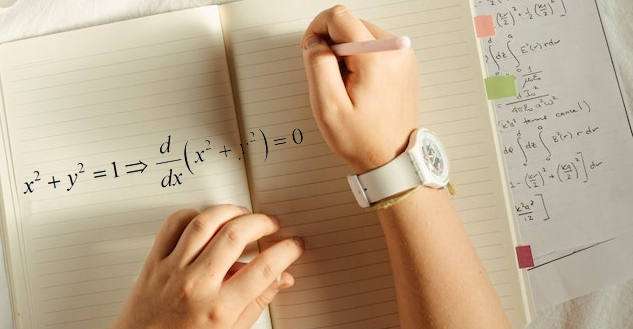
Calcolo Della Differenziazione Implicita

Qual è il punto della differenziazione implicita?

Questa è una domanda giusta. Se hai un'equazione che coinvolge x e y, perché non risolvere y in termini di x e usare il normale calcolo della derivata per ottenere la derivata di y rispetto a x. Posso darti almeno due buoni motivi:

Motivo 1: Potrebbe essere il caso in cui NON PUOI risolvere y in termini di x in modo esplicito. Potrebbe esserci una funzione, ma non puoi semplicemente trovarla. Pensa a y + tan(y) = x^2
Motivo 2: Anche se ti capita risolvere y in termini di x , potrebbe essere un'espressione davvero complicata e il calcolo della derivata potrebbe essere molto contorto e difficile. Di solito, la differenziazione implicita è algebricamente semplice, in termini relativi

La derivata implicita dipende da y?

Non sempre, ma spesso. Ora, questo dice solo che \(\frac{dy}{dx}\) può dipendere da xey, ma poiché y dipende da x, sta solo dicendo che come previsto \(\frac{dy}{dx}\) dipende da x.

Diversi esempi di differenziazione implicita saranno presentati nella sezione seguente.

Seconda derivata implicita

Una domanda è: è possibile calcolare la derivata seconda utilizzando la differenziazione implicita? La risposta è si. Fai semplicemente lo stesso della derivata prima usando la differenziazione implicita, presumi semplicemente che \(y\) sia una funzione di \(x\), quindi scrivi \(y = y(x)\) e puoi differenziare quanto desideri.

Ad esempio, supponiamo che tu voglia trovare \(\frac{d^2y}{dx^2}\) data l'equazione \(x^2+y^2=1\). Differenziando entrambi i lati rispetto a \(x\):

\[ \frac{d}{dx}\left(x^2+y^2\right)=\frac{d}{dx}\left(1\right)\] \[ \Rightarrow 2x+2yy' = 0\]

Ora differenziamo nuovamente rispetto a x:

\[ \frac{d}{dx}\left(2x+2yy'\right)=\frac{d}{dx}\left(0\right)\] \[ \Rightarrow 2+2(y')^2+2yy'' = 0\]

e ora risolviamo \(y''\):

\[ \Rightarrow y'' = -\frac{(2+2(y')^2)}{2y}\] \[ \Rightarrow y'' = -\frac{(1+(y')^2)}{y}\]

Esempio: esempio di differenziazione implicita

Trova \(\frac{dy}{dx}\) per l'equazione: \(x^2 - y^2 = 2y\)

Soluzione: Questo è un esempio di differenziazione implicita. È stata fornita la seguente equazione: \(\displaystyle x^2-y^2=2y\), per la quale dobbiamo effettuare una differenziazione implicita, dove assumiamo che \(y\) sia una funzione di \(x\) .

L'equazione non ha bisogno di ulteriore semplificazione, quindi possiamo procedere con la differenziazione implicita:

Dobbiamo differenziare entrambi i lati dell'equazione rispetto a \(x\), e su entrambi i lati assumiamo che \(y = y(x)\).

Lato sinistro : Differenziare il lato sinistro rispetto a \(x\)

\( \displaystyle \frac{d}{dx}\left(x^2-y^2\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^2-y^2 \right) = \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(y^2\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(y^2\right)\)

Using the Chain Rule: \(\frac{d}{dx}\left( y^2 \right) = 2y\cdot \frac{d}{dx}\left(y\right)\) and using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x-2y\cdot \frac{d}{dx}\left(y\right)\)

We assume that \(y\) is a function of \(x\): \(\frac{d}{dx}\left( y \right) = \frac{dy}{dx}\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x-2y\cdot \frac{dy}{dx}\)

Lato destro : Differenziare il lato destro rispetto a \(x\)

\( \displaystyle \frac{d}{dx}\left(2y\right)\)

Since it is a constant times \(y\), we directly get: \(\frac{d}{dx}\left( 2y \right) = 2 \cdot \frac{d}{dx}\left(y\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle 2 \cdot \frac{d}{dx}\left(y\right)\)

We assume that \(y\) is a function of \(x\): \(\frac{d}{dx}\left( y \right) = \frac{dy}{dx}\)

\( \displaystyle = \,\,\)

\(\displaystyle 2 \cdot \frac{dy}{dx}\)

Pertanto, dopo aver differenziato entrambi i lati rispetto a \(x\) si ottiene quanto segue:

\[\displaystyle 2x-2y\frac{dy}{dx} = 2\frac{dy}{dx}\]

Mettendo da una parte tutti i termini:

\[-2\,y\frac{d}{dx}y+2\,x-2\,\frac{d}{dx}y = 0\]

Raggruppare tutto ciò che contiene \(\displaystyle \frac{dy}{dx}\):

\[-2\,{\left(y+1\right)}\frac{d}{dx}y+2\,x = 0\]

Infine, risolvendo \(\displaystyle \frac{dy}{dx}\), si ottiene:

\[\displaystyle \frac{dy}{dx} = \frac{x}{y+1}\]

Esempio: calcoli di differenziazione più implicita

Qual è la pendenza della linea tangente ad una circonferenza unitaria nel punto \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\)

Soluzione: Si noti che l'equazione della circonferenza unitaria è \(\displaystyle x^2 + y^2 = 1\), che definisce implicitamente \(y\) come funzione di \(x\). Per trovare la linea tangente, dobbiamo calcolare \(\frac{dy}{dx}\) nel punto specificato. Usando la differenziazione implicita, differenziamo entrambi i lati dell'equazione che definisce il cerchio unitario: \[\displaystyle x^2 + y^2 = 1\] \[\Rightarrow \displaystyle \frac{d}{dx}\left(x^2 + y^2\right) = \frac{d}{dx}\left(1\right)\] \[\Rightarrow \displaystyle 2x+2yy' = 0 \] \[\Rightarrow \displaystyle 2yy' = -2x \] \[\Rightarrow \displaystyle y' = -\frac{x}{y} \]

Il punto di interesse è \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\), quindi .

\[\displaystyle y' \left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right) = -\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = -1\]

Ciò implica che la pendenza della linea tangente nel punto \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\) è \(m = -1\), il che implica che l'equazione della linea tangente in quel punto è

\[\displaystyle y - \frac{\sqrt{2}}{2} = -\left(x-\frac{\sqrt{2}}{2}\right)\] \[\Rightarrow \displaystyle y = \frac{\sqrt{2}}{2} - x + \frac{\sqrt{2}}{2}\] \[\Rightarrow \displaystyle y = \sqrt{2} - x \]

Esempio di differenziazione implicita

Considera l'equazione: \( \displaystyle \frac{2}{3} x + y^2 = \frac{2}{5} \). Calcola \(\frac{dy}{dx}\)

Soluzione: In questo caso abbiamo la seguente equazione: \(\displaystyle \frac{2}{3} x + y^2 = \frac{2}{5}\), quindi dobbiamo fare una differenziazione implicita, partendo dal presupposto che \(y\) dipende da\(x\) .

Non è richiesta un'ulteriore semplificazione dell'equazione, permettendoci quindi di procedere con la differenziazione implicita:

Ora dobbiamo calcolare la derivata di entrambi i membri rispetto alla variabile \(x\), assumendo che \(y = y(x)\).

Lato sinistro : Differenziando il lato sinistro rispetto alla variabile \(x\)

\( \displaystyle \frac{d}{dx}\left(\frac{2}{3}x+y^2\right)\)

Usando la linearità, conosciamo \(\frac{d}{dx}\left( \frac{2}{3}x+y^2 \right) = \frac{d}{dx}\left(\frac{2}{3}x\right)+\frac{d}{dx}\left(y^2\right)\), quindi collegalo:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(\frac{2}{3}x\right)+\frac{d}{dx}\left(y^2\right)\)

Dobbiamo usare la Regola della Catena: \(\frac{d}{dx}\left( y^2 \right) = 2y\cdot \frac{d}{dx}\left(y\right)\) e direttamente otteniamo: \(\frac{d}{dx}\left( \frac{2}{3}x \right) = \frac{2}{3}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2}{3}+2y\cdot \frac{d}{dx}\left(y\right)\)

Supponendo che \(y\) sia una funzione di \(x\): \(\frac{d}{dx}\left( y \right) = \frac{dy}{dx}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2}{3}+2y\cdot \frac{dy}{dx}\)

Lato destro : Ora differenziamo il lato destro rispetto a \(x\)

\( \displaystyle \frac{d}{dx}\left(\frac{2}{5}\right)\)

L'espressione è una costante, quindi la sua derivata è 0

\( \displaystyle = \,\,\)

\(\displaystyle 0\)

Quindi, il risultato che si ottiene dopo aver differenziato entrambi i lati rispetto a \(x\) è:

\[\displaystyle \frac{2}{3}+2y\frac{dy}{dx} = 0\]

Pertanto, ora possiamo risolvere \(\displaystyle \frac{dy}{dx}\) per ottenere:

\[\displaystyle \frac{dy}{dx} = -\frac{1}{3\,y}\]

Risolutori di calcolo più utili

Una delle applicazioni più interessanti del regole delle derivate è il concetto di differenziazione implicita. Ha applicazioni in fisica, economia e ingegneria ed è estremamente pratico per descrivere il tasso di variazione lungo le curve.

Un diverso tipo di derivati sono derivate parziali in cui, contrariamente al caso di differenziazione implicita in cui assumiamo che y = y(x), in tal caso y è considerata una costante quando x cambia.