Calcolatore di periodo e frequenza

Quando si tratta di funzioni periodiche, ci sono alcuni parametri cruciali che devono essere calcolati, e questi sono il periodo (\(P\)) e la frequenza (\(f\)).

Il periodo \(P\) di una funzione periodica corrisponde al numero che soddisfa la seguente proprietà:

\[f(x+P) = f(x)\]

per tutti i valori di \(x\). Si osservi che non tutte le funzioni hanno un punto. Quelli che lo fanno sono chiamati funzioni periodiche .

Periodo di alcune funzioni comuni

Le funzioni trigonometriche sono esempi di funzioni periodiche. Ad esempio, se consideriamo la funzione \(f(x) = \sin x\), il suo periodo è \(2\pi\), come mostrato nel grafico seguente:

Per \(\cos x\) abbiamo anche il periodo \(2\pi\). Dai un'occhiata al grafico qui sotto:

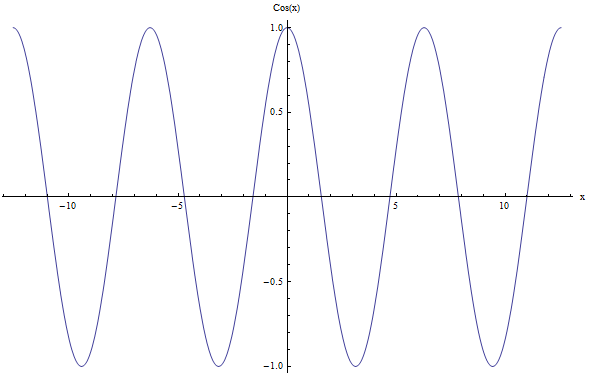
Periodo di altre funzioni trigonometriche

Ricorda che la funzione cosecante \(\csc x\) è l'inverso di \(\sin x\), questo è \(\csc x = \frac{1}{\sin x}\), quindi anche il periodo di \(\csc x\) è \(2\pi\).

Allo stesso modo, la funzione secante \(\sec x\) è l'inverso di \(\cos x\), questo è \(\sec x = \frac{1}{\cos x}\), quindi anche il periodo di \(\sec x\) è \(2\pi\).

E la tangente? La funzione tangente \(\tan x\) è leggermente diversa perché il suo periodo è \(\pi\). In effetti, il suo grafico sembra diverso da quelli del seno e del coseno, ma anche la tangente è periodica. Una differenza è che \(\tan x\) ha delle discontinuità. Controlla:

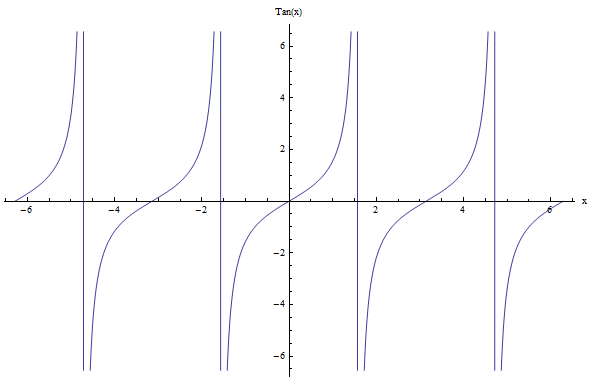
Analogamente a prima, la funzione cotangente \(\cot x\) è l'inverso di \(\tan x\), con \(\cot x = \frac{1}{\tan x}\), quindi anche il periodo di \(\cot x\) è \(\pi\).

Calcolo della frequenza

Un altro elemento importante da considerare per la funzione periodica è la frequenza (\(f\)), che viene calcolata in termini di periodo \(P\) come:

\[f = \frac{1}{P}\]

Quindi la frequenza è l'inverso del periodo. E viceversa, il periodo è l'inverso della frequenza.

Ad esempio, qual è la frequenza di \(\sin x\)? Seguendo la formula precedente, poiché sappiamo che per seno il periodo è \(P = 2\pi\):

\[f = \frac{1}{P} = \frac{1}{2\pi} \approx 0.1592\]

Questa calcolatrice calcolerà anche l'ampiezza, lo sfasamento e lo spostamento verticale se la funzione è definita correttamente. Questi parametri determinano piuttosto il comportamento della funzione trigonometrica.

Se hai bisogno di rappresentare graficamente una funzione trigonometrica, dovresti usare questo creatore di grafici trigonometrici .