Risolutori Algebra

Formula della pendenza

Istruzioni: Usa questa calcolatrice per calcolare la formula della pendenza, per due punti qualsiasi che fornisci, mostrando tutti i passaggi. Si prega di digitare due punti del modulo (x, y) nella casella del modulo sottostante.

Ulteriori informazioni sulla formula della pendenza

Questo Formula della pendenza calcolatrice ti permetterà di calcolare la pendenza per due punti dati della forma (x, y) utilizzando la formula ben nota, mostrando tutti i passaggi.

Devi fornire due punti della forma (x, y). Ad esempio, puoi fornire punti come (1/2, 1/3) o qualcosa che non è semplificato come (1/3+1/4, sqrt(8)).

Una volta forniti due punti validi della forma (x, y), il passaggio successivo consiste nel fare clic sul pulsante "Calcola" e ti verranno forniti tutti i passaggi del calcolo della formula della pendenza.

Il concetto di pendenza è cruciale in Algebra e Geometria, e la pendenza è molto importante per la costruzione di a funzione lineare .

Qual è la formula della pendenza?

Supponiamo di avere due punti \((x_1, y_1)\) e \((x_2, y_2)\) sul piano. Poi il Formula della pendenza è :

\[m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \]

Alcune persone diranno "è il rapporto tra la differenza in y e la differenza in x", con l'avvertenza che è necessario preservare l'ordine quando si fanno le differenze. Se in alto fai \(y_2 - y_1\), allora in basso fai \(x_2 - x_1\) e non \(x_1 - x_2\).

Inoltre, alcune persone chiamano questa formula di pendenza "Rise versus Run"/

Quali sono i passaggi per utilizzare la formula della pendenza

Passaggio 1: identificare i due punti dati. È una buona idea semplificare il più possibile le espressioni, prima di utilizzare la formula
Passaggio 2: determina qual è il primo punto e quale il secondo. La scelta è irrilevante per il risultato, a condizione che tu rimanga coerente con la tua scelta
Passaggio 3: utilizzare la formula \(b = \displaystyle \frac{y_2 - y_1}{x_2 - x_1}\) inserendo i valori del primo punto \(x_1\) e \(y_1\) e del secondo punto \(x_2\) e \(y_2\)
Passaggio 4: dopo aver inserito i valori, semplifica il più possibile per ridurre la pendenza alla sua forma più semplice

Il calcolo della pendenza utilizzando la formula è di solito un processo molto semplice, assicurati solo di mantenere coerente l'ordine dei punti.

Come utilizzare la pendenza?

La pendenza è una misura dell'inclinazione di una linea. Infatti, quando hai una funzione lineare della forma

\[y = m x + n\]

quindi la pendenza della linea è di m. Quanto sopra è noto come il forma dell'intercetta della pendenza di una linea.

Quali sono i passaggi per utilizzare la pendenza per una linea?

Step 1: Identificare la pendenza m. Semplificalo il più possibile
Passaggio 2: è necessario conoscere l'intercetta y, ovvero il punto nell'asse y in cui la linea lo attraversa e chiamarlo n
Passo 3: Quindi, l'equazione della retta è \(y = m x + n\)

Esistono altre forme per esprimere la linea oltre a Intercettazione del pendio . Tu hai il forma standard della linea , e il Forma punto-pendenza .

Come utilizzare la formula pendenza-intercetta

Quello è il centro di funzioni lineari (o affini lineari dovremmo dire) e grafici lineari. Infatti, quando hai la pendenza m e l'intercetta y n, calcoli direttamente l'equazione della retta come y = mx + n.

Geometricamente, è piuttosto semplice da interpretare, poiché l'intercetta y è assolutamente chiara come punto di intersezione tra la linea e l'asse y, e la pendenza è la misura dell'inclinazione. Come riferimento, una pendenza di m = 1 corrisponde a una pendenza di 45 ^o .

Al contrario, se ne hai funzione lineare , attraverso Semplificazione algebrica puoi sempre ridurre alla forma dell'intercetta pendenza y = mx + n, e quindi hai trovato la tua pendenza m e l'intercetta y n.

Esempio: utilizzo della formula della pendenza

Calcolare la pendenza per i seguenti punti: \(\displaystyle \left(\frac{1}{3}, \frac{5}{4}\right)\) e \(\displaystyle \left(\frac{7}{3}, \frac{7}{4}\right)\)

Soluzione: Dobbiamo calcolare la pendenza di una retta che passa per i punti \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) e \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\).

La seguente formula è necessaria per calcolare la pendenza dati i due punti:

\[m = \displaystyle\frac{y_2-y_1}{x_2-x_1}\]

Ora, collegando i valori dei punti \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) e \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\) si ottiene:

\( \displaystyle m = \frac{\frac{7}{4}-\frac{5}{4}}{\frac{7}{3}-\frac{1}{3}}\)

Grouping and operating all the integer terms and fractions: \(\displaystyle \frac{ 7}{ 4}-\frac{ 5}{ 4}=\frac{ 7-5}{ 4}=\frac{ 2}{ 4}=\frac{ 2}{ 2 \times 2}=\frac{ \cancel{ 2}}{ \cancel{ 2} \times 2}=\frac{ 1}{ 2}\) and \(\displaystyle \frac{ 7}{ 3}-\frac{ 1}{ 3}=\frac{ 7-1}{ 3}=\frac{ 6}{ 3}=\frac{ 3 \times 2}{ 3}=\frac{ \cancel{ 3} \times 2}{ \cancel{ 3}}=2\)

\( = \,\,\)

\(\displaystyle \frac{\frac{1}{2}}{2}\)

Grouping and operating all the integer terms and fractions: \(\displaystyle \frac{ 1}{ 2} \times \frac{ 1}{ 2}=\frac{ 1}{ 2 \times 2}=\frac{ 1}{ 4}\)

\( = \,\,\)

\(\displaystyle \frac{1}{4}\)

Quindi, concludiamo che la pendenza di una retta che passa per i punti \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) e \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\) è \(m = \displaystyle \frac{1}{4}\).

Esempio: altri esempi della formula della pendenza

Usa la formula della pendenza per trovare la pendenza della retta che passa per i punti: \((2, 4)\) e \((5, 12)\)

Soluzione: In questo caso abbiamo i punti \(\displaystyle (x_1, y_1) = \left(2,4\right)\) e \(\displaystyle (x_2, y_2) = \left(5,12\right)\), che sono i punti attraverso i quali sappiamo che passa la linea.

La formula della pendenza è:

\[m = \displaystyle\frac{y_2-y_1}{x_2-x_1}\]

Ora, collegando i valori dei punti \(\displaystyle (x_1, y_1) = \left(2,4\right)\) e \(\displaystyle (x_2, y_2) = \left(5,12\right)\) si ottiene:

\(\displaystyle m = \frac{12-4}{5-2}\)

\( = \)

\(\displaystyle \frac{8}{3}\)

Reducing the integers that can be subtracted together: \(\displaystyle 12-4 = 8\), \(\displaystyle 5-2 = 3\)

Quindi, concludiamo che la pendenza di una retta che passa per i punti \(\displaystyle (x_1, y_1) = \left(2,4\right)\) e \(\displaystyle (x_2, y_2) = \left(5,12\right)\) è \(m = \displaystyle \frac{8}{3}\).

Esempio: forma pendenza-intercetta

Trova la forma dell'intercetta della pendenza per la seguente linea: \(2x + 4y = 3 + \frac{1}{2}x\).

Soluzione: Abbiamo la seguente equazione:

\[\displaystyle 2x+4y=3+\frac{1}{2}x\]

Ponendo \(y\) sul lato sinistro e \(x\) e la costante sul lato destro otteniamo

\[\displaystyle 4y = \left(\frac{1}{2}-2\right)x +3\]

Ora, il termine moltiplicando \(y\) è \( 4 - 0 = 4\), e poichè \( \frac{1}{2} - 2 = -\frac{3}{2}\) si ottiene quanto segue

\[\displaystyle 4y=-\frac{3}{2}x+3\]

Ora, risolvendo per \(y\), dividendo entrambi i lati dell'equazione per \(4\), si ottiene quanto segue

\[\displaystyle y=-\frac{\frac{3}{2}}{4}x+\frac{3}{4}\]

e semplificando si ottiene la seguente formula

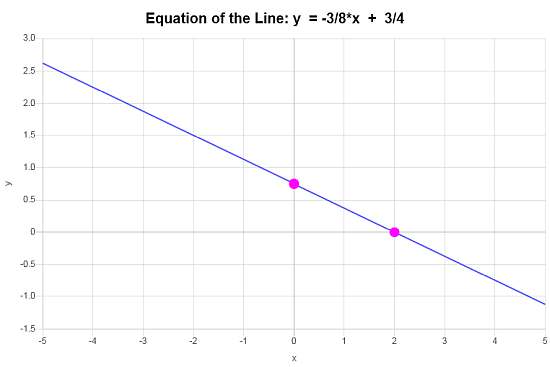
\[\displaystyle y=-\frac{3}{8}x+\frac{3}{4}\]

Conclusione : Sulla base dei dati forniti, concludiamo che l'equazione della retta in forma di intercetta pendenza è \(\displaystyle y=-\frac{3}{8}x+\frac{3}{4}\), con una pendenza di \(\displaystyle b = -\frac{3}{8}\) e y-intercetta di \(\displaystyle n = \frac{3}{4}\).

Graficamente, la linea è simile a:

Altri calcolatori di funzioni lineari

Insieme a funzioni quadratiche , le funzioni lineari sono tra gli oggetti più importanti in Math. puoi calcolare la pendenza di una retta, trovare la linea perpendicolare , e convertire la linea tra diverse forme, a seconda delle esigenze.

Una cosa notevole per le funzioni lineari è che è più facile da trovare funzioni lineari inverse , poiché la maggior parte delle funzioni lineari sono 1 a 1 (ad eccezione delle linee orizzontali).