Come utilizzare la calcolatrice di pendenza con i passaggi

Utilizzate questa calcolatrice per trovare la pendenza di una retta da voi fornita, con tutti i passaggi indicati.

La pendenza è una misura dell'inclinazione della retta rispetto agli assi coordinati. Una pendenza positiva indica che la retta ha un'inclinazione verso l'alto, mentre una pendenza negativa indica che la retta ha un'inclinazione verso il basso.

Una pendenza pari a zero indica che la linea è orizzontale, mentre una linea verticale non ha una pendenza ben definita.

Come calcolare una pendenza?

Normalmente il calcolo della pendenza è semplice, ma esistono diversi modi per calcolarla e tutto dipende da quali informazioni vengono fornite e da come vengono fornite.

Il modo più comune in cui viene presentato il calcolo della pendenza è fornendo prima un'equazione lineare per la quale è necessario trovare la sua pendenza o fornendo due punti attraversati da una linea.

Calcolatrice pendenza dall'equazione: trovare la pendenza della linea

Questa calcolatrice ti mostrerà come calcolare la pendenza di una linea che fornisci e avrai diversi modi per indicare e definire la tua linea. Ti darà anche un grafico che riflette la pendenza calcolata.

Ad esempio, un modo comune è quello di definire la retta fornendo un'equazione, e poi questa calcolatrice calcolerà la pendenza dall'equazione.

La strategia generale consiste nel mettere l'equazione della retta in forma di intercetta della pendenza , da cui è facile riconoscere la pendenza dalla struttura dell'equazione \(y = mx + n\).

Anche questo è un calcolatore di pendenza da due punti

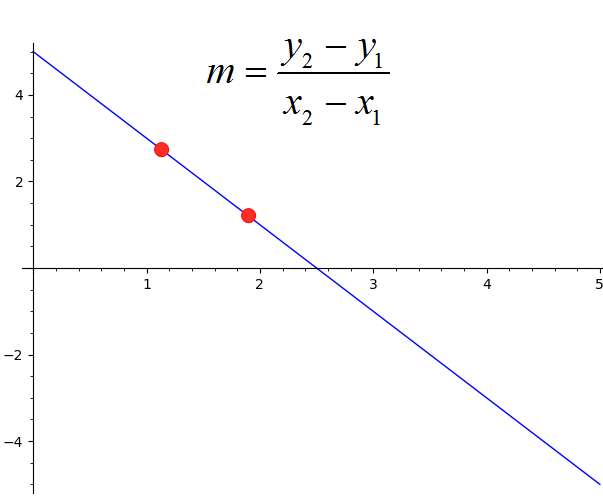
Forse uno dei modi più comuni per calcolare la pendenza è quando si definire l'equazione fornendo due punti come \((x_1, y_1)\), \((x_2, y_2)\). Quindi, come trovi la pendenza da due punti? La pendenza viene semplicemente calcolata come

\[m = \frac{y_2-y_1}{x_2-x_1}\]

che è come trovare la pendenza da due punti. Non dimentichiamo che questi due punti sono di solito punti in cui passa una linea, quindi stai trovando la pendenza della linea che passa attraverso quei punti.

In definitiva, il modo in cui trovare la pendenza di una retta dipende da come viene definita la retta stessa. Questa calcolatrice vi aiuterà in tutti i casi, anche quando nel calcolo sono presenti frazioni.

Interpretazione: cos'è una pendenza del 2%?

Esistono diversi modi per vederlo, ma un modo comune è pensare che per ogni aumento di 100 unità in X, la linea aumenta di 2 unità in Y, il che spiega 2/100 = 0,02 = 2%.

Sulla stessa linea interpretativa, si può dire che una pendenza del 45% è tale che un aumento di 100 unità in X porta ad un aumento di 45 unità in Y. Si noti che questa NON è la stessa cosa di una pendenza con 45 ^O gradi.

Calcolatore di pendenza istantaneo

L'idea di un calcolatore di pendenza è semplice quando si considerano due punti, nel qual caso si utilizza la formula sopra. Ma qual è la pendenza istantanea? Ciò si riferisce alla pendenza quando i due punti diventano sempre più vicini.

Quindi vuoi vedere a quale valore si avvicina anche la pendenza, quando i due punti si avvicinano insieme. L'idea della pendenza istantanea si riflette in questo calcolatore derivato , che essenzialmente calcola le pendenze istantanee.

Esempio: calcolo della pendenza

Supponiamo di avere una riga che ha la seguente forma standard \( \frac{3}{4} x + 2y = 6\). Trova la pendenza della retta.

Soluzione: Calcolo della pendenza di una retta

Ci è stata fornita la seguente equazione:

\[\displaystyle \frac{3}{4}x+2y=6\]

Mettendo \(y\) sul lato sinistro e \(x\) e la costante sul lato destro otteniamo

\[\displaystyle 2y = -\frac{3}{4}x +6\]

Ora, risolvendo per \(y\), dividendo entrambi i membri dell'equazione per \(2\), si ottiene quanto segue

\[\displaystyle y=-\frac{\frac{3}{4}}{2}x+\frac{6}{2}\]

e semplificando si ottiene la seguente formula

\[\displaystyle y=-\frac{3}{8}x+3\]

Conclusione : Sulla base dei dati forniti, concludiamo che la pendenza della linea è \(\displaystyle m = -\frac{3}{8}\).

Esempio: calcolo della pendenza da due punti

Supponiamo di avere una linea che passa per 2 punti: \( (1, 2)\) e \( (4, 11/3)\). Trova la pendenza della retta.

Soluzione:

Calcolo della pendenza di una retta

L'informazione fornita sulla linea è che la linea passa per i punti\(\displaystyle \left( 1, 2\right)\) e \(\displaystyle \left( 4, \frac{11}{3}\right)\)

Pertanto il primo passo consiste nel calcolare la pendenza. La formula per la pendenza è: \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} \]

Ora, inserendo i numeri corrispondenti is , otteniamo che la pendenza è: \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ \displaystyle \frac{11}{3} - 2}{ \displaystyle 4 - 1} = \frac{ \displaystyle \frac{11}{3}-2}{ \displaystyle 4-1} = \frac{5}{9}\]

Troviamo allora che la pendenza è \(\displaystyle m = \frac{5}{9}\) e che la retta passa per il punto \(\displaystyle \left( 1, 2\right)\)

Conclusione : Sulla base dei dati forniti, concludiamo che la pendenza della linea è \(\displaystyle m = \frac{5}{9}\).

La pendenza di una retta è una delle sue proprietà più importanti, insieme alla pendenza della linea Intercettazioni a Y E intercetta x perché definiscono essenzialmente la linea.