Calcolatore della forma della linea punto-pendenza
Istruzioni: Usa questa calcolatrice per trovare la forma di intercettazione della pendenza della linea che fornisci, con tutti i passaggi mostrati. A tal fine, è necessario fornire alcune informazioni sulla linea che si desidera inserire in forma di pendenza puntuale.
Ci sono diversi modi in cui puoi parlarci della tua linea. Puoi fornire: (1) sia la pendenza che l'intercetta y, (2) puoi digitare qualsiasi equazione lineare (es: \(x + 3y = 2 + \frac{2}{3}x\)), (3) puoi indicare la pendenza e un punto che la retta passa attraverso, oppure (4) puoi indicare due punti in cui passa la linea.
A proposito di questo calcolatore di forma punto-pendenza della linea.
Questo calcolatore dell'equazione punto-pendenza ti fornirà un calcolo passo-passo dell'equazione della linea in forma punto-pendenza per qualsiasi linea che hai inizialmente fornito.
Quello che devi fare è identificare la linea con cui vuoi lavorare. Questa riga può essere identificata in molti diversi e la selezionerai in base alle informazioni che hai fornito.
Uno dei modi più comuni è definire una linea fornendo la sua pendenza e la sua Intercettazioni a Y , ma non è certo l'unico modo.
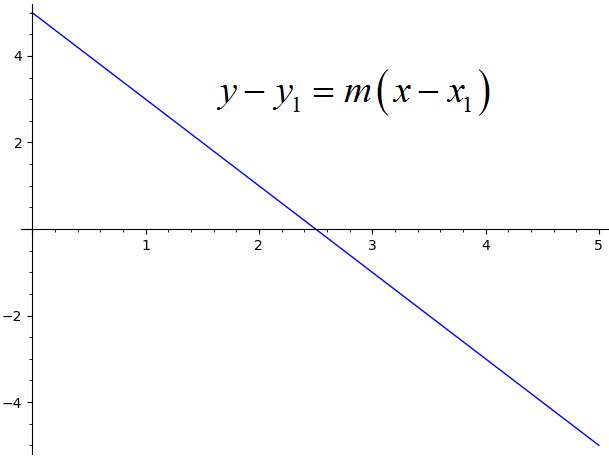
Come rappresentare una linea in forma punto-pendenza?
Una retta si dice in forma di pendenza se può essere scritta come:
\[y - y_1= m (x -x_1)\]In questo contesto, \(m\) è identificato come la pendenza della linea e \((x_1, y_1)\) è un punto attraverso il quale passa la linea.
Come puoi trovare l'intercettazione del punto con una calcolatrice?
Se ti capita di conoscere la pendenza \(m\) della linea e un punto \((x_1, y_1)\) in cui la linea è passata, il processo è facile e diretto, ma potrebbe essere più complicato se la linea è definita usando un altro tipo di informazione.
Perché è utile la forma punto-pendenza di una linea
La forma punto-pendenza è utile perché fornisce un'interpretazione diretta del pendenza della retta come il tasso di cambiamento. Infatti, direttamente dalla forma punto-pendenza otteniamo
\[\frac{y-y_1}{x-x_1} = m\]Posso ottenere la forma della pendenza del punto con due punti?
Sì! Se hai due punti, li usi prima per calcolare la pendenza \(m\) e poi scegli uno qualsiasi dei punti per applicare direttamente la formula
\[y - y_1= m (x -x_1)\]
Esempio: calcolo del modulo punto-pendenza
Supponiamo di sapere che la linea passa per i punti \(( \frac{1}{3}, 2)\) e \((\frac{7}{2}, 3)\). Trova la forma punto-pendenza della retta.
Risposta:
L'informazione fornita sulla retta è che essa passa per i punti\(\displaystyle \left( \frac{1}{3}, 2\right)\) e \(\displaystyle \left( \frac{7}{2}, 3\right)\)
Pertanto, il primo passo consiste nel calcolare la pendenza. La formula per la pendenza è: \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} \]
Ora, inserendo i numeri corrispondenti in , otteniamo che la pendenza è: \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ \displaystyle 3 - 2}{ \displaystyle \frac{7}{2} - \frac{1}{3}} = \frac{ \displaystyle 1}{ \displaystyle \frac{19}{6}} = \frac{6}{19}\]
Ora sappiamo che la pendenza è \(\displaystyle m = \frac{6}{19}\) e che la retta passa per il punto \(\displaystyle \left( \frac{1}{3}, 2\right)\)
Quindi, con le informazioni in nostro possesso, possiamo costruire direttamente la forma punto-pendenza della retta, che è
\[\displaystyle y - y_1 = m \left(x - x_1\right)\]e poi inserendo i valori noti di \(\displaystyle m = \frac{6}{19}\) e \(\displaystyle \left( x_1, y_1 \right) = \left( \frac{1}{3}, 2\right)\), si ottiene che
\[\displaystyle y-2 = \frac{6}{19} \left(x-\frac{1}{3}\right)\]Conclusione : Sulla base dei dati forniti, concludiamo che l'equazione della retta in forma punto-pendenza è \(\displaystyle y-2=\frac{6}{19}\left(x-\frac{1}{3}\right) \).
Puoi anche utilizzare il nostro Calcolatrice di moduli standard e calcolatrice per l'intercettazione della pendenza di una riga, se quelli sono invece i formati che ti interessano.




