Maggiori informazioni su questa equazione di linea nella calcolatrice in forma standard

Questa equazione della linea nel calcolatore di equazioni in forma standard ti consentirà di definire un'equazione in uno dei quattro modi che preferisci e ti mostrerà tutti i passaggi richiesti.

Come trovare l'equazione di una retta? Quindi la prima cosa è definire un'equazione lineare. A tale scopo, puoi fornire un'equazione direttamente o in altro modo, a seconda delle informazioni che hai a disposizione, puoi fornire:

(1) la pendenza e l'intercetta y.

Oppure (2) la pendenza e un punto in cui passa la linea,

oppure (3) puoi fornire due punti in cui passa la linea.

Il modo in cui utilizzerai per definire la tua equazione dipenderà dalle informazioni che hai a disposizione.

Qual è il formato di un'equazione lineare in forma standard?

Un'equazione lineare si dice in forma standard se ha la seguente struttura:

\[a x + by = c\]

Quindi, il tuo obiettivo è determinare la formula della forma standard e trovare le costanti a, b e c che la determinano.

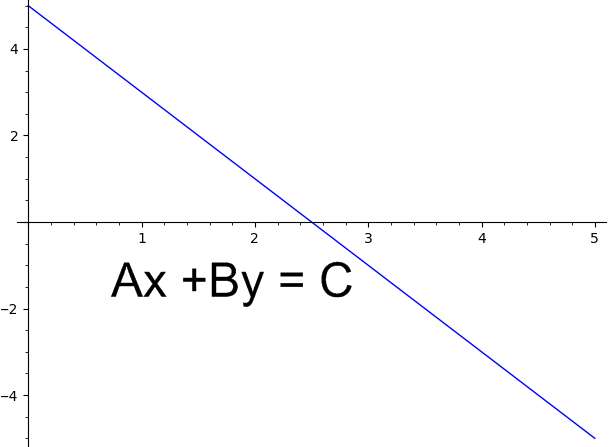
Come si risolve il modulo standard su una calcolatrice?

Con questo calcolatore, tutto ciò che devi fare è fornire informazioni per definire l'equazione, tra le quattro diverse opzioni.

Perché è necessario il modulo standard

Alcune forme specifiche di un'equazione provengono dalla tradizione, ma di solito perché è utile utilizzare una forma specifica.

Nel caso del modulo standard, è pratico averlo nella forma \(a x + by = c\), perché collegando \(x=0\) è facile calcolare il Intercettazioni a Y , e collegando \(y=0\) è facile calcolare il intercetta x .

Inoltre, il modulo standard è comunemente usato come formato preferito durante la risoluzione sistemi simultanei di equazioni lineari .

Questo risolutore può gestire equazioni lineari frazionarie?

Una delle cose belle di questa calcolatrice è che tutti i coefficienti che usi per definire l'equazione possono essere qualsiasi espressione numerica generica , che include frazioni .

Per vedere un esempio di come questa calcolatrice gestisce le equazioni lineari frazionarie, controlla l'esempio seguente.

Esempio: Calcolo dell'equazione di una retta

Supponiamo di avere una retta che passa per il punto \(\left( \frac{1}{3}, \frac{2}{3}\right)\) con pendenza \(m = \frac{1}{2}\). Trova la forma standard della linea.

Risposta:

L'informazione inizialmente fornita sulla linea è che la pendenza è \(\displaystyle m = \frac{1}{2}\) e la linea passa per il punto \(\displaystyle \left( \frac{1}{3}, \frac{2}{3}\right)\)

Quindi, con le informazioni che abbiamo, possiamo costruire direttamente il forma punto-pendenza della linea , che è

\[\displaystyle y - y_1 = m \left(x - x_1\right)\]

e poi inserendo i valori noti di \(\displaystyle m = \frac{1}{2}\) e \(\displaystyle \left( x_1, y_1 \right) = \left( \frac{1}{3}, \frac{2}{3}\right)\), si ottiene che

\[\displaystyle y-\frac{2}{3} = \frac{1}{2} \left(x-\frac{1}{3}\right)\]

Ora, dobbiamo espandere il lato destro dell'equazione distribuendo la pendenza, in modo da ottenere \[\displaystyle y = \frac{1}{2} x + \frac{1}{2} \left(-\frac{1}{3}\right) + \frac{2}{3}\]

e semplificando si ottiene che \[\displaystyle y=\frac{1}{2}x+\frac{1}{2}\]

Passando la variabile indipendente al lato sinistro dell'equazione si ottiene la seguente forma standard della linea:

\[\displaystyle -\frac{1}{2}x+y=\frac{1}{2}\]

Conclusione : Sulla base dei dati forniti, concludiamo che l'equazione della retta in forma standard è \(\displaystyle -\frac{1}{2}x+y=\frac{1}{2}\).

Altri utili calcolatori relativi alle funzioni lineari

Spesso, vuoi solo dare una rapida occhiata a come appaiono le cose graficamente, per cui potresti usare questo strumento rappresentare graficamente equazioni lineari

Oppure puoi anche rappresentare graficamente due equazioni lineari e trova l'intersezione di due rette , se esiste.

Come passaggio precedente, potresti voler calcolare prima la pendenza, quindi a te il modulo di intercettazione della pendenza, per il quale potresti usare questo calcolatrice della formula della pendenza di una linea .