Ulteriori informazioni sui derivati trigonometrici

Usa questa calcolatrice per trovare le derivate trigonometriche, che in questo caso assumiamo essere qualsiasi funzione differenziabile valida che coinvolge una o più funzioni trigonometriche elementari.

Un esempio di una funzione valida per questa calcolatrice è f(x) = sin(x)/x, o f(x) = x*sin(x^3), giusto per fare un esempio.

Dopodiché, quando avrai già digitato la funzione corrispondente, potrai poi cliccare sul pulsante "Calcola", così da avere tutti i passi del calcolo della derivata che ti vengono mostrati.

Le funzioni trigonometriche giocano un ruolo cruciale nel calcolo, così come in calcolo delle derivate generalmente. In definitiva, le funzioni più complesse possono ridurre le loro derivate al calcolo della derivata per funzioni trigonometriche più semplici.

Derivati di trigonometria di base

L'idea di utilizzare le regole derivate è quella di scomporre una funzione complessa e differenziarla utilizzando le derivate di funzioni note. Nello specifico, semplici funzioni trigonometriche come seno, coseno, tangente e cotangente giocheranno un ruolo importante in questo.

Quali sono le derivate trigonometriche di base?

• Derivata Trigonometrica 1: $\frac{d}{dx} \sin (x) = \cos(x)$
• Trigonometria Derivata 2: $\frac{d}{dx} \cos (x) = -\sin(x)$
• Derivata Trigonometrica 3: $\frac{d}{dx} \tan (x) = \sec^2(x)$
• Derivata Trigonometrica 4: $\frac{d}{dx} \cot (x) = -\csc^2(x)$
• Derivata Trigonometrica 5: $\frac{d}{dx} \sec (x) = \sec(x)\tan(x)$
• Derivata Trigonometrica 6: $\frac{d}{dx} \sec (x) = -\csc(x)\cot(x)$

Queste sono le derivate di base che devi conoscere molto, e possibilmente memorizzare per poterle usare Regole derivate calcolare derivate più complicate

Le derivate trigonometriche sono in gradi?

No, ci sono le derivate delle funzioni trigonometriche radianti , quindi le derivate trigonometriche trovate riflettono il fatto che l'argomento x è misurato in radianti.

Quindi, per esempio, supponiamo di voler calcolare la derivata di sin in gradi , quindi definiamo $f(y) = \sin(y)$, dove $y$ è misurato in gradi.

Ora, sia $x = \frac{\pi y}{180}$ l'angolo equivalente in radianti e anche risolvendo per $y$ troviamo che $y = \frac{180 x}{\pi}$, quindi usando la regola della catena:

$$\displaystyle \frac{d}{dy} f(y) = \displaystyle \frac{d}{dy} f(y(x)) \frac{dy}{dx} = \frac{180}{\pi} \cos(y)$$

Quindi, basandoci su questo, la derivata del seno in gradi è effettivamente coseno in gradi, ma moltiplicato per un fattore $\frac{180}{\pi}$.

Come si trovano le derivate in trigonometria?

I derivati trigonometrici si trovano per definizione, utilizzando le identità trigonometriche di base. Ad esempio, utilizzando il seno della formula della somma possiamo derivare la derivata di $\sin(x)$, usando la definizione di limite:

$$\displaystyle \frac{d}{dx} \sin(x) = \displaystyle \lim_{h \to 0} \frac{\sin(x+h)-\sin(x)}{h}$$ $$\displaystyle = \displaystyle \lim_{h \to 0} \frac{\sin(x)\cos(h) + \cos(x)\sin(h) - \sin(x)}{h}$$ $$\displaystyle = \displaystyle \lim_{h \to 0} \frac{\sin(x)(\cos(h)-1) + \cos(x)\sin(h)}{h}$$ $$\displaystyle = \displaystyle \lim_{h \to 0}\left( \frac{\sin(x)(\cos(h)-1)}{h} + \frac{\cos(x)\sin(h)}{h} \right)$$ $$\displaystyle = \displaystyle \lim_{h \to 0}\left( \frac{\sin(x)(\cos(h)-1)}{h} \right)+ \displaystyle \lim_{h \to 0}\left( \frac{\cos(x)\sin(h)}{h} \right)$$ $$\displaystyle = \sin(x) \displaystyle \lim_{h \to 0} \left( \frac{(\cos(h)-1)}{h} \right)+ \cos(x) \displaystyle \lim_{h \to 0}\left( \frac{\cos(x)\sin(h)}{h} \right)$$ $$\displaystyle = \sin(x) \cdot 0 + \cos(x) \cdot 1 = \cos(x)$$

Suggerimenti e trucchi

La cosa principale da asporto per te è ricordare sempre ciò che il 6 derivati trigonometrici sono , e conoscili a memoria, poiché li utilizzerai continuamente, insieme a quelli di base regole di differenziazione .

Allo stesso modo, puoi utilizzare le identità trigonometriche e la definizione di funzione inversa per trovare le derivate trigonometriche inverse più comuni.

Esempio: calcolo della derivata trigonometrica

Si consideri la seguente funzione: $f(x) = \sin^2(x)+ \frac{1}{x}$. Trova la sua derivata

Soluzione: I derivati trigonometrici coinvolgono la funzione trigonometrica che deve essere differenziata. Considera la funzione $\displaystyle f(x)=\sin\left(x\right)^2+\frac{1}{x}$, che contiene una funzione seno, quindi si qualifica come derivata trigonometrica.

Risultati : Per questo esempio, si trova che la derivata è:

$$f'(x) = \frac{2x^2\cos\left(x\right)\sin\left(x\right)-1}{x^2}$$

È molto utile rappresentare la funzione e la sua derivata su un grafico. Vedi sotto:

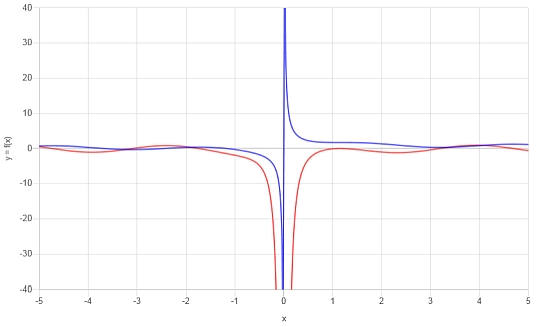
Esempio la derivata di una funzione trigonometrica

Considera la seguente funzione trigonometrica: $f(x) = \sin(x) + x \cos(x)$, trova la sua derivata.

Soluzione: Ora dobbiamo lavorare con la derivata della seguente funzione trigonometrica $\displaystyle f(x)=\sin\left(x\right)+x\cos\left(x\right)$.

Conclusione Finale : Concludiamo che la derivata è data da:

$$f'(x) = -x\sin\left(x\right)+2\cos\left(x\right)$$

Si ottiene il seguente grafico:

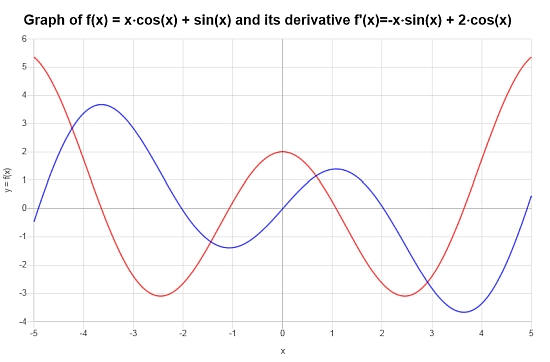
Esempio: derivate trigonometriche e differenziazione implicita

Trova $\frac{dy}{dx}$ per $\sin(x)+\cos(y) = 1$.

Soluzione: Abbiamo bisogno di usare Differenziazione implicita , quindi distinguiamo entrambi i lati e usiamo the Regola Di Derivazione :

$$\frac{dy}{dx}\left(\sin(x)+\cos(y)\right) = \frac{dy}{dx} \left(1\right)$$ $$\Rightarrow \cos(x)-\sin(y)y' = 0$$ $$\Rightarrow \sin(y)y' = \cos(x)$$ $$\Rightarrow y' = \frac{\cos(x)}{\sin(y)}$$

che conclude il calcolo.

Altri utili calcolatori derivati

trovare la derivata di funzioni semplici ed elementari è la pietra angolare del processo di ricerca delle derivate di funzioni più complicate, attraverso l'uso del ben noto regole di differenziazione .

In questo contesto, di base funzioni trigonometriche possono essere considerate funzioni elementari per le quali la derivata può essere calcolata utilizzando i limiti, tramite la sua stessa definizione. Tra le funzioni elementari più utili abbiamo polinomio e funzioni razionali.