Maggiori informazioni su questo calcolatore di trigonometria

Questo calcolatore trigonometrico ti permetterà di valutare qualsiasi espressione trigonometrica che fornisci. Assicurati di fornire un'espressione trigonometrica valida, può essere qualcosa di diretto come cos(pi/2), o potrebbe essere qualcosa che non è completamente semplificato, come sin(1/3*pi+3/4*pi).

Puoi anche fornire una funzione trigonometrica come sin(1/3*pi x +3/4*pi + x) e questa calcolatrice analizzerà e, se possibile, fornirà il periodo, la frequenza, ecc. corrispondenti, insieme alla sua grafico .

Una volta fornita un'espressione trigonometrica valida, tutto ciò che devi fare è cliccare su "Calcola" e ti verranno mostrati tutti i passaggi del calcolo.

espressioni trigonometriche sono abbastanza necessari, specialmente quando lo sei risolvere triangoli . Di solito è semplice ridurre qualsiasi calcolo trigonometrico al calcolo di alcuni angoli notevoli per il coseno e il loro .

Come fare i calcoli trigonometrici?

Fare un calcolo trigonometrico può essere un'attività molto generale e ampia, che può avere strategie specifiche che funzionano meglio a seconda del calcolo specifico del trigonometrico che devi eseguire e delle funzioni trigonometriche coinvolte, ma ci sono alcune strategie generali che possono esserti utili.

Quali sono i passaggi per un calcolo trigonometrico

• Passaggio 1: identificare chiaramente l'espressione trigonometrica che si desidera calcolare e semplificare i numeri e le frazioni il più possibile. Ad esempio, se hai cos(1+1/2), noterai prima che 1+1/2 = 3/2, quindi hai effettivamente bisogno di cos(3/2)
• Passaggio 2: una volta raggruppate e gestite le possibili frazioni e i numeri semplici, se possibile, determinare se esistono funzioni trigonometriche diverse da seno e coseno. Se ci sono, esprimi tutto in termini di seno e coseno
• Passaggio 3: ora passa attraverso tutte le parti, che ora coinvolgono solo seno e coseno , e valutare se ci sono angoli notevoli che coinvolgono multipli o frazioni di π
• Passaggio 4: valutare direttamente quelle espressioni con notevole angoli che può essere semplificato. Quelli che non possono essere semplificati direttamente (se ce ne sono) lasciano così com'è o forniscono un ( valore arrotondato ) di loro

È consuetudine lasciare così come sono espressioni che non hanno conosciuto, semplici semplificazioni. Ad esempio, cos(1/4) non ha riduzione semplice, quindi viene generalmente lasciato così com'è. Ma per esempio, cos(π/3) = 1/2, quindi tali semplici riduzioni sono ovviamente eseguite

Calcolatrice di trigonometria con passaggi

Il vantaggio di questa calcolatrice è che ti mostrerà tutti i passaggi rilevanti del processo. Il processo è semplice: si tratta espressioni semplificative che coinvolgono solo numeri, frazioni ed espressioni numeriche complessivamente valutabili direttamente.

Quindi, e solo allora, dovresti eseguire il calcolo del trigonometro, in modo da chiarire le cose il più possibile prima di tentare qualsiasi calcolo del trigonometro.

Vantaggi dell'utilizzo di un'app calcolatrice trigonometrica

Potresti pensare, vabbè, conosco abbastanza bene le mie funzioni trigonometriche per gli angoli notevoli di base, quindi non ho bisogno di un'app calcolatrice trigonometrica. Potrebbe benissimo essere così, anche se potresti esitare un po' ti viene presentato qualcosa come \(\sin\left(\displaystyle\frac{345}{11}\pi\right)\)....puoi semplificarlo? È un angolo notevole?

È davvero una buona cosa cercare di risolvere le cose a mano, ed esercitando la tua memoria trigonometrica, ma a app calcolatrice trigonometrica può aiutarti almeno a controllare le tue risposte.

Esempio: calcolo del trigonometro

Calcolare l'espressione trigonometrica: \(\sin\left(\frac{5}{4}\pi\right)\)

Soluzione: È stata fornita la seguente espressione trigonometrica da calcolare:

\[ \sin\left(\frac{5\pi}{4}\right)\]

Ispezionando la data espressione trigonometrica, possiamo trovare un angolo notevole, che è \(\sin\left(\frac{5\pi{}}{4}\right)\).

▹ Per l'angolo \(\frac{5\pi{}}{4}\) si ottiene graficamente:

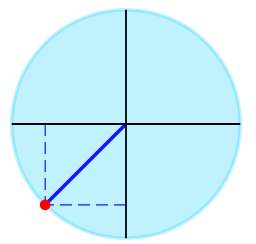
L'espressione trigonometrica data può essere semplificata come:

Conclusione: Concludiamo che \(\displaystyle \sin\left(\frac{5\pi}{4}\right) = -\frac{1}{2}\sqrt{2} \approx -0.7071\).

Esempio: utilizzo del calcolatore trigonometrico

Ridurre : \(\displaystyle \cos\left(\frac{1}{3} + \frac{5}{4}\right)\)

Soluzione: Ora dobbiamo lavorare su:

\[ \cos\left(\frac{1}{3}+\frac{5}{4}\right)\]

Questo termine trigonometrico può essere semplificato come segue:

Conclusione: Si conclude che \(\displaystyle \cos\left(\frac{1}{3}+\frac{5}{4}\right) = \cos\left(\frac{19}{12}\right) \approx -0.0125\).

Esempio: semplificazione trigonometrica

Calcola \( \sin\left(\frac{2}{3} \times \frac{6}{5} \pi\right)+ \frac{2}{5}\cdot \cos(\frac{\pi}{4}) \).

Soluzione: Ispezionando la data espressione trigonometrica, possiamo trovare un angolo notevole, che è \(\cos\left(\frac{\pi{}}{4}\right)\).

▹ Per l'angolo \(\frac{\pi{}}{4}\) si ottiene graficamente:

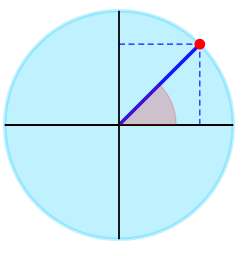
L'espressione trigonometrica data può essere semplificata come:

Conclusione: Concludiamo che \(\displaystyle \sin\left(\frac{2}{3}\cdot\frac{6}{5}\pi\right)+\frac{2}{5}\cos\left(\frac{\pi}{4}\right) = \frac{1}{5}\sqrt{2}+\frac{1}{4}\sqrt{-2\sqrt{5}+10} \approx 0.8706\).

Altri calcolatori di geometria

Lavorare con le funzioni trigonometriche è strettamente correlato al lavorare con i triangoli, quindi quando si lavora con a calcolatrice triangolare troverai molti calcoli trigonometrici.