Calcolatore differenziale
Istruzioni: Usa questo calcolatore differenziale, per trovare il differenziale di una funzione che fornisci, in un dato punto che fornisci, mostrando tutti i passaggi. Si prega di digitare la funzione e il punto nella casella del modulo sottostante.
Calcolatore differenziale
Questa calcolatrice ti permetterà di calcolare il differenziale di una funzione che fornisci, in un punto che fornisci, mostrando tutti i passaggi del processo.
La funzione che fornisci può essere qualsiasi funzione differenziabile valida come f(x) = x^2 + 2x o f(x) = x^2*sin(x), solo per citare due esempi.
Quindi, una volta fornita la funzione e il punto per il calcolo del differenziale, basta cliccare su "Calcola" per avere tutti i passaggi del processo mostrato.
L'idea di Differenziale è strettamente con quello della linea tangente e Approssimazione Lineare , poiché il differenziale misura precisamente la variazione di y, lungo il Linea tangente al punto dato.
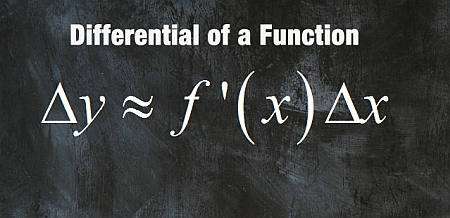
Cos'è un differenziale?
Nel calcolo differenziale, l'idea è che le derivate forniscano informazioni sulla velocità di variazione istantanea di una funzione in un dato punto.
Il concetto di differenziale utilizza il tasso di cambio determinato dalla derivata in un dato punto \(x_0\) per approssimare il comportamento della funzione con il suo Linea tangente .
La formula del differenziale si basa sull'idea che
\[\displaystyle \Delta y \approx f'(x_0) \Delta x \]dove \(\Delta y = y - f(x_0)\) e \(\Delta x = x - x_0\). Per il differenziale \(dy\), definiamo
\[\displaystyle dy = f'(x_0) dx \]Questa definizione (libera) si basa sull'idea che l'approssimazione lineare e la funzione si avvicinino allo stesso comportamento quando \(x\) è sufficientemente vicino a \(x_0\).
Passi per il calcolo di un differenziale
- Fase 1: Identifica la funzione f(x) e il punto x0 in cui vuoi calcolare il differenziale
- Passo 2: Calcola la derivata f'(x) e valutala in x0, quindi ottieni f'(x0). Semplificalo, se necessario
- Smusso 3: Usa la formula \(\displaystyle dy = f'(x_0) dx \)
A volte troverai il differenziale scritto come \(\displaystyle \Delta y = f'(x_0) \Delta x = f'(x_0)(x-x_0) \), come una forma per indicare che utilizzerai il differenziale per stimare i cambiamenti in y, misurati da \(\Delta y\).
Calcolatrice differenziale dy
Usare un calcolatore differenziale può farti risparmiare tempo con il processo di calcolo della derivata. L'idea del differenziale è sempre stata strana, nel senso che sembra essere definita in modo impreciso.
Sebbene esista un modo per definire formalmente i differenziali e le loro operazioni (un argomento chiamato Forme differenziali), la maggior parte dei matematici non vede una ragione per l'esistenza dei differenziali, poiché non forniscono alcuna nuova informazione che la derivata o l'approssimazione del primo ordine non fornire.
Interpretazione differenziale totale
L'applicazione e l'interpretazione più comune del differenziale è quando viene utilizzato nella sua espressione "finita":
\[\displaystyle \Delta y = f'(x_0) \Delta x = f'(x_0)(x-x_0) \]dove stai cercando di stimare la variazione in y, misurata da \(\Delta y\), dalla variazione in x, misurata da \(\Delta x\) e la derivata nel punto.
A volte questo \(\Delta y\) è chiamato il variazione totale o differenziale totale .
Suggerimenti e trucchi
Non dimentichiamo che il differenziale può essere assunto come definizione teorica, \(\displaystyle dy = f'(x_0) dx \), che indica la variazione infinitesimale di y causata da una variazione infinitesimale di x.
Può anche essere usato nella sua forma differenziale totale, in cui hai
\[\displaystyle \Delta y \approx f'(x_0)(x-x_0)\]che ti dice una variazione approssimata in y, quando per un cambiamento in x (da \(x_0\) a \(x\)).
Il centro di tutte le calcolatrici algebriche inizia con la potenza dei numeri di base delle frazioni.
Esempio: calcolatrice differenziale
Considera la funzione: \(f(x) = x^2\). Trovare il suo differenziale nel punto \(x_0 = 1\).
Soluzione: Nel caso di questo primo esempio, lavoriamo con la funzione \(\displaystyle f(x)=x^2\), per la quale dobbiamo calcolare il suo differenziale nel punto \(x_0 = 1\).
La funzione è già stata semplificata, quindi possiamo procedere direttamente al calcolo della sua derivata:
Differenziale : La formula per il differenziale per la funzione \(\displaystyle f(x)=x^2\) nel punto \(x_0 = 1\) è:
\[dy = f'(x_0)(x - x_0) \]Definiamo \(\displaystyle y_0 = f(x_0)\), quindi inserire il valore del punto \(x_0 = 1\) nella funzione porta a:
\[y_0 = f(x_0) = f\left(1\right) = 1^2 = 1\]Inoltre, collegando il valore del punto \(x_0 = 1\) alla derivata calcolata si ottiene:
\[f'(x_0) = f'\left(1\right) = 2\cdot 1 = 2 \]Quindi, ora inseriamo questo valore nella formula differenziale per ottenere:
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = 2\left(x-1\right) \]\[\Rightarrow dy = 2x-2 \]Conclusione : Pertanto, troviamo che il differenziale per la funzione \(\displaystyle f(x)=x^2\) nel punto \(x_0 = 1\) è:
\[dy = 2x-2 \]Esempio: calcolo differenziale
Per la funzione data: \(f(x) = x^3 + 3x^2 - 2\), trovare il differenziale nel punto \(x_0 = 2\).
Soluzione: Ora, la funzione di cui abbiamo bisogno per trovare il differenziale è \(\displaystyle f(x)=x^3+3x^2-2\),
Calcolo Differenziale : Usiamo la seguente formula per il differenziale che dobbiamo costruire per la funzione data \(\displaystyle f(x)=x^3+3x^2-2\), nel punto dato \(x_0 = \frac{1}{2}\) è:
\[dy = f'(x_0)(x - x_0) \]Osserviamo che \(\displaystyle y_0 = f(x_0)\), il che significa che valutando la funzione in \(x_0 = \frac{1}{2}\) troviamo:
\[y_0 = f(x_0) = f\left(\frac{1}{2}\right) = \left(\frac{1}{2}\right)^3+3\left(\frac{1}{2}\right)^2-2 = -\frac{9}{8}\]Quindi, otteniamo la derivata nel punto \(x_0 = \frac{1}{2}\):
\[f'(x_0) = f'\left(\frac{1}{2}\right) = 3\left(\frac{1}{2}\right)^2+6\cdot \frac{1}{2} = \frac{15}{4} \]Di conseguenza, si ottiene quanto segue
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = \left(\frac{15}{4}\right)\left(x-\frac{1}{2}\right) \]\[\Rightarrow dy = \frac{15}{4}x-\frac{15}{8} \]Conclusione : La conclusione finale è che il differenziale che stiamo cercando è dato da:
\[dy = \frac{15}{4}x-\frac{15}{8} \]Esempio differenziale
Ci viene data la funzione: \(f(x) = \frac{\sin(x)}{x}\). Trovare il suo differenziale nel punto \(x_0 = \frac{\pi}{2}\).
Soluzione:
E' stata fornita la seguente funzione: \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), per la quale occorre calcolare il suo differenziale nel punto \(x_0 = \frac{\pi}{2}\).
La funzione è già stata semplificata, quindi possiamo procedere direttamente al calcolo della sua derivata:
Calcolo : Ora è il momento di trovare il differenziale associato a \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), per il dato punto \(x_0 = \frac{\pi}{2}\). La formula utilizzata è:
\[dy = f'(x_0)(x - x_0) \]Inseriamo il valore del punto \(x_0 = \frac{\pi}{2}\) nella derivata calcolata, che porta a:
\[f'(x_0) = f'\left(\frac{\pi}{2}\right) = \frac{\cos\left(\frac{\pi{}}{2}\right)}{\frac{\pi{}}{2}}-\frac{\sin\left(\frac{\pi{}}{2}\right)}{\left(\frac{\pi{}}{2}\right)^2} = -\frac{4}{\pi{}^2} \]Pertanto, utilizzando la formula differenziale:
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = \left(-\frac{4}{\pi{}^2}\right)\left(x-\frac{1}{2}\pi{}\right) \]\[\Rightarrow dy = \frac{2}{\pi{}}-\frac{4x}{\pi{}^2} \]Conclusione : Il differenziale corrispondente è:
\[dy = \frac{2}{\pi{}}-\frac{4x}{\pi{}^2} \]Altri calcolatori di differenziazione
trovare derivati è senza dubbio un elemento chiave in Calculus. I derivati forniscono le informazioni necessarie per comprendere il tasso di cambio di funzioni. poiché quelli hanno una connessione intima.
Fortunatamente, trovare le derivate è un processo sistematico (non necessariamente facile) se segui specifiche regole di differenziazione . Le regole più utilizzate sono le Regola Del Prodotto , Regola Del Quoziente e Regola Di Derivazione .
Lineare o approssimazioni del primo ordine tenta concettualmente di approssimare una funzione con una linea, almeno localmente, e può dirti molto sul comportamento di una funzione, vicino a un certo punto.






