Ulteriori informazioni sulle equazioni lineari

Questa calcolatrice ti aiuterà a rappresentare graficamente un'equazione lineare che fornisci. Quindi, il primo passo è fornire un'equazione lineare valida, qualcosa come 2x + 3y = 4, oppure potresti anche fornire qualcosa che non viene direttamente semplificato, come 2/3 x + y = 4/3 x - 1/ 2 y + 2. Qualsiasi espressione lineare valida funzionerà. .

Una volta fornita un'equazione lineare valida, arriva la parte facile, poiché tutto ciò che devi fare è fare clic su "Calcola" e ti verranno mostrati i passaggi del processo di rappresentazione grafica della funzione lineare.

Le equazioni lineari giocheranno un ruolo importante in molte operazioni, tra cui a risolvere un sistema di equazioni lineari .

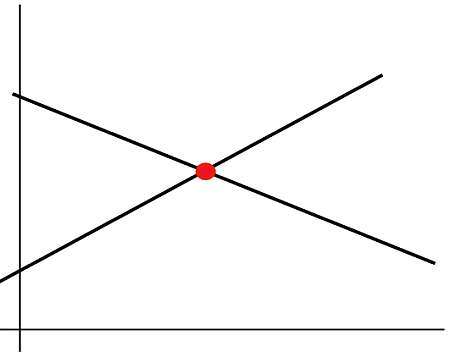
Formula di equazione lineare

Esistono diverse forme in cui è possibile scrivere una formula di equazione lineare. I più comuni sono i modulo standard , che è mostrato di seguito

\[a x + by = c \]

Inoltre, c'è il forma dell'intercetta della pendenza , che è mostrato di seguito

\[y = mx + n\]

Queste due forme possono essere per lo più convertite dall'una all'altra, salvo un paio di eccezioni, vale a dire la linea verticale espressa da x = a. Questa linea è verticale e attraversa l'asse x in (a, 0). Abbiamo che x = a è la forma standard della retta, ma questa retta non ha intercetta di pendenza (almeno dove y è la variabile dipendente)

Quali sono i passaggi per rappresentare graficamente un'equazione lineare?

• Passaggio 1: identificare chiaramente l'equazione disponibile
• Passaggio 2: guarda il coefficiente che moltiplica y, se è zero, allora hai una linea verticale
• Passaggio 3: se il coefficiente che moltiplica y è diverso da zero, allora risolvi per y per ottenere il forma dell'intercetta della pendenza
• Passaggio 4: utilizzando la forma dell'intercetta della pendenza, valuta la funzione in x = 0 e x = 1, quindi hai due punti in cui passa la linea
• Passaggio 5: traccia una linea usando quei due punti che hai trovato come guida

Uno dei modi più chiari per tracciare una linea è avere due punti in cui passa la linea, poiché spesso usare la pendenza come guida può essere fuorviante.

Soluzione di equazioni lineari in una variabile

Gli studenti hanno familiarità con i sistemi di equazioni lineari e comprendono più o meno ciò che deve essere fatto. Ma poi si interrogano sulla soluzione di un'equazione lineare in una variabile. Supponiamo di avere l'equazione lineare in forma di intercetta pendenza:

\[y = a + bx \]

Quindi, come lo risolvi? Bene, è già risolto: per ogni dato valore di x, la soluzione di y è y = a + bx. Quindi, ammesso che \(b \ne 0\), hai infinite soluzioni per un'equazione lineare.

La situazione cambia quando hai due equazioni lineari, nel qual caso è necessario risolvere entrambe le equazioni contemporaneamente .

Le equazioni lineari sono così importanti?

Scommetti! Forse tra i più importanti di tutta la matematica. Ciò è dovuto alla semplicità e alla vasta gamma di applicazioni.

Esempio: calcolatrice di equazioni lineari

Ottieni il grafico della seguente equazione lineare: \(\frac{1}{3} x + \frac{7}{4} y - \frac{5}{6} = 0\)

Soluzione:

Ottieni l'equazione della retta in forma di intercetta pendenza

Ci è stata data la seguente equazione:

\[\displaystyle \frac{1}{3}x+\frac{7}{4}y-\frac{5}{6}=0\]

Semplificando le costanti:

\[\displaystyle \frac{1}{3}x+\frac{7}{4}y-\frac{5}{6}=0\]

Ora, mettendo \(y\) a sinistra e \(x\) e la costante a destra otteniamo

\[\displaystyle \frac{7}{4}y = -\frac{1}{3}x + \frac{5}{6}\]

Ora, risolvendo per \(y\), dividendo entrambi i lati dell'equazione per \(\frac{7}{4}\), si ottiene quanto segue

\[\displaystyle y=-\frac{\frac{1}{3}}{\frac{7}{4}}x+\frac{\frac{5}{6}}{\frac{7}{4}}\]

e semplificando si ottiene la seguente formula

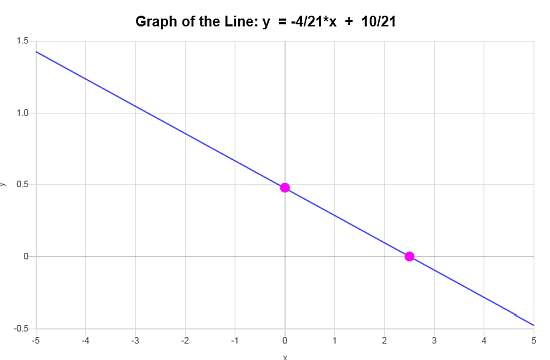
\[\displaystyle y=-\frac{4}{21}x+\frac{10}{21}\]

Conclusione : Deduciamo che l'equazione della retta in forma pendenza-intercetta basata sui dati disponibili è: \(\displaystyle y=-\frac{4}{21}x+\frac{10}{21}\), con pendenza \(\displaystyle b = -\frac{4}{21}\) e y-intercetta di \(\displaystyle n = \frac{10}{21}\).

Considerando questi dati, il grafico a linee fornito mostra

Esempio: esempio di calcolatrice di equazioni lineari

Calcola quanto segue: \(\frac{1}{3}x + \frac{5}{4}y = \frac{1}{6}\)

Soluzione: Ci è stata ora fornita la seguente equazione:

\[\displaystyle \frac{1}{3}x+\frac{5}{4}y=\frac{1}{6}\]

Il primo passo è semplificare le costanti:

\[\displaystyle \frac{1}{3}x+\frac{5}{4}y=\frac{1}{6}\]

Mettendo \(y\) a sinistra e \(x\) e il termine costante a destra otteniamo

\[\displaystyle \frac{5}{4}y = -\frac{1}{3}x +\frac{1}{6}\]

Ora, dobbiamo risolvere per \(y\), e ciò si ottiene dividendo entrambi i lati dell'equazione per \(\frac{5}{4}\), e si ottiene quanto segue

\[\displaystyle y=-\frac{\frac{1}{3}}{\frac{5}{4}}x+\frac{\frac{1}{6}}{\frac{5}{4}}\]

e semplificando si ottiene la seguente formula

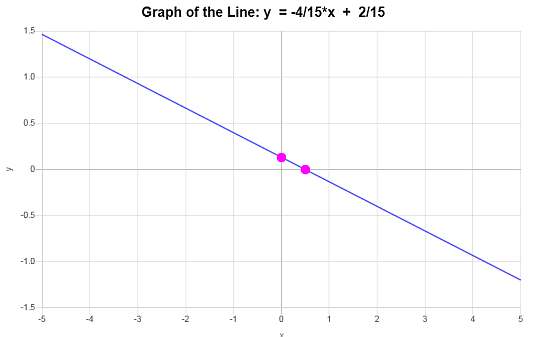
\[\displaystyle y=-\frac{4}{15}x+\frac{2}{15}\]

Conclusione : L'equazione della retta in forma di intercetta-pendenza è, secondo le informazioni fornite, \(\displaystyle y=-\frac{4}{15}x+\frac{2}{15}\), con pendenza di \(\displaystyle b = -\frac{4}{15}\) e intercetta sull'y di \(\displaystyle n = \frac{2}{15}\).

Secondo questi dati, il grafico a linee presentato è

Esempio: un altro esempio di calcolatrice di equazioni lineari

Questo rappresenta una linea: \( y = 5 \). Se sì, quali sono le sue caratteristiche?

Soluzione: Sì, lo fa. Infatti, quando si ha un'espressione come \( y = 5 \), si ha un'equazione lineare in forma di intercetta pendenza, con a = 0 e b = 5. Quindi, ciò che abbiamo è una linea orizzontale, che attraversa la y -asse nel punto (0, 5).

Altri calcolatori di algebra

Linee , Equazioni lineari e funzioni lineari giocherà sempre un ruolo cruciale in Algebra, presentando anche un chiaro legame con alcune proprietà geometriche di base.

In termini di applicazioni, forse Risoluzione di sistemi di equazioni lineari è tra le applicazioni più comuni di linee ed equazioni lineari.