Solveurs Algèbre

La règle des signes de descartes

Instructions: Utilisez cette calculatrice pour utiliser la règle des signes de Descartes pour les zéros des polynômes, en montrant toutes les étapes. Veuillez saisir le polynôme que vous devez analyser dans le champ de formulaire ci-dessous.

Utilisation de la règle des signes de descartes

Cette calculatrice vous aidera à appliquer la règle des signes de Descartes, pour tout polynôme donné que vous fournirez. La seule exigence est que le polynôme soit valide.

Par exemple, vous pouvez fournir un polynôme cubique simple comme x^3 - 2x + 1, mais vous pouvez également en fournir un plus compliqué, comme x^5 - 3/4 x^4 - 1/7 x^3 + 2 x^2 + 2x + 1, etc.

Une fois que vous avez fourni un fonction polynomiale vous cliquez sur le bouton "Calculer", afin d'afficher toutes les étapes du processus.

Trouver les zéros d'un polynôme est l'une des tâches les plus importantes en algèbre, mais ce n'est pas une tâche facile en général. Il n'existe pas de formules générales pour tous les polynômes de tous les degrés. Nous devons donc généralement suivre une procédure systématique pour trouver autant de racines que possible.

Dans ce contexte, il est toujours utile d'avoir le maximum d'informations sur le type de racines disponibles, et c'est l'un des objectifs de la règle des signes de Descartes.

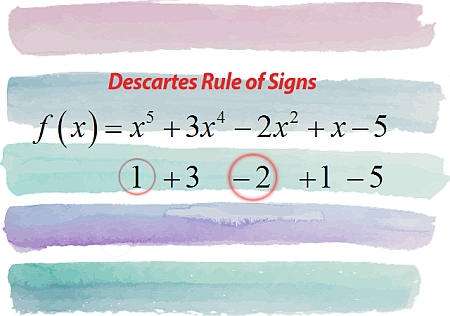
Que dit la règle des signes de descartes ?

En termes simples, la règle des signes de Descartes vous renseigne sur le nombre de racines positives et négatives d'un polynôme, en examinant simplement les signes des coefficients du polynôme en question.

Plus précisément, on commence par le coefficient de tête, et on ignore les coefficients nuls, et on va compter les changements de signe. Le nombre total de changements de signe de coefficients consécutifs est une limite supérieure pour le nombre de racines positives de $p(x)$, et la limite supérieure pour le nombre de racines positives de $p(x)$ nombre de racines positives a la même parité que le nombre total de changements de signes.

Ensuite, vous faites le même exercice, mais pour les coefficients de $p(-x)$, et ce que vous obtenez dans ce cas, c'est que le nombre total de changements de signe de coefficients consécutifs est une borne supérieure pour le nombre de racines négatives de $p(x)$, et le.. nombre de racines négatives a la même parité que le nombre total de changements de signe.

Étapes de l'application de la règle des signes de descartes

Étape 1: Identifiez le polynôme p(x) que vous devez analyser. Assurez-vous qu'il s'agit d'un polynôme (sinon la méthode ne fonctionne pas) et simplifiez-le autant que possible
Étape 2: Placez les coefficients de p(x) sur une ligne, en commençant par le premier coefficient, dans l'ordre décroissant et en omettant les coefficients nuls
Étape 3: En partant du premier coefficient, comptez les changements de signe entre les coefficients consécutifs, et notez le nombre total de changements de signe, que vous appellerez T
Étape 4: Le nombre de zéros positifs de p(x) est au plus égal à T et il a la même parité que T (si T est pair, alors le nombre de zéros positifs de p(x) est un nombre pair, et si T est impair, alors le nombre de zéros positifs de p(x) est un nombre impair)
Étape 4: Répétez le même processus pour les coefficients de p(-x), afin d'obtenir des informations sur le nombre de zéros négatifs de p(x)

Cette méthode peut vous donner potentiellement une gamme de valeurs possibles pour le nombre de zéros positifs (et négatifs), mais elle peut aussi potentiellement vous dire EXACTEMENT combien de zéros positifs (ou négatifs) un polynôme donné possède, en fonction uniquement du nombre de changements de signe que vous comptez.

Puis-je calculer les zéros réels avec cette méthode ?

Non, la règle des signes de Descartes n'est pas destinée à vous donner des informations sur ce que sont les racines réelles, elle vous indique seulement quelque chose sur le NOMBRE de racines positives (et négatives).

Maintenant, en combinant ces informations, avec les théorème de la racine rationnelle et d'autres outils élémentaires, notamment Division synthétique et le théorème des facteurs vous serez mieux armé pour examiner la valeur réelle des racines.

Conseils et astuces

Toujours simplifier le polynôme en premier. Par exemple, si vous avez $p(x) = x^5 - x^3$, vous voudrez d'abord à $p(x) = x^5 - x^3 = x^3(x^2 - 1)$, ainsi vous savez que 0 est une racine (avec multiplicité 3), et vous appliquez la règle de Descartes à $x^2 - 1$ à la place.

Calculatrice De La Règle Des Signes De Descartes

Exemple : la règle des signes de descartes

Indiquez le nombre possible de racines positives et négatives de $x^4 - x^3 + x^2 + 1$

Solution: On nous fournit la fonction polynomiale suivante : $\displaystyle x^4 - x^3 + x^2 + 1$, pour laquelle nous devons appliquer la règle des signes de Descartes.

Racines Positives : Les coefficients polynomiaux (de la puissance supérieure à la puissance inférieure) sont :

\[\,\,+1\,\, \,\,-1\,\, \,\,+1\,\, \,\,+1\,\,\]

Nous constatons que le nombre de changements de signe dans les coefficients consécutifs est : $2$, et les changements sont : $\,\,+1\,\,$ et$\,\,-1\,\,$, $\,\,-1\,\,$ et<$\,\,+1\,\,$.

Racines Négatives : Les coefficients polynomiaux pour $p(-x) = x^4+x^3+x^2+1$ sont :

\[\,\,+1\,\, \,\,+1\,\, \,\,+1\,\, \,\,+1\,\,\]

Aucun changement de signe n'est trouvé pour les coefficients de $p(-x)$.

Conclusion : En se basant sur le nombre de changements de signes trouvés, qui est $2$, on conclut que $p(x)$ peut avoir 0 ou 2 racines positives pour $p(x) = x^4-x^3+x^2+1$.

Maintenant, comme aucun changement de signe n'a été trouvé pour les coefficients de $p(-x)$, nous concluons qu'il n'y a PAS de zéros négatifs pour $p(x) = x^4-x^3+x^2+1$.

Exemple : plus de la règle du signe de descartes

Indiquez le nombre possible de racines positives et négatives de $x^4 + x^3 + x^2 - 1$

Solution: Maintenant, nous devons analyser $\displaystyle x^4 + x^3 + x^2 - 1$, avec la règle des signes de Descartes.

L'expression fournie est déjà simplifiée, il n'y a donc plus rien à simplifier.

Racines Positives : Les coefficients sont :

\[\,\,+1\,\, \,\,+1\,\, \,\,+1\,\, \,\,-1\,\,\]

Observez que le nombre de changements de signe dans les coefficients consécutifs dans ce cas est égal à $1$, et les changements sont : $\,\,+1\,\,$ et$\,\,-1\,\,$.

Racines Négatives : Les coefficients polynomiaux associés à $p(-x) = x^4-x^3+x^2-1$ sont :

\[\,\,+1\,\, \,\,-1\,\, \,\,+1\,\, \,\,-1\,\,\]

Ensuite, le nombre de changements de signe dans les coefficients consécutifs est égal à $3$, et les changements sont : $\,\,+1\,\,$ et $\,\,-1\,\,$, $\,\,-1\,\,$ et $\,\,+1\,\,$, $\,\,+1\,\,$ et<$\,\,-1\,\,$

Conclusion : Comme il y a un changement de signe parmi les coefficients de $p(x)$, on en conclut qu'il y a exactement UN zéro positif pour $p(x) = x^4+x^3+x^2-1$.

En se basant sur le nombre de changements de signes trouvés, qui est $3$, on conclut que $p(x) = x^4+x^3+x^2-1$ peut avoir 1 ou 3 racines négatives.

Exemple : signes positifs et négatifs

Indiquez le nombre possible de racines positives et négatives de $x^4 + 1$. Pouvez-vous dire quelque chose du nombre précis de racines positives et négatives ?

Solution: Dans ce cas, il n'y a pas de changement de signe, donc alors il n'y a pas de racines positives. Maintenant, $p(-x) = (-x)^4 + 1 = x^4 + 1$, qui n'a pas de changement de signe, donc alors il n'y a pas non plus de racines négatives. La conclusion est que le polynôme n'a pas de racines réelles (puisque 0 n'est pas non plus une racine).

Plus de calculateurs de polynômes

Trouver les racines d'un polynôme est l'un des points centraux de la plupart des problèmes d'application en calcul et en algèbre, et c'est une compétence qui mérite d'être maîtrisée.

Il y a de nombreuses compétences impliquées dans le calcul des zéros d'un polynôme, et Règle Des Signes De Descartes vous donne beaucoup d'informations qui peuvent être déduites simplement en regardant les coefficients du polynôme.