A propos de ce grapheur d'inégalité

Cette calculatrice vous aidera à trouver la solution et le graphique de n'importe quelle inégalité générale, en vous montrant toutes les étapes. Vous devez fournir une inégalité valide d'une variable (x), en la tapant dans la case prévue à cet effet.

Par exemple, vous pouvez fournir une simple inégalité linéaire comme "3x - 1 < 1/3", ou quelque chose comme "2x-x^2 <= 3/4", qui correspond à une inégalité quadratique.

Une fois que vous avez indiqué l'inégalité que vous souhaitez représenter graphiquement, cliquez sur le bouton "Solve", afin d'obtenir les solutions, avec toutes les étapes, au cas où il serait possible de trouver des solutions.

Résolution d'équations générales et les inégalités générales est en général une tâche difficile, sauf pour un ensemble spécifique de structures qui se prêtent à un traitement systématique.

Les quelques types qui permettent une solution exacte sont les suivants inégalités linéaires et inégalités polynomiales .

Un type important d'inégalités que vous aimerez résoudre est le cas des inégalités rationnelles, dans lesquelles vous pouvez identifier un quotient de polynômes. Ces inégalités sont intéressantes car elles comportent des divisions potentielles par zéro qui doivent être traitées. L'idée d'une inégalité rationnelle peut facilement être étendue au quotient de fonctions en général, pas nécessairement des polynômes

Comment représenter graphiquement une inégalité

La réponse la plus simple est la suivante : pour représenter graphiquement une inégalité, vous devez savoir comment la résoudre. La solution graphique d'une inégalité est généralement représentée sous la forme d'un intervalle ou de plusieurs intervalles joints sur l'axe des x.

Ceci étant dit, la représentation graphique d'une inégalité commence par sa résolution, ce qui implique de trouver un ensemble de valeurs sur la droite réelle qui satisfont l'inégalité fournie.

Vous pouvez potentiellement présenter le graphique comme un intervalle autonome, ou vous pouvez tracer les solutions de l'inégalité avec le graphique de l'expression qui sous-tend l'inégalité : rappelons que pour résoudre des inégalités vous passez tous les termes d'un côté (ce qui vous donne l'expression sous-jacente) et vous résolvez une équation auxiliaire

Étapes de la résolution et de la représentation graphique des inéquations

• Étape 1 : Passez tous les termes d'un côté, de sorte que vous ayez une expression d'un côté et zéro de l'autre
• Étape 2 : A partir de l'inégalité (une fois que tout est d'un côté et zéro de l'autre), construire une équation auxiliaire
• Étape 3 : Résoudre cette équation, avec une méthode adaptée à sa structure (différents types d'équations nécessiteront des techniques et des approches spécifiques)
• Étape 4 : Sur la base des solutions RÉELLES des équations auxiliaires (solutions réelles par opposition aux solutions complexes), vous construisez vos points critiques et les classez par ordre croissant
• Étape 5 : Vous devez également rechercher les points où l'expression est indéfinie. Un cas notable est celui des inégalités rationnelles, dans lesquelles le dénominateur est un polynôme, de sorte que l'expression est indéfinie sur les zéros du dénominateur. On ajoute donc les zéros du dénominateur à la liste des points critiques
• Étape 6 : Avec vos points critiques, vous construisez des intervalles en utilisant des points critiques consécutifs (en utilisant -∞ et ∞ comme points critiques de départ et d'arrivée)
• Étape 7 : Pour chaque intervalle, analysez le signe de l'expression et voyez s'il est compatible avec le signe de l'inégalité. Si c'est le cas, l'intervalle fera partie de la solution globale de l'inégalité

L'utilisation de points critiques pour l'analyse est de la plus haute importance, car cela permet de s'assurer que l'expression ne change pas de signe dans chaque intervalle, de sorte que le problème se réduit à évaluer si l'inégalité est résolue pour chacun de ces intervalles critiques.

Pour rendre la chose un peu plus tangible, vous avez une inégalité donnée, puis vous avez tout passé d'un côté, de sorte que vous avez quelque chose de la forme \(f(x) \le 0\). Par exemple, cela pourrait être quelque chose comme \(x^2 - x + 1 \le 0\).

On prend donc \(f(x) \le 0\) et on trouve l'équation auxiliaire \(f(x) = 0\). On prend l'expression \(f(x)\) et on trouve ses zéros qui sont les points critiques. Mais il faut aussi vérifier si \(f(x)\) n'est pas indéfinie quelque part (divisions par zéro, etc.). Elle peut être définie partout, comme dans le cas de \(x^2 - x + 1\), mais si vous trouvez des points où l'expression est indéfinie, vous l'ajoutez à la liste des points critiques.

Vous construisez ensuite des intervalles basés sur les points critiques consécutifs. Pour \(f(x) \le 0\), vous prendrez comme partie des solutions les intervalles où la valeur de l'expression est négative. Si l'inégalité originale aurait été \(f(x) \ge 0\), vous prendrez comme partie des solutions les intervalles où la valeur de l'expression est positive

Fonctionnement du grapheur d'inégalité

Notre calculatrice d'inégalité en ligne s'occupera de l'un des processus les plus fastidieux de l'algèbre de base, qui consiste à trouver les solutions d'une inégalité et à les représenter graphiquement. L'un des grands avantages de notre calculatrice est qu'elle affiche toutes les étapes, dans la mesure du possible.

Tout d'abord, le grapheur résoudra l'inégalité en résolvant d'abord une équation auxiliaire appropriée. Ce processus nécessite la détection de structures connues spécifiques, car toutes les structures requièrent probablement des approches différentes. Par exemple, pour résoudre une inégalité rationnelle (qui implique le quotient de deux polynômes) comme par exemple

\[\displaystyle \frac{x^2-2x}{x-1} \ge 4 \]

vous aurez besoin d'une approche différente de celle utilisée pour résoudre une inégalité quadratique comme \(x^2 + 3x < 1\), par exemple, et cette calculatrice prendra en charge tous ces détails

Si aucune structure traditionnelle ou connue n'est détectée, différentes substitutions courantes seront utilisées, comme par exemple \(u = \sqrt x\) ou \(u = \sin x\). Si rien ne fonctionne, la calculatrice tentera de trouver des solutions par inspection et numériquement, afin d'avoir au moins une idée des solutions...

Comment présenter un graphique d'inégalité ?

Comme nous l'avons mentionné plus haut, ce n'est pas vraiment gravé dans la pierre, mais la méthode la plus courante consiste à représenter graphiquement l'expression sous-jacente de l'inégalité et à mettre en évidence les valeurs x qui satisfont à l'inégalité. C'est probablement le meilleur format de graphique pour cela, et c'est ce qui est utilisé par ce graphiste.

Vous pouvez également dessiner un objet d'intervalle autonome, mais cette solution est peut-être moins parlante, car elle perd la perspective de ce qui se passe réellement avec l'inégalité elle-même.

Exemple : représentation graphique des inégalités

Représentez graphiquement l'inégalité suivante : \(\frac{1}{x}+x > 1\)

Solution : On nous donne l'inégalité suivante à résoudre :

\[\frac{1}{x}+x > 1\]

Nous devons mettre de côté tous les termes de l'inégalité :

\[x+\frac{1}{x}-1>0\]

Résolution de l'équation auxiliaire

À partir de l'inégalité ci-dessus, nous obtenons l'équation associée qui doit être résolue en premier lieu :

\[x+\frac{1}{x}-1=0\]

Analyse des points critiques

Nous devons classer les points critiques trouvés (à partir des racines réelles du numérateur et du dénominateur) par ordre croissant, définir des intervalles avec tous les points critiques consécutifs et évaluer le signe de la dimension gauche de l'inégalité sur chacun de ces intervalles.

Le seul point critique trouvé est \(0\).

Sur cette base, nous devons analyser les intervalles suivants :

- Pour l'intervalle \(\left(-\infty, 0\right)\) : Le numérateur est positif et le dénominateur est négatif, donc le côté gauche est négatif, ce qui implique que \(\left(-\infty, 0\right)\) ne fait pas partie de la solution.

- Pour l'intervalle \(\left(0, \infty\right)\) : Le numérateur est positif et le dénominateur est positif, donc le côté gauche est positif, donc \(\left(0, \infty\right)\) fait partie de la solution.

Solution à l'inégalité

En se basant sur l'inégalité fournie et en analysant les points critiques, on trouve que la solution de l'inégalité est : \(x > 0\).

En utilisant la notation par intervalles, la solution s'écrit comme suit :

\[\left(0,\infty\right)\]

Le graphique d'inégalité permet d'obtenir les résultats suivants :

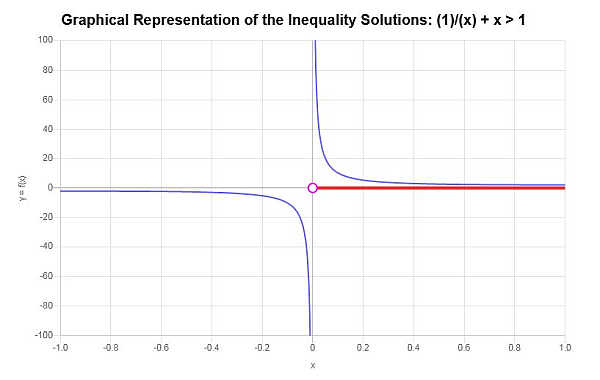
qui conclut le calcul.

Exemple : représentation graphique des inégalités polynomiales

Trouvez le graphique de l'inégalité : \(x^2 - 2x \ge 4\)

Solution :

Nous devons mettre de côté tous les termes de l'inégalité :

\[x^2-2x-4\ge0\]

Résolution de l'équation auxiliaire

À partir de l'inégalité ci-dessus, nous obtenons l'équation associée qui doit être résolue en premier lieu :

\[x^2-2x-4=0\]

Utilisation de la formule quadratique

Pour une équation quadratique de la forme \(a x^2 + bx + c = 0\), les racines sont calculées à l'aide de la formule suivante :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

Dans ce cas, l'équation à résoudre est \(\displaystyle x^2-2x-4 = 0\), ce qui implique que les coefficients correspondants sont :

\[a = 1\] \[b = -2\] \[c = -4\]

Tout d'abord, nous allons calculer le discriminant pour évaluer la nature des racines. Le discriminant est calculé comme suit :

\[\Delta = b^2 - 4ac = \displaystyle \left( -2\right)^2 - 4 \cdot \left(1\right)\cdot \left(-4\right) = 20\]

Puisque dans ce cas le discriminant est \(\Delta = \displaystyle 20 > 0\), qui est positif, nous savons que l'équation a deux racines réelles différentes.

En introduisant ces valeurs dans la formule des racines, nous obtenons :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(1\right)\left(-4\right)}}{2\cdot 1} = \displaystyle \frac{2 \pm \sqrt{20}}{2}\]

donc, nous trouvons que :

\[ {x}_1 = \frac{2}{2}-\frac{1}{2}\sqrt{20}=\frac{2}{2}-\sqrt{5}=1-\sqrt{5}=-\sqrt{5}+1 \] \[{x}_2 = \frac{2}{2}+\frac{1}{2}\sqrt{20}=\frac{2}{2}+\sqrt{5}=1+\sqrt{5}=\sqrt{5}+1\]

Dans ce cas, l'équation quadratique \( \displaystyle x^2-2x-4 = 0 \), a deux racines réelles, donc :

\[\displaystyle x^2-2x-4 = \left(x+\sqrt{5}-1\right)\left(x-\sqrt{5}-1\right)\]

alors le polynôme original est factorisé en \(\displaystyle p(x) = x^2-2x-4 = \left(x+\sqrt{5}-1\right)\left(x-\sqrt{5}-1\right) \), ce qui complète la factorisation.

Analyse des points critiques

La liste des points critiques trouvés, classés par ordre croissant, est la suivante : \(-\sqrt{5}+1\), \(\sqrt{5}+1\).

Sur cette base, nous devons analyser les intervalles suivants :

- Pour l'intervalle \(\left(-\infty, -\sqrt{5}+1\right)\) : Le côté gauche est positif, donc \(\left(-\infty, -\sqrt{5}+1\right)\) fait partie de la solution.

- Pour l'intervalle \(\left(-\sqrt{5}+1, \sqrt{5}+1\right)\) : Le côté gauche est négatif, donc \(\left(-\sqrt{5}+1, \sqrt{5}+1\right)\) ne fait pas partie de la solution.

- Pour l'intervalle \(\left(\sqrt{5}+1, \infty\right)\) : Le côté gauche est positif, ce qui implique que \(\left(\sqrt{5}+1, \infty\right)\) fait partie de la solution.

Solution à l'inégalité

En se basant sur l'inégalité fournie et en analysant les points critiques, on trouve que la solution de l'inégalité est : \(x \le -\sqrt{5}+1\) ou \(x \ge \sqrt{5}+1\).

En utilisant la notation par intervalles, la solution s'écrit comme suit :

\[\left(-\infty,-\sqrt{5}+1\right] \cup \left[\sqrt{5}+1,\infty\right)\]

Graphiquement :

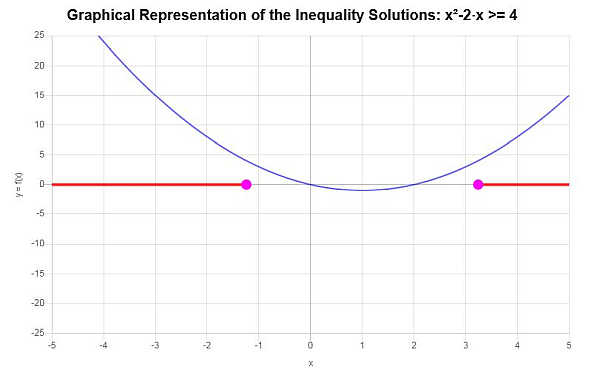
qui conclut le calcul.

Plus de calculatrices d'algèbre

Au fur et à mesure que vous progressez dans votre apprentissage de l'algèbre et du calcul, vous vous êtes probablement rendu compte que Résolution d'équations jouent un rôle crucial. Et au fur et à mesure que l'on apprend, on se rend compte que l'on dispose parfois de moins d'informations et que l'on se retrouve confronté à un problème de Résolution d'inéquations .

En fait, la résolution d'inéquations n'est pas plus difficile que la résolution d'équations, elle nécessite simplement quelques étapes plus organisées. Le principal problème est que nous ne pouvons pas vraiment résoudre la plupart des équations, du moins exactement.

Et même si nous résolvons des équations numériquement, nous n'avons pas encore de bons moyens de nous assurer que nous avons trouvé TOUTES les solutions à TOUTES les équations possibles. Certaines équations remarquables qui peuvent être résolues et qui apparaissent constamment dans les applications sont les suivantes équations polynomiales que vous pouvez résoudre en utilisant la plupart des méthodes standard (mais seulement pour les polynômes de degré inférieur)

Les inégalités rationnelles sont l'un des types d'inégalités les plus fréquemment demandés dans les tests de mathématiques, car il s'agit des inégalités simples les plus difficiles dont la solution est en quelque sorte garantie (à condition que les degrés impliqués soient suffisamment bas, ou que les polynômes soient suffisamment simples).