La ecuación del círculo
Un círculo es una de las figuras geométricas más notables. Tiene una simetría notable, basada en el hecho de que TODOS los puntos del círculo son equidistantes del centro, lo que en inglés significa que todos los puntos del círculo están a la misma distancia del centro. Esta distancia común \(r\) se llama radio del circulo .
El círculo tiene muchas aplicaciones geométricas importantes, lo que lo convierte en un objeto realmente importante tanto en geometría como en álgebra.
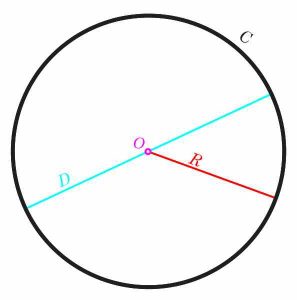
Otra propiedad crucial del círculo es que es muy fácil de representar algebraicamente. Esto significa que podemos establecer fácilmente una ecuación para representar todos los puntos en un círculo dado. Para decirlo más concretamente, considere el plano de coordenadas \(X - Y\). Todo esto significa que tenemos los ejes X e Y, que son perpendiculares entre sí.
Ecuacion del circulo
Ahora, hablemos de la ecuación que representa todos los puntos de un círculo dado. De hecho, para un círculo de radio \(r\), la siguiente ecuación describe los puntos \((x, y)\) que están en el círculo:
\[\Large x^2 + y^2 = r^2\]Lo anterior corresponde a la ecuación de una circunferencia de radio \(r\), con centro ubicado en \((0,0)\), origen de los ejes de coordenadas.
Cuando el radio es \(r = 1\), entonces tenemos lo que se llama un circulo unitario .
Al observar la ecuación anterior, la interpretación geométrica es que \(x\) y \(y\) son los lados de un triángulo y \(r\) es su hipotenusa
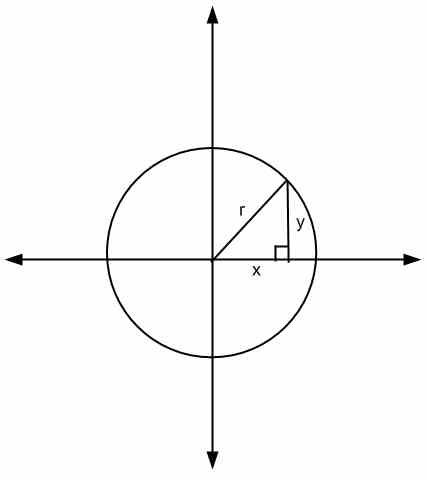
Otra forma de ver la ecuación del círculo es sacando raíces cuadradas a ambos lados de la ecuación, por lo que obtendríamos \(\sqrt{x^2+y^2} = r\), que indica que para cualquier punto \((x,y)\) del círculo, el distancia al origen (en este caso, el centro del círculo) es igual a \(r\).
Ecuación de un círculo que no está centrado en el origen
Una ventaja de trabajar en ejes coordinados es que los puntos en el círculo y el centro pueden ser situado en los ejes, y se puede representar mediante una ecuación, como se muestra arriba. Pero en general, el centro de la circunferencia no tiene por qué ser el origen, puede ser cualquier punto \((x_0, y_0\) en los ejes coordenados, en cuyo caso, la ecuación de la circunferencia se convierte en:
\[\Large (x-x_0)^2 + (y-y_0)^2 = r^2\]que se conoce como el Ecuación general de un círculo . Por ejemplo, digamos que necesita calcular la ecuación de un círculo de radio \(r = 4\), que está centrado en el punto \((1,2)\). Entonces, en este caso, tenemos \(x_0 = 1\), \(y_0 = 2\) y \(r = 4\), y luego reemplazamos estos números en la ecuación anterior y obtenemos
\[\large (x-1)^2 + (y-2)^2 = 4^2\]o también podemos escribir
\[\large (x-1)^2 + (y-2)^2 = 16\]Ejemplo 1
Escribe la ecuación de la circunferencia de radio 3, con centro en el origen. Usando la ecuación, determine si el punto (1, 2) pertenece o no al círculo.
Respuesta:
Primero, determinemos la ecuación del círculo. En este caso, el círculo está centrado en el origen, entonces \((x_0, y_0) = (0, 0)\). Por lo tanto, la ecuación es
\[\large x^2 + y^2 = 3^2\]que es lo mismo que
\[\large x^2 + y^2 = 9\]Ahora, la pregunta es si el punto (1, 2) está o no en el círculo. Sabemos que los puntos en el círculo serán tales que \(x^2 + y^2 = 9\).
Para el punto \((1, 2)\) obtenemos que \(x = 1\) y \(y=2\), entonces para este caso de ese punto, \(x^2 + y^2 = 1^2 + 2^2 = 1+ 4 = 5\) que es diferente de 9, y por lo tanto \((1,2)\) no pertenece al círculo.
Más sobre la ecuación del círculo
El círculo es una entidad matemática tan importante que se han escrito volúmenes de libros al respecto. Los círculos cruzan la geometría, la trigonometría y el álgebra, por eso es que tiene una apariencia transversal en todas partes en matemáticas.
¿cómo resolver la ecuación de un círculo?
Cuando trabajamos con un círculo, hay varias cosas que resolver. Lo primero es construir la ecuación de la circunferencia. Por ejemplo, considere un círculo de radio \(r = 3\), que está centrado en el punto \((1,1)\).
Basado en la ecuación general de un círculo, la ecuación es
\[\large (x-1)^2 + (y-1)^2 = 3^2\]La ecuación anterior se puede usar, por ejemplo, para determinar si un punto pertenece o no al círculo. ¿Qué más puedes hacer para resolver la ecuación del círculo? Potencialmente podría expandir los cuadrados, por lo que obtenemos
\[\large x^2 - 2x + 1 + y^2 -2y + 1 = 9\]que se puede simplificar en
\[\large x^2 - 2x + y^2 -2y = 7\]Entonces, ambas ecuaciones son equivalentes, en el sentido de que determinan el mismo círculo. ¿Cuál prefieres? \((x-1)^2 + (y-1)^2 = 3^2\) o \(x^2 - 2x + y^2 -2y = 7\)? Es cuestión de gustos y para qué usarías la fórmula.
Área de un círculo
Curiosamente, para calcular la área de un círculo , no necesitas la ecuación completa, solo necesitas saber el radio. En otras palabras, el área y circunferencia de un círculo no dependa de su centro.
¿la ecuación de un círculo es una función?
Esta es una pregunta que muchos estudiantes tienen y que debemos aclarar. En primer lugar, el ecuacion del circulo es una ecuación, no una relación o una función.
Ahora bien, la ecuación del círculo determina una relación, y no una función , cuando algebraicamente resolver para y en términos de x . De hecho, si resolvemos para \(y\) obtenemos:
\[\large x^2 + y^2 = 9 \Rightarrow y^2 = 9 - x^2 \] \[\large \Rightarrow y = \pm \sqrt{ 9 - x^2} \]Eso significa que para un \(x\) dado, hay dos valores de \(y\) que están asociados, que son \(\sqrt{ 9 - x^2}\) y \(-\sqrt{ 9 - x^2}\), lo que indica que la ecuación del círculo determina un relación en lugar de una función.
Un caso específico del círculo es el circulo unitario , con ecuación \(x^2 + y^2 = 1\), que está centrada en el origen. El círculo unitario es especialmente adecuado para trabajar con expresiones trigonométricas de una manera muy visual.
