Calculadora de residuos de regresión
Instrucciones: Utilice esta calculadora de residuos de regresión para encontrar los residuos de un análisis de regresión lineal para los datos independientes y dependientes proporcionados. Ingrese los datos para la variable independiente \((X)\) y la variable dependiente (\(Y\)), en el siguiente formulario:
Cómo calcular los residuos de regresión
Los residuos de la regresión corresponden a la diferencia entre los valores observados (\(y\)) y los valores pronosticados correspondientes (\(\hat y\)).
Ecuación residual de regresión
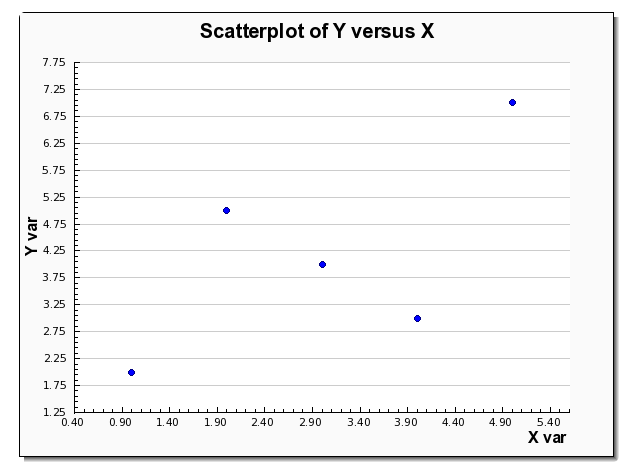
Al realizar un análisis de regresión lineal, el primer paso es hacer un diagrama de dispersión de los datos para X e Y que tiene disponibles, y si se observa un patrón lineal relativamente ajustado, puede realizar el análisis lineal de manera válida
Recordemos que si \(\hat \beta_0\) y \(\hat \beta_1\) son la intersección y la pendiente estimadas correspondientes, respectivamente, entonces el valor pronosticado (\(\hat y\)) para un valor dado \(x\) es
\[ \hat y = \hat \beta_0 + \hat \beta_1 x \]Luego, el residual asociado al par \((x,y)\) se define utilizando la siguiente ecuación estadística residual:
\[ \text{Residual} = y - \hat y \]El residual representa qué tan lejos está la predicción del valor real observado. Esto significa que nos gustaría tener residuos lo más pequeños posible.
De hecho, la idea detrás de los mínimos cuadrados Regresión lineal es encontrar los parámetros de regresión basados en aquellos que minimizarán la suma de los residuos al cuadrado.

Cómo encontrar los residuos para una regresión
- Recopile los datos de muestra para X e Y
- Realice un análisis de regresión lineal y encuentre la ecuación de regresión \(\hat y = \hat \beta_0 + \hat \beta_1 x\)
- Para cada punto de muestra \(x_i\) y \(y_i\), calcule el residuo usando la fórmula: \(\text{Residual} = y_i - \hat y_i \)
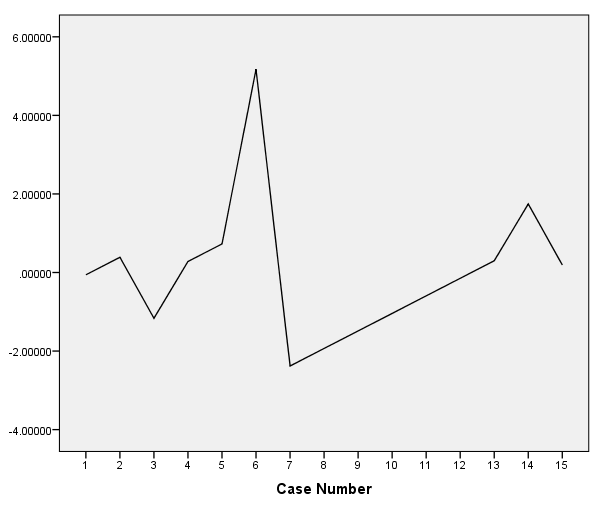
- Una vez que tenga todos los puntos residuales, puede graficarlos de diferentes maneras para evaluar la calidad y las propiedades del modelo estimado.
- Calcular residuos es importante porque proporciona una forma gráfica de evaluar la plausibilidad de los supuestos de regresión.
- Para que los resultados de la regresión sean confiables, espera que los residuos tengan al menos una distribución de probabilidad normal .
¿qué hace esta calculadora residual?
Lo que hará esta calculadora residual es tomar los datos que ha proporcionado para X e Y y calculará el modelo de regresión lineal, paso a paso.
Luego, para cada valor de los datos de la muestra, se calculará el valor pronosticado correspondiente, y este valor se restará de los valores observados y, para obtener los residuos.
Todo esto se tabulará y se le presentará claramente. Además, un diagrama de dispersión de residuos versus valores predictivos se presentará. Esta gráfica residual es crucial para evaluar si se cumplen o no los supuestos del modelo de regresión lineal.
¿qué más puedes hacer con estos datos?
Por lo general, un paso inicial para realizar un análisis de regresión lineal es realizar un análisis correlacional. Puedes usar nuestro calculadora de coeficiente de correlación para encontrar el coeficiente de correlación, que indica el grado de asociación entre las dos variables.
El cálculo del coeficiente de correlación suele ir acompañado de la construcción de un diagrama de dispersión. Usando un diagrama de dispersión y el coeficiente de correlación, podemos decidir si es apropiado o no realizar un análisis de regresión lineal, especialmente si descubrimos usando este calculadora de significado del coeficiente de correlación , que la correlación es significativamente diferente de cero.