Más sobre estadísticas descriptivas: uso de esta calculadora de medias

La estadística descriptiva corresponde a medidas y gráficos que se derivan de Data de muestra y están destinados a proporcionar información sobre la población que se está estudiando. Dos tipos básicos de estadísticas descriptivas son las medidas de tendencia central y el medidas de dispersión .

¿cómo calcular la media?

Para calcular la media de la muestra, debe usar la siguiente fórmula:

\[ \bar X = \displaystyle \frac{1}{n} \sum_{i=1}^n X_i \]

En términos simples, divide la suma de todos los valores de la muestra por el número total de valores de la muestra.

Cómo usar esta calculadora de media

Para calcular la media de una muestra, debe seguir estos pasos:

• Paso 1 : Identifique claramente la muestra que desea analizar y calcule la media, y asegúrese de que todos los valores sean numéricos; de lo contrario, no podrá continuar.
• Paso 2 : Si solo está calculando la media, entonces no necesita ordenar los datos. pero si tu tambien quieres calcular la mediana y percentiles , deberá ordenar los datos en orden ascendente
• Paso 3 : Calcule el número de valores en la muestra n, también conocido como el tamaño de la muestra, y calcule el suma de la muestra
• Paso 4 : La media de la muestra se calcula dividiendo la suma de los datos por el tamaño de la muestra

Entonces, para encontrar la media, solo necesita calcular el promedio de los datos.

La media es una de las medidas de tendencia central más utilizadas, y por una buena razón. Sabemos que para un tamaño de muestra suficientemente grande, la media de la muestra será numéricamente cercana a la media de la población.

En términos técnicos (te perdí ahí, lo sé), la media de la muestra es una estimación puntual imparcial de la media de la población.

Este Calculadora media le mostrará todos los pasos del proceso y todo lo que necesita hacer es escribir o pegar desde Excel los datos de muestra con los que desea trabajar.

Además de eso, también obtiene los pasos para calcular la desviación estándar, lo que le brinda una buena imagen de las estadísticas descriptivas más importantes que necesita para comenzar.

Medidas de tendencia central

Las medidas de tendencia central pretenden dar una idea de la ubicación de la distribución. Ejemplos de medidas de tendencia central son la muestra promedio \(\bar X\), el mediana y el modo.

Observe que la media de la muestra es la misma que el promedio de los datos. Sin embargo, en el contexto de las estadísticas, el nombre más utilizado es media muestral.

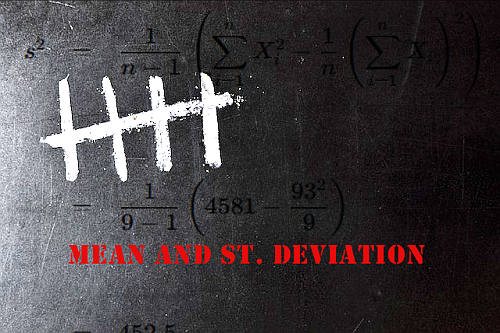
Medidas de dispersión

Ejemplos de medidas de dispersión son la varianza \(s^2\), la desviación estándar \(s\) y el rango entre otras. Diferentes medidas son más apropiadas que otras para ciertos casos.

Por ejemplo, ciertas medidas como la media son muy sensibles a valores atípicos , y por lo tanto, cuando una muestra tiene fuertes valores atípicos o está muy sesgada, la medida de tendencia central preferida sería la mediana en lugar de la media muestral.

Si desea realizar un análisis más completo y exhaustivo, utilice nuestro calculadora de estadísticas descriptivas .

Propiedades de la media y desviación estándar

Una excelente propiedad de la media muestral es que es un estimador insesgado de la media poblacional, y que tiene la propiedad de que si elegimos un tamaño de muestra relativamente grande, sabemos que el valor numérico de la media muestral obtenida es cercano a la media poblacional real.

La desviación estándar de la muestra, por otro lado, no es una estimación imparcial de la desviación estándar de la población, pero aún así, el valor numérico de la desviación estándar de la muestra estará cerca de la verdadera desviación estándar de la población para un tamaño de muestra grande.

Otro tipo de medios

La media de la muestra, que se basa en el promedio de los datos de la muestra, no es el único tipo de "media" que puede concebir, ya que también puede calcular la significado armónico y el significado geométrico , que también intentan encontrar un elemento representativo de una muestra, pero utilizando un enfoque numérico diferente.

Encontrar un valor representativo de una muestra realmente depende de la forma de la distribución. Para distribuciones sesgadas será mejor calculando la mediana o el forma , ya que las distribuciones sesgadas tenderán a sobrerrepresentar la cola sesgada al calcular la media.